
С Днем космонавтики! Мы отправили его в типографию «Маленькая книга черных дыр» .
Именно в эти дни астрофизики показали всему миру, как выглядят черные дыры.
Совпадение? Мы так не думаем ;) Так что ждите, скоро появится потрясающая книга, написанная Стивеном Габсером и Франсом Преториусом, в переводе замечательного пулковского астронома ака Астродада Кирилла Масленникова, под научной редакцией легендарного Владимира Сурдина и при поддержке ее публикации Фонд «Траектория».
Отрывок «Термодинамика черных дыр» под катом.
До сих пор мы рассматривали черные дыры как астрофизические объекты, образовавшиеся во время взрывов сверхновых или лежащие в центрах галактик.
Мы наблюдаем их косвенно, измеряя ускорения близких к ним звезд. Знаменитое обнаружение гравитационных волн LIGO 14 сентября 2015 года стало примером более прямых наблюдений столкновений черных дыр.
Математические инструменты, которые мы используем, чтобы лучше понять природу черных дыр, включают: дифференциальную геометрию, уравнения Эйнштейна, а также мощные аналитические и численные методы, используемые для решения уравнений Эйнштейна и описания геометрии пространства-времени, которую генерируют черные дыры.
И как только мы сможем дать полное количественное описание пространства-времени, порождаемого черной дырой, с астрофизической точки зрения тему черных дыр можно считать закрытой.
С более широкой теоретической точки зрения остается еще много возможностей для исследований.
Цель этой главы — осветить некоторые теоретические достижения современной физики черных дыр, в которой идеи термодинамики и квантовой теории сочетаются с общей теорией относительности, порождая неожиданные новые концепции.
Основная идея заключается в том, что черные дыры — это не просто геометрические объекты.
У них есть температура, огромная энтропия, и они могут демонстрировать проявления квантовой запутанности.
Наши рассуждения о термодинамических и квантовых аспектах физики черных дыр будут более фрагментарными и поверхностными, чем анализ чисто геометрических особенностей пространства-времени в черных дырах, представленный в предыдущих главах.
Но эти, и особенно квантовые, аспекты являются существенной и жизненно важной частью продолжающихся теоретических исследований черных дыр, и мы очень постараемся передать если не сложные детали, то, по крайней мере, дух этих работ. В классической общей теории относительности — если говорить о дифференциальной геометрии решений уравнений Эйнштейна — черные дыры действительно черные в том смысле, что из них ничто не может ускользнуть.
Стивен Хокинг показал, что эта ситуация полностью меняется, если мы принимаем во внимание квантовые эффекты: черные дыры излучают излучение при определенной температуре, известной как температура Хокинга.
Для черных дыр астрофизических размеров (то есть от звездной массы до сверхмассивных черных дыр) температура Хокинга ничтожно мала по сравнению с температурой космического микроволнового фона — излучения, заполняющего всю Вселенную, которое, кстати, может само по себе можно считать вариантом излучения Хокинга.
Расчеты Хокинга по определению температуры черных дыр являются частью более крупной исследовательской программы в области, называемой термодинамикой черных дыр.
Другая важная часть этой программы — исследование энтропии черной дыры, которое измеряет количество информации, теряемой внутри черной дыры.
Обычные объекты (такие как кружка с водой, блок чистого магния или звезда) также обладают энтропией, и одно из центральных утверждений термодинамики черной дыры заключается в том, что черная дыра заданного размера имеет больше энтропии, чем любая другая форма.
материи, которая может содержаться внутри.
область такого же размера, но без образования черной дыры.
Но прежде чем мы углубимся в вопросы, связанные с излучением Хокинга и энтропией черной дыры, давайте совершим небольшой экскурс в области квантовой механики, термодинамики и запутанности.
Квантовая механика была разработана в основном в 1920-х годах, и ее основной целью было описание очень маленьких частиц материи, таких как атомы.
Развитие квантовой механики привело к размыванию таких основных понятий физики, как точное положение отдельной частицы: оказалось, например, что положение электрона при его движении вокруг атомного ядра не может быть точно определено.
Вместо этого электронам были назначены так называемые орбиты, на которых их фактическое положение можно определить только в вероятностном смысле.
Однако для наших целей важно не слишком быстро переходить к вероятностной стороне дела.
Возьмем самый простой пример: атом водорода.
Он может находиться в определенном квантовом состоянии.
Простейшее состояние атома водорода, называемое основным состоянием, — это состояние с наименьшей энергией, и эта энергия точно известна.
В более общем смысле, квантовая механика позволяет нам (в принципе) знать состояние любой квантовой системы с абсолютной точностью.
Вероятности вступают в игру, когда мы задаем определенные вопросы о квантово-механической системе.
Например, если точно известно, что атом водорода находится в основном состоянии, мы можем спросить: «Где находится электронЭ» и по законам квантовой
механики, мы получим лишь некоторую оценку вероятности для этого вопроса, примерно что-то вроде: «вероятно, электрон находится на расстоянии до половины ангстрема от ядра атома водорода» (один ангстрем равен 
метров).
Но у нас есть возможность посредством определенного физического процесса найти положение электрона гораздо точнее, чем с точностью до одного ангстрема.
Этот довольно распространенный в физике процесс включает в себя попадание фотона очень короткой длины волны в электрон (или, как говорят физики, рассеяние фотона на электроне) - после чего мы можем с точностью восстановить местоположение электрона в момент рассеяния приблизительно равна длине волны фотона.
Но этот процесс изменит состояние электрона, так что после этого он уже не будет находиться в основном состоянии атома водорода и не будет иметь точно определенной энергии.
Но в течение некоторого времени его положение будет почти точно определено (с точностью до длины волны используемого для этого фотона).
Предварительную оценку положения электрона можно сделать только в вероятностном смысле с точностью около одного ангстрема, но как только мы его измерим, мы точно узнаем, что это было.
Короче говоря, если мы каким-то образом измеряем квантовомеханическую систему, то, по крайней мере в общепринятом смысле, мы «принуждаем» ее привести в состояние с определенным значением измеряемой нами величины.
Квантовая механика применима не только к малым системам, но (как мы полагаем) ко всем системам, но для больших систем правила квантовой механики быстро становятся очень сложными.
Ключевой концепцией является квантовая запутанность, простым примером которой является концепция спина.
Отдельные электроны имеют спин, поэтому на практике один электрон может иметь спин, направленный вверх или вниз относительно выбранной пространственной оси.
Спин электрона является наблюдаемой величиной, поскольку электрон генерирует слабое магнитное поле, подобное полю магнитного стержня.
Тогда вращение вверх означает, что северный полюс электрона направлен вниз, а вращение вниз означает, что северный полюс направлен вверх.
Два электрона можно поместить в сопряженное квантовое состояние, в котором один из них имеет спин вверх, а другой — вниз, но невозможно сказать, какой электрон имеет какой спин.
По сути, в основном состоянии атома гелия два электрона находятся именно в таком состоянии, называемом спиновым синглетом, поскольку суммарный спин обоих электронов равен нулю.
Если мы разделим эти два электрона, не меняя их спинов, мы все равно сможем сказать, что они вместе являются синглетами спина, но мы все равно не сможем сказать, каким будет спин каждого из них по отдельности.
Теперь, если мы измерим один из их спинов и установим, что он направлен вверх, то мы будем полностью уверены, что второй направлен вниз.
В этой ситуации мы говорим, что спины запутаны: ни один из них сам по себе не имеет определенного значения, а вместе они находятся в определенном квантовом состоянии.
Эйнштейна очень беспокоило явление запутанности: оно, казалось, угрожало основным принципам теории относительности.
Рассмотрим случай двух электронов в спин-синглетном состоянии, когда они находятся далеко друг от друга в пространстве.
Для уверенности пусть Алиса возьмет один из них, а Боб — другой.
Допустим, Алиса измерила спин своего электрона и обнаружила, что он направлен вверх, а Боб ничего не измерял.
Пока Алиса не провела измерение, было невозможно определить спин его электрона.
Но как только она завершила свое измерение, она абсолютно точно знала, что спин электрона Боба направлен вниз (в сторону, противоположную спине ее собственного электрона).
Означает ли это, что ее измерение мгновенно перевело электрон Боба в состояние со спином вниз? Как это могло произойти, если электроны пространственно разделены? Эйнштейн и его сотрудники Натан Розен и Борис Подольский считали, что история измерения запутанных систем настолько серьезна, что ставит под угрозу само существование квантовой механики.
Сформулированный ими парадокс Эйнштейна-Подольского-Розена (ЭPR) использует мысленный эксперимент, подобный тому, который мы только что описали, чтобы прийти к выводу, что квантовая механика не может быть полным описанием реальности.
Теперь, на основе последующих теоретических исследований и многих измерений, установлено общее мнение, что парадокс ЭPR содержит ошибку, а квантовая теория верна.
Квантово-механическая запутанность реальна: измерения запутанных систем будут коррелировать, даже если системы находятся далеко друг от друга в пространстве-времени.
Давайте вернемся к ситуации, когда мы поместили два электрона в спин-синглетное состояние и передали их Алисе и Бобу.
Что мы можем сказать об электронах до проведения измерений? Что они оба вместе находятся в определенном квантовом состоянии (спин-синглет).
Вращение электрона Алисы с равной вероятностью будет направлено вверх или вниз.
Точнее, квантовое состояние его электрона может с равной вероятностью быть одним (спин вверх) или другим (спин вниз).
Теперь для нас понятие вероятности приобретает более глубокий смысл, чем раньше.
Ранее мы рассмотрели определенное квантовое состояние (основное состояние атома водорода) и увидели, что существуют некоторые «неудобные» вопросы, например: «Где находится электронЭ» - вопросы, на которые ответы существуют только в вероятностном смысле.
Если бы мы задали «хорошие» вопросы, например: «Какова энергия этого электронаЭ», мы бы получили однозначные ответы.
Теперь не существует «хороших» вопросов, которые мы могли бы задать об электроне Алисы, на которые не было бы ответов, зависящих от электрона Боба.
(Мы не говорим о глупых вопросах типа «Есть ли у электрона Алисы спинЭ» — вопросах, на которые есть только один ответ.) Итак, для определения параметров одной половины запутанной системы нам придется воспользоваться вероятностный язык.
Уверенность возникает только тогда, когда мы рассматриваем связь между вопросами, которые Алиса и Боб могут задать о своих электронах.
Мы намеренно начали с одной из самых простых известных нам квантовомеханических систем: системы спинов отдельных электронов.
Есть надежда, что на основе таких простых систем будут построены квантовые компьютеры.
Спиновую систему отдельных электронов или другие эквивалентные квантовые системы теперь называют кубитами (сокращение от «квантовые биты»), подчеркивая их роль в квантовых компьютерах, аналогичную роли, которую играют обычные биты в цифровых компьютерах.
Давайте теперь представим, что мы заменили каждый электрон гораздо более сложной квантовой системой со многими, а не только двумя квантовыми состояниями.
Например, они давали Алисе и Бобу батончики чистого магния.
Прежде чем Алиса и Боб разойдутся, их бруски могут взаимодействовать, и мы согласны, что при этом они приобретают определенное общее квантовое состояние.
Как только Алиса и Боб расстаются, их магниевые стержни перестают взаимодействовать.
Как и в случае с электронами, каждый стержень находится в неопределенном квантовом состоянии, хотя вместе, как мы полагаем, они образуют вполне определенное состояние.
(В этом обсуждении мы предполагаем, что Алиса и Боб способны перемещать свои магниевые стержни, никоим образом не нарушая их внутреннего состояния, точно так же, как мы ранее предполагали, что Алиса и Боб могут разделить свои запутанные электроны, не меняя их спинов.
) Но есть Разница Разница между этим мысленным экспериментом и электронным экспериментом заключается в том, что неопределенность квантового состояния каждого стержня огромна.
Столбец вполне может приобрести больше квантовых состояний, чем число атомов во Вселенной.
Здесь в игру вступает термодинамика.
Тем не менее очень плохо определенные системы могут иметь некоторые четко определенные макроскопические характеристики.
Такой характеристикой является, например, температура.
Температура является мерой того, насколько вероятно, что какая-либо часть системы будет иметь определенную среднюю энергию, при этом более высокие температуры соответствуют большей вероятности наличия большей энергии.
Другой термодинамический параметр — энтропия, которая по существу равна логарифму числа состояний, которые может принять система.
Другой термодинамической характеристикой, которая была бы важна для магниевого стержня, является его чистая намагниченность, которая, по сути, является параметром, показывающим, насколько больше в стержне электронов со спином вверх, чем электронов со спином вниз.
Мы включили в наш рассказ термодинамику как способ описания систем, квантовые состояния которых точно не известны из-за их запутанности с другими системами.
Термодинамика — мощный инструмент анализа таких систем, но ее создатели совершенно не предполагали ее применения таким образом.
Сади Карно, Джеймс Джоуль, Рудольф Клаузиус были деятелями промышленной революции XIX века, и их интересовал самый практический из всех вопросов: как работают двигатели? Давление, объем, температура и тепло — это плоть и кровь двигателей.
Карно установил, что энергия в форме тепла никогда не может быть полностью преобразована в полезную работу, например, при подъеме грузов.
Часть энергии всегда будет потрачена впустую.
Клаузиус внес крупный вклад в создание идеи энтропии как универсального инструмента для определения потерь энергии во время любого процесса, связанного с выделением тепла.
Его главным достижением было осознание того, что энтропия никогда не уменьшается — почти во всех процессах она возрастает. Процессы, при которых энтропия возрастает, называются необратимыми именно потому, что их нельзя обратить вспять без уменьшения энтропии.
Следующий шаг к развитию статистической механики сделали Клаузиус, Максвелл и Людвиг Больцман (среди многих других) — они показали, что энтропия является мерой беспорядка.
Обычно, чем больше вы что-то предпринимаете, тем больше беспорядка вы создаете.
И даже если вы спроектируете процесс, целью которого является восстановление порядка, он неизбежно создаст больше энтропии, чем будет уничтожено — например, за счет выделения тепла.
Кран, укладывающий стальные балки в идеальном порядке, создает порядок в расположении балок, но при работе он выделяет столько тепла, что общая энтропия все равно возрастает. Но все же разница между взглядом на термодинамику физиков XIX века и взглядом, связанным с квантовой запутанностью, не так велика, как кажется.
Каждый раз, когда система взаимодействует с внешним агентом, ее квантовое состояние переплетается с квантовым состоянием агента.
Обычно такая запутанность приводит к увеличению неопределенности квантового состояния системы, иными словами, к увеличению числа квантовых состояний, в которых может находиться система.
В результате взаимодействия с другими системами энтропия, определяемая количеством квантовых состояний, доступных системе, обычно увеличивается.
В целом квантовая механика обеспечивает новый способ характеристики физических систем, в котором некоторые параметры (например, положение в пространстве) становятся неопределенными, но другие (например, энергия) часто известны с уверенностью.
В случае квантовой запутанности две принципиально отдельные части системы имеют известное общее квантовое состояние, а каждая часть в отдельности имеет неопределенное состояние.
Стандартный пример запутанности — пара спинов в синглетном состоянии, в котором невозможно определить, какой спин верхний, а какой нижний.
Неопределенность квантового состояния в большой системе требует термодинамического подхода, при котором макроскопические параметры, такие как температура и энтропия, известны с большой точностью, даже если система имеет множество возможных микроскопических квантовых состояний.
Завершив наш краткий экскурс в области квантовой механики, запутанности и термодинамики, попробуем теперь понять, как все это приводит к пониманию того факта, что черные дыры имеют температуру.
Первый шаг к этому сделал Билл Унру — он показал, что ускоряющийся наблюдатель в плоском пространстве будет иметь температуру, равную его ускорению, делённому на 2π.
Ключом к расчетам Унру является то, что наблюдатель, движущийся с постоянным ускорением в определенном направлении, может видеть только половину плоского пространства-времени.
Вторая половина по сути находится за горизонтом, похожим на горизонт черной дыры.
На первый взгляд это кажется невозможным: как может плоское пространство-время вести себя как горизонт черной дыры? Чтобы понять, чем это обернется, давайте обратимся за помощью к нашим верным наблюдателям Алисе, Бобу и Биллу.
По нашей просьбе они выстраиваются в шеренгу, Алиса находится между Бобом и Биллом, а расстояние между наблюдателями в каждой паре составляет ровно 6 километров.
Мы договорились, что в нулевой момент времени Алиса прыгнет в ракету и полетит к Биллу (и, следовательно, от Боба) с постоянным ускорением.
Ее ракета очень хороша, способна развивать ускорение, в 1,5 триллиона раз превышающее гравитационное ускорение, с которым движутся объекты у поверхности Земли.
Конечно, Алисе нелегко выдержать такое ускорение, но, как мы сейчас увидим, эти числа выбраны неслучайно; в конце концов, мы просто обсуждаем потенциальные возможности, вот и все.
Ровно в тот момент, когда Алиса прыгает в свою ракету, Боб и Билл машут ей рукой.
(Мы имеем право использовать выражение «именно в тот момент, когда…», потому что, хотя Алиса еще не начала свой полет, она находится в той же системе отсчета, что и Боб и Билл, поэтому они все могут синхронизировать свои часы .
) Маша Алиса, конечно, видит к себе Билла: однако, находясь в ракете, она увидит его раньше, чем это произошло бы, если бы она осталась там, где была, потому что ее ракета с ней летит именно к нему.
Напротив, она отдаляется от Боба, поэтому мы можем обоснованно предположить, что она увидит, как он машет ей рукой, несколько позже, чем увидела бы, если бы осталась на том же месте.
Но правда еще удивительнее: она вообще не увидит Боба! Другими словами, фотоны, которые летят из машущей руки Боба к Алисе, никогда ее не догонят, даже учитывая, что она никогда не сможет достичь скорости света.
Если бы Боб начал махать рукой, находясь чуть ближе к Алисе, то фотоны, улетевшие от него в момент ее ухода, догнали бы ее, а если бы он был чуть дальше, они бы ее не догнали.
Именно в этом смысле мы говорим, что Алиса видит только половину пространства-времени.
В тот момент, когда Алиса начинает двигаться, Боб находится чуть дальше за горизонтом, наблюдая за происходящим.
Обсуждая квантовую запутанность, мы привыкли к идее, что даже если квантовомеханическая система в целом имеет определенное квантовое состояние, некоторые ее части могут его не иметь.
Фактически, когда мы обсуждаем сложную квантовую систему, некоторую ее часть лучше всего можно охарактеризовать именно с точки зрения термодинамики: ей можно приписать четко определенную температуру, несмотря на весьма неопределенное квантовое состояние всей системы.
Наша последняя история с участием Алисы, Боба и Билла немного похожа на эту ситуацию, но квантовая система, о которой мы здесь говорим, представляет собой пустое пространство-время, и Алиса видит только половину его.
Оговоримся, что пространство-время в целом находится в основном состоянии, а значит, в нем нет частиц (конечно, не считая Алисы, Боба, Билла и ракеты).
Но та часть пространства-времени, которую видит Алиса, будет находиться не в основном состоянии, а в состоянии, запутанном с той его частью, которую она не видит. Пространство-время, воспринимаемое Алисой, находится в сложном, неопределенном квантовом состоянии, характеризующемся конечной температурой.
Расчеты Унру показывают, что эта температура составляет примерно 60 нанокельвинов.
Короче говоря, когда Алиса ускоряется, она как бы погружается в теплую ванну излучения с температурой, равной (в соответствующих единицах) ускорению, делённому на 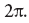

Рис.
7.1. Алиса движется с ускорением из состояния покоя, а Боб и Билл остаются неподвижными.
Ускорение Алисы таково, что она никогда не увидит фотонов, которые Боб посылает ей в момент t = 0. Однако она получает фотоны, которые Билл послал ей в момент t = 0. В результате Алиса может наблюдать только половину пространство-время.
Странность расчетов Унру заключается в том, что, хотя они от начала до конца относятся к пустому пространству, они противоречат знаменитым словам короля Лира: «Из ничего не возникает ничего».
Как пустое пространство может быть таким сложным? Откуда могут взяться частицы? Дело в том, что согласно квантовой теории пустое пространство вовсе не пусто.
В нем то тут, то там постоянно появляются и исчезают кратковременные возбуждения, называемые виртуальными частицами, энергия которых может быть как положительной, так и отрицательной.
Наблюдатель из далекого будущего — назовем ее Кэрол, — который может видеть почти все пустое пространство, может подтвердить, что в нем нет долгоживущих частиц.
Более того, наличие частиц с положительной энергией в той части пространства-времени, которую может наблюдать Алиса, вследствие квантовой запутанности связано с возбуждениями равного и противоположного знака энергии в ненаблюдаемой для Алисы части пространства-времени.
Кэрол открывается вся правда о пустом пространстве-времени в целом, и эта истина заключается в том, что там нет никаких частиц.
Однако опыт Алисы подсказывает ей, что частицы существуют! Но тогда оказывается, что температура, вычисленная Унру, кажется просто фикцией — это не столько свойство плоского пространства как таковое, сколько свойство наблюдателя, испытывающего постоянное ускорение в плоском пространстве.
Однако сама гравитация является такой же «фиктивной» силой в том смысле, что вызываемое ею «ускорение» есть не что иное, как движение по геодезической в искривленной метрике.
Как мы объясняли в главе 2, принцип эквивалентности Эйнштейна гласит, что ускорение и гравитация по сути эквивалентны.
С этой точки зрения нет ничего особенно шокирующего в том, что горизонт черной дыры имеет температуру, равную расчетной Унру температуры ускоряющегося наблюдателя.
Но позвольте нам спросить, какое значение ускорения следует использовать для определения температуры? Отойдя достаточно далеко от черной дыры, мы можем сделать ее гравитационное притяжение настолько слабым, насколько захотим.
Означает ли это, что для определения эффективной температуры черной дыры, которую мы измеряем, нам нужно использовать соответственно малое значение ускорения? Этот вопрос оказывается весьма коварным, поскольку, как мы полагаем, температура объекта не может произвольно уменьшаться.
Предполагается, что оно имеет некоторую фиксированную конечную величину, которую может измерить даже очень далекий наблюдатель.
Теги: #Научно-популярные #Космонавтика #Читальный зал #мозг #книги #книги

-
Рынок Электронных Книг Растёт: Версия Pvi
19 Oct, 24 -
Вопросы Александру Зудину (Paragon Software)
19 Oct, 24 -
Что Вас Раздражает В Gmail?
19 Oct, 24


