При обсуждении предыдущей статьи о проектирование на основе модели Возник резонный вопрос: если использовать экспериментальные данные, можно ли поступить еще проще, занести данные в Системную Идентификацию и получить модель объекта, вообще не заморачиваясь с физикой? Без изучения всяких многоуровневых формул Навье-Стокса, Бернулли и прочих циркулей Штангеля с Рабиновичем? Мы протестировали объект и получили результат. 
Модель ракеты Фау-2 мы представили в виде одной передаточной функции: можно посмотреть здесь.
И вроде все работало.
Зачем нам сначала изучать исчисление и исчисление, когда есть волшебная кнопка, создающая модель из тестов? Действительно, такой подход можно использовать, но для этого необходимы два условия:
- Объект должен уже существовать (не подходит для проектируемых объектов).
- Данные измерений должны быть полными и достоверными.
Например, в эта статья о моделировании электропривода показано, что «при определенном пороговом значении точности средств измерений модель привода становится неидентифицируемой, что приводит к потере управляемости и невозможности диагностики» В этой же статье мы разберем магию и магию создания моделей в виде передаточных функций из ТАУ, а затем проведем сеанс разоблачения этой магии.
Итак, сначала волшебство
Давайте посмотрим на простой пример.У нас есть механическая модель демпфера.
Это поршень на пружине, он движется внутри цилиндра, может двигаться вверх и вниз.
Его положение представляет собой интересующую нас функцию Y(t), сверху на него действует возмущающая сила (U(t)) и на стенки поршня действует сила вязкого трения.
(См.
рисунок 1) 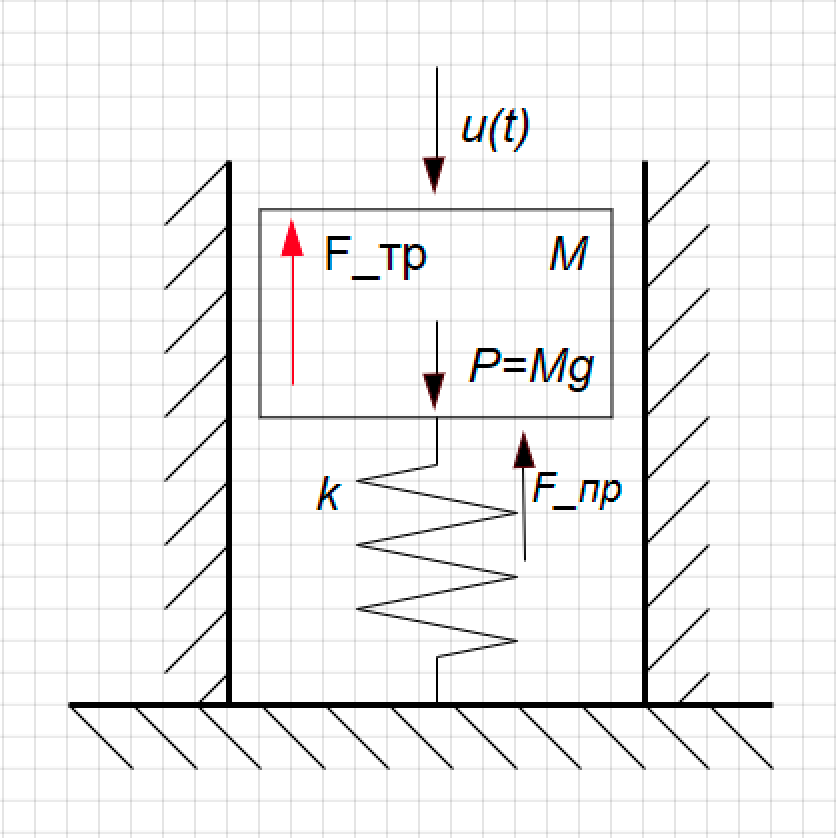
Рисунок 1. Принципиальная схема амортизатора.
Выведем передаточную функцию для этого звена.
Те джедаи, которые уже знакомы с магией передаточных функций, могут пропустить эту часть и сразу перейти к разоблачению магии, а для юных падаванов мы раскроем всю технологию получения динамических уравнений.
Согласно 2-му закону Ньютона ускорение тела пропорционально сумме сил, действующих на тело: 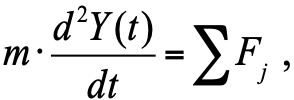
, (1)
Где м - масса тела; Ф дж — силы, действующие на корпус (поршень демпфера).
Подставив в уравнение (1) все силы согласно рис.
1, получим: 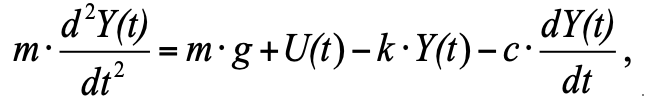
(2)
Где: Y(т) – положение поршня; Р = м∙г - сила тяжести; F_pr = k∙Y(t) – сила сопротивления пружины; 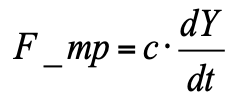
– сила вязкого трения (пропорциональна скорости поршня).
Размеры сил и коэффициентов, входящих в уравнение (2): 
Предположим, что в нулевой момент времени поршень находится в равновесии.
Тогда начальное положение поршня будет y 0 в состоянии равновесия, когда скорость и ускорение равны 0, можно рассчитать по уравнению 2. 
Это уравнение позволяет рассчитать, в каком положении будет находиться поршень при различных нагрузках.
Это статическая характеристика: приложили силу и получили смещение.
Ее вид для нашей системы предельно прост (см.
рис.
2): 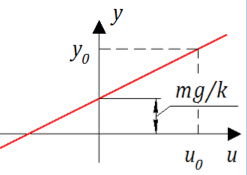
Рисунок 2. Статические характеристики демпфера.
Казалось бы, это счастье – простая линия, приложив силу, получаешь движение.
Но не тут то было! Нас интересует не конечное положение поршня, а процесс перехода из одного состояния в другое.
Для анализа переходного процесса была создана теория автоматического управления ТАУ.
Согласно стандартной «технологии создания моделей», согласно этой теории, предлагается рассматривать систему не в абсолютных величинах, а в отклонениях от равновесного состояния.
Такая формулировка упрощает решение и построение.
И действительно, если заменить абсолютные значения отклонениями, то получим: 
F_pr = k∙(y 0 +y(t)) = k∙y 0 + к∙у(т) – сила сопротивления пружины; 
- сила трения.
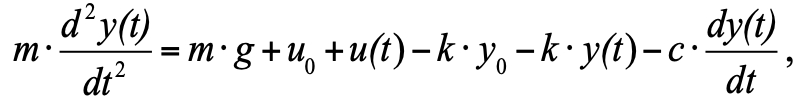
но так как мы приняли, что в начальный момент мы имеем состояние равновесия, а сумма трёх сил в состоянии равновесия равна нулю, то их можно исключить из уравнения, и в результате получим: 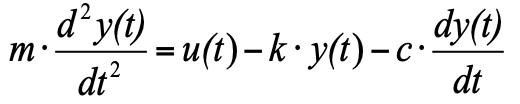
(4)
Чтобы преобразовать уравнение к виду по канону ТАУ, нужно все уравнение разделить на k так, чтобы значение коэффициента y выходной переменной было равно 1, и перенести множители с выходными значениями в правая сторона у(т) , а слева – при входных воздействиях и(т) : 
(5)
Это уравнение уже можно записать в операторной форме: 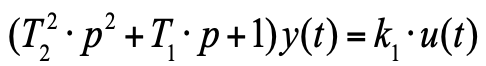
(6)
Где: 
р = д/дт – оператор дифференцирования.
Обратите внимание, что размерности коэффициентов имеют размерность и смысл постоянных времени: 
Передаточная функция для такого уравнения [6] имеет вид: 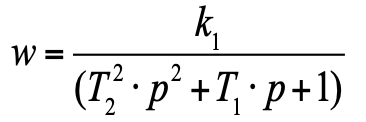
Теперь на ваших глазах мы получили из уравнений физики передаточную функцию в виде блока, причем полученный блок представляет собой стандартное колебательное звено от ТАУ.
Лично для меня магия здесь - это волшебный вид из статических характеристик, частей системы, массы поршня, упругости пружины, трения о стенки) объекта и временной характеристики переходных процессов.
в системе волшебным образом появился
Сверим формулы с моделью
Как он меня научил Максим Андреев , при создании динамических моделей «Конец – это конец всего!» ( смотрите здесь второй принцип моделирования – «начинайте с конца» ): И в конце функции у нас есть движение.Поэтому представим уравнение 2 в форме Коши для перемещения.
Форма Коши – это когда слева стоят производные интересующих нас функций, справа – выражения для их вычисления.
Поскольку производная в уравнении имеет вторую степень, то введя новую переменную Y1 - скорость изменения положения (скорость движения), получим систему двух уравнений в форме Коши: 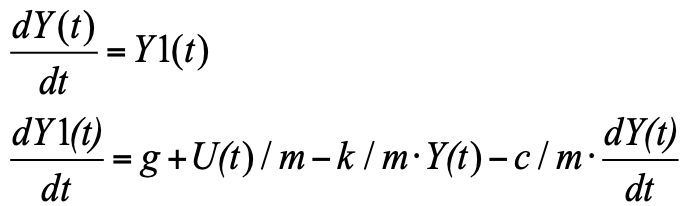
Это уравнение можно просто записать в блоке «Язык программирования» и получить модель (см.
рис.
3): 
Рисунок 3. Модель демпфера на языке программирования.
На входе используем значение силы U, на выходе блока — смещение Y, начальное положение задается по формуле 3. Все переменные задаем как глобальные сигналы для проекта: 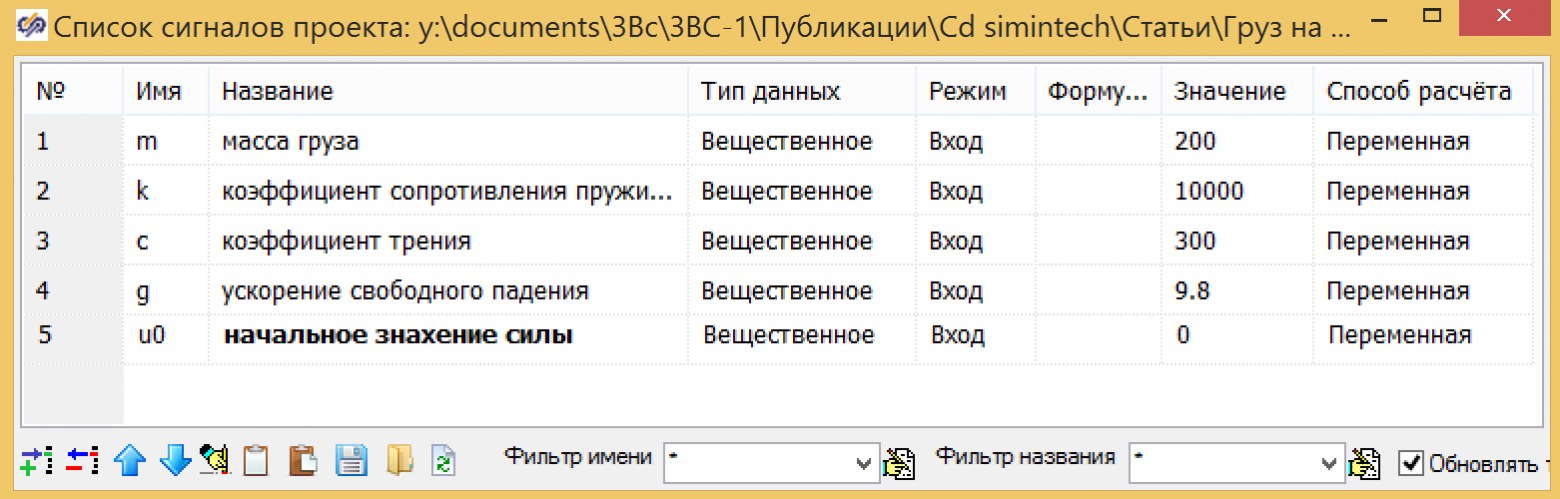
Рисунок 4. Глобальные переменные проекта.
Модель демпфера также может быть создана в виде структуры, на рисунке 5 показана параллельная модель демпфера, созданная из стандартных блоков, в которой начальное условие находится в интеграторе на выходе (см.
рисунок 6), а коэффициенты вводятся в сумматор (см.
рисунок 7) 
Рисунок 5. Демпфер на языке программирования и в виде структурной схемы.

Рис.
6. Свойство интегратора с начальными условиями.
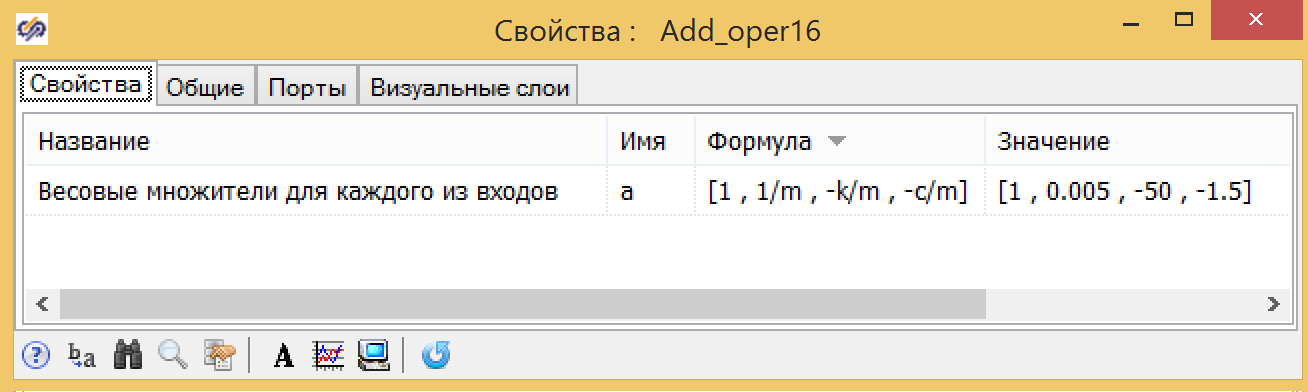
Рисунок 7. Свойства сумматора с коэффициентами.
Зададим возмущающее воздействие на уровне 10 секунд, скачком меняя силу воздействия от 0 до 30, и убедимся, что обе модели показывают одинаковый результат (см.
рис.
8).
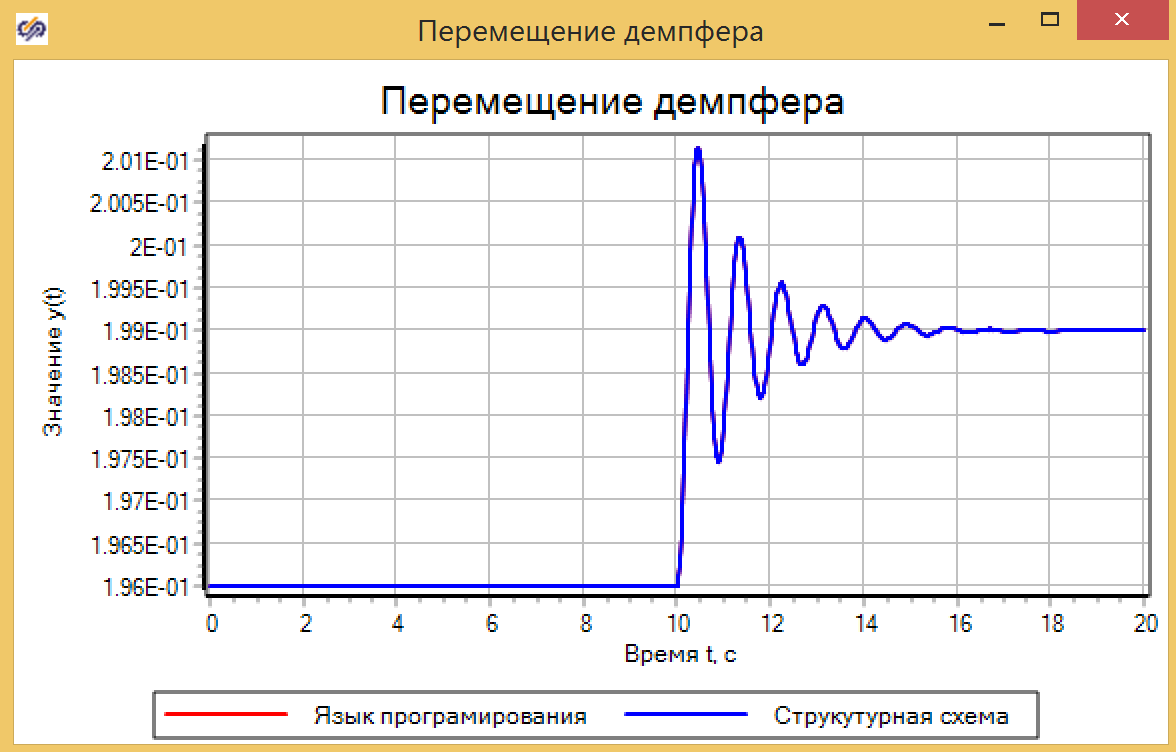
Рисунок 8. Движение демпфера.
Проверим модель в виде передаточной функции в общем виде и в виде колебательного звена, что и представляет собой эта система.
Для этого соберем схему, как показано на рисунке 9. 
Рисунок 9. Две модели демпфера в виде передаточных функций.
Следует учитывать, что диаграмму мы составляли в отклонениях, поэтому для получения абсолютного значения необходимо добавить константу – начальное положение поршня.
Для передаточной функции (формула 7) мы используем те же глобальные константы и выражения, полученные ранее для к 1 , Т 1 , Т 2 (см.
рис.
10).
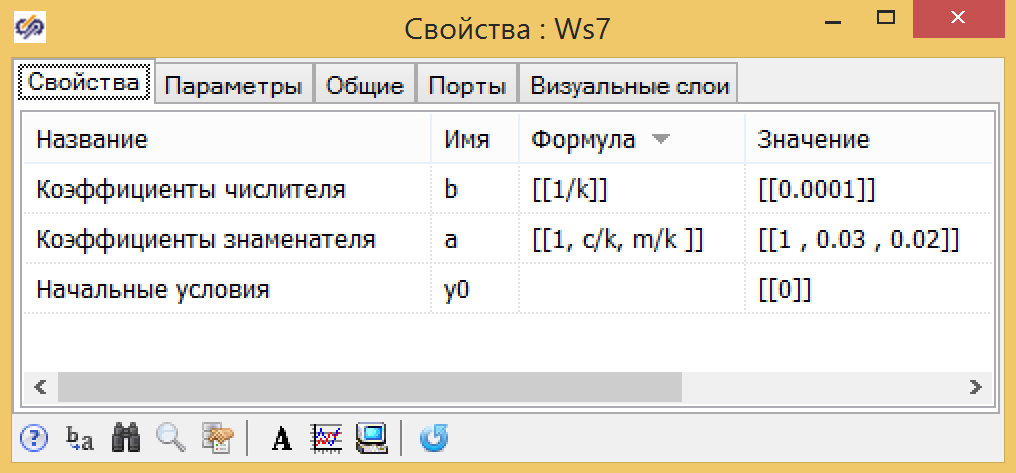
Рисунок 10. Общие параметры передаточной функции.
Для параметров колебательного звена формулы немного сложнее, но все можно выразить и через глобальные параметры: массу поршня - m, коэффициент сопротивления пружины - k, коэффициент трения - с (см.
рис.
11).

Рисунок 11. Параметры колебательного звена.
Графики переходных процессов показывают (см.
рисунок 12), что магия ТАУ действительно работает. Передаточная функция дает точно такие же результаты, как и модель, основанная на уравнениях физики.

Рисунок 12. Движение заслонки в моделях TAU.
Давайте представим, что у нас нет модели, и мы используем блок идентификации на основе данных, полученных в результате эксперимента.
Существует целая технология анализа данных и получения передаточных функций, но в рамках статьи и в качестве примера мы подключим блок построения передаточных функций к модели в виде языка программирования, как показано на рисунке 13. Мы считаем, что наша модель — это «черный ящик», и мы не знаем, что внутри.

Рисунок 13. Схема подключения псевдоидентификатора.
В результате анализа нашего блока на языке программирования мы получили передаточную функцию, практически не отличающуюся от исходной, полученной из уравнений (см.
рис.
14.).
Сравните с рисунком 10. Это волшебная кнопка! 
Рис.
14. Результаты идентификации передаточной функции.
Значения числителя и знаменателя можно напрямую скопировать из блока идентификации, вставить в блок передаточной функции и обеспечить совпадение графиков.
Магия ТАУ работает.
Сеанс магических откровений
Так почему же мы не всегда можем использовать идентификацию системы для процесса модельно-ориентированного проектирования, когда все так волшебно? Чтобы понять недостатки моделей «черного ящика» System Identification, попробуйте ответить на простой вопрос: каков будет прогиб демпфера, если масса поршня увеличится на 30%? Вот тут-то и выясняется, что не все йогурты одинаково полезны.Если у вас есть справедливые уравнения, вы просто меняете массу нагрузки в глобальных переменных расчета и получаете новый переходный процесс и новую передаточную функцию.

В случае, когда вместо честных уравнений физики у вас уже есть готовая передаточная функция, построенная по результатам эксперимента, нужно запустить еще раз и провести эксперимент, чтобы понять, как изменение массы повлияет на поведение модель.
Как говорится, плохая голова ногам покоя не дает. 
Выводы:
- Сидеть и думать об уравнениях физики всегда полезнее и дешевле, чем экспериментировать.
- Модель, полученная из физических уравнений процессов, гораздо вкуснее и полезнее передаточных функций.
- Эксперимент должен уточнить неизвестные коэффициенты или трудноизмеримые параметры.
- Учите физику и будет вам счастье!
Теги: #математика #Алгоритмы #CAD/CAM #matlab #simulink #simulink #scada #передаточная функция #ТАУ #моделирование физических процессов #simintech

-
Как Мы Внедрили Glpi
19 Oct, 24 -
Один Человек, Два Блога: Почему Бы И Нет?
19 Oct, 24 -
Работаем Удаленно. Особенности И Ограничения
19 Oct, 24 -
Ipxe Загружает Установщик Debian Через Http
19 Oct, 24 -
Реализация Механизма Событий В Oracle Bpm
19 Oct, 24 -
Sun Уточнила Планы Выпуска Opensolaris
19 Oct, 24


