Привет, ГТ! Сегодня мы поговорим об одном необычном состоянии света и его не менее необычных применениях.
Добро пожаловать в кот. 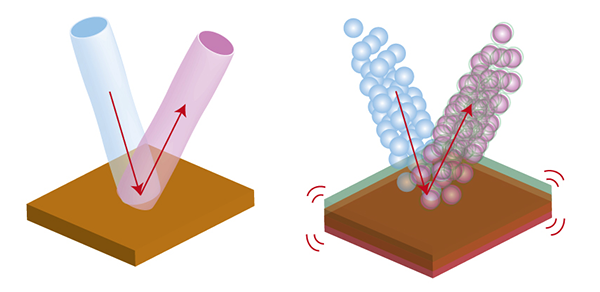
Полицейский останавливает Гейзенберга за превышение скорости.
– Ты хоть знаешь, с какой скоростью ты ехал? - Нет, но я точно знаю, где я был.
(шутка о бороде) Соотношение неопределенности Гейзенберга запрещает одновременное измерение положения и скорости (импульса) частицы.
При этом никто не мешает точно измерить одну из величин – но тогда неопределенность второй станет еще большей.
Вообще, соотношения неопределенностей встречаются в физике довольно часто.
Например, такое же соотношение справедливо и для электромагнитной волны: оно связывает ее амплитуду и фазу: 
Из-за этой неопределенности мы не можем точно измерить синусоиду, описываемую волной; для наблюдателя это всегда будет в шумовой дымке: 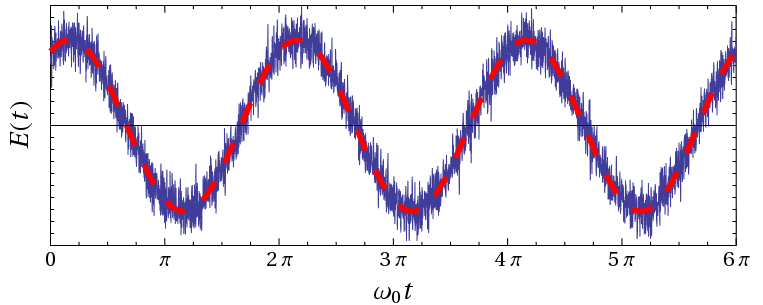
Это можно наглядно показать на круговой диаграмме, где амплитуда соответствует расстоянию от начала координат до точки, а фаза соответствует углу между направлением на точку и осью X. Зеленый цвет показывает неопределенность: 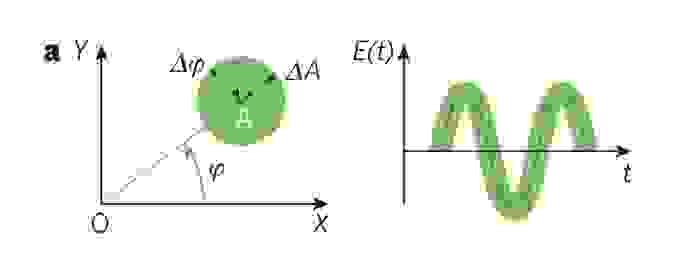
При этом никто не мешает точно определить ни амплитуду, ни фазу.
Тогда круг ошибки превратится в эллипс, сжимающийся в одну сторону и вытягивающийся в другую: 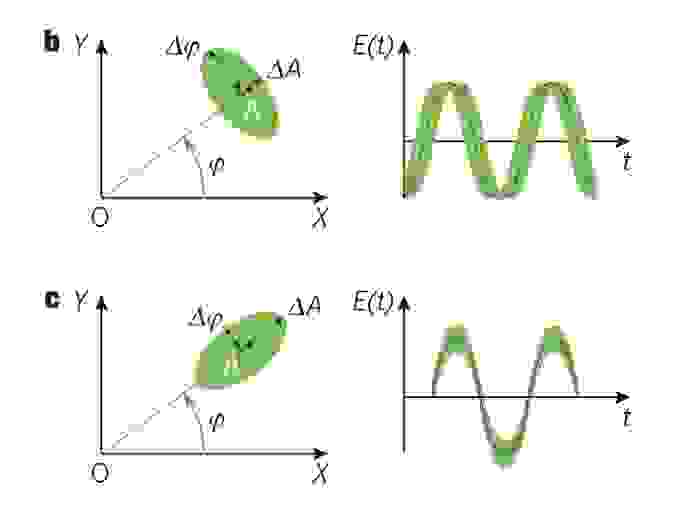
Это состояние называется сжатый свет , поскольку колебания амплитуды или фазы сжимаются вдоль одной из осей, что снижает погрешность измерения.
Первый называется амплитудное сжатие : эллипс вытянут по радиусу, и амплитуду волны можно точно измерить в максимуме и минимуме.
Второй - фаза : эллипс по радиусу, можно измерить фазу волны в нулях синусоиды.
Почему это необходимо?
Для обычного света (например, лазера) мы не можем измерить амплитуду или фазу точнее, чем нам дает круг погрешности.Это называется стандартный уровень квантового шума .
Но сжатый свет позволяет нам «нырнуть» под этот уровень, убрав шум из нашего измерения куда-то еще, где он нас не будет беспокоить.
В каком-то смысле мы можем проводить более точные измерения, чем хотелось бы природе.
Пример
Любой источник света каждую секунду генерирует целое число фотонов.Из-за квантовой природы света он меняется каждую секунду.
Понаблюдав за источником некоторое время, мы можем вычислить распределение числа фотонов.
Слева пример такого распределения для лазера, посередине — для лампочки: 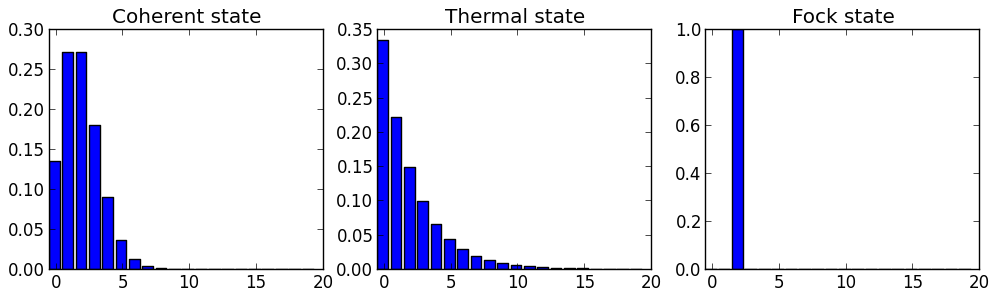
По оси X — количество фотонов, по оси Y — вероятность увидеть такое-то количество фотонов в единицу времени.
Видно, что даже для лазера интенсивность (= количество фотонов) немного «шумит», меняясь от секунды к секунде.
Это стандартный уровень квантового шума.
Но если бы мы могли создать источник, генерирующий одинаковое количество фотонов каждую секунду (рисунок справа), то интенсивность была бы строго постоянной и лишенной какого-либо шума.
Тогда поток фотонов будет строго периодическим: 
Это пример света, максимально сжатого по амплитуде.
Приложения
В отличие от других экзотических объектов, применение сжатого света оказалось очень перспективным.Телеком.
Передача информации путем модуляции сжатой переменной (амплитуда (AM) или фаза (FM), более общий термин для квадратуры) позволяет увеличить отношение сигнал/шум.
Можно построить усилители, добавляющие шум только к той квадратуре, которая несжата и не несет полезного сигнала.
Квантовая запутанность.
В некоторых случаях можно провести параллели между запутыванием фотонов и сжатием света.
Например, можно запутать два луча света: один сжатый по амплитуде, второй сжатый по фазе.
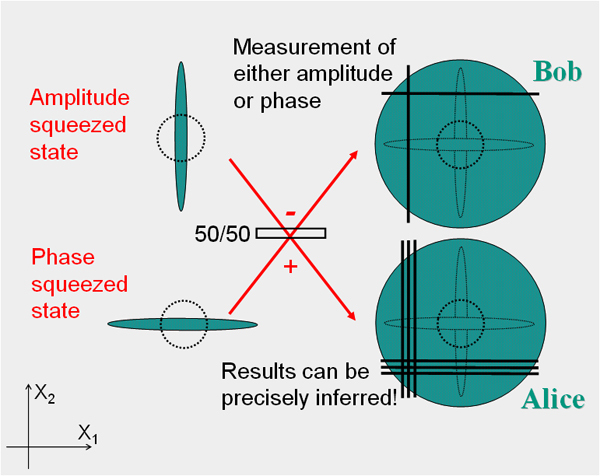
Квантовая криптография.
Это следует из квантовой запутанности и рисунка выше.
В простейшей схеме квантовой криптографии Алиса передает информацию Бобу, используя случайно поляризованные фотоны.
Роль поляризации может сыграть направление сжатия: если оно выбрано неправильно, злоумышленник, перехвативший канал связи, будет измерять не сигнал, а шум.
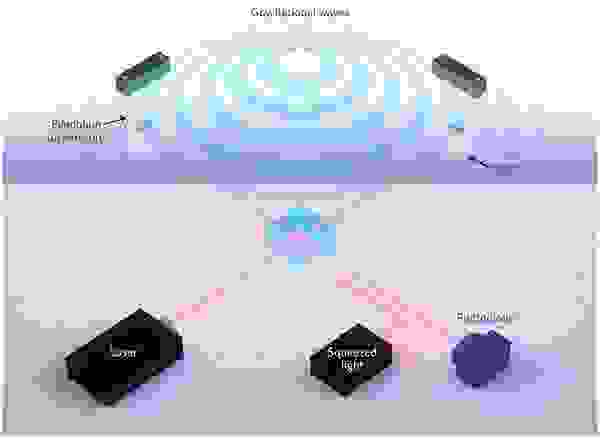
Детекторы гравитационных волн.
Для этой задачи необходимо улавливать мельчайшие вибрации огромных грузов.
Обычно это делается с помощью интерферометра Майкельсона.
Его структура очень проста: лазер, два зеркала и одна полупрозрачная пластина: 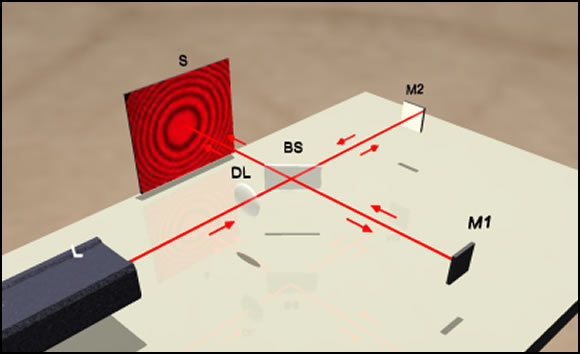
Лазер отражается от двух зеркал, два отражения интерферируют, и на экране формируется интерференционная картина.
Если одно из зеркал двигается, то и картинка тоже движется.
Происходит это из-за изменения фазы волны: зеркало отошло – путь лазера стал немного длиннее, пришла дополнительная фаза – сдвинулись интерференционные полосы.
Поскольку интерферометр измеряет фазу, его разрешение не может быть лучше неопределенности фазы.
Для обычного лазера он ограничен стандартным уровнем квантового шума.
Но если мы заменим лазер источником фазосжатого света, эта проблема исчезнет, и мы сможем измерять расстояния с беспрецедентной точностью.
Сегодня это делается на одном из крупнейших детекторов гравитационных волн GEO600 и, судя по всему, планируется для космического детектора LISA. Кстати, среди пользователей GT есть Шкафф , который занимается именно этим и готов ответить на ваши вопросы в комментариях.
Точное измерение фазы.
Фазово-сжатый свет может быть полезен для измерения фазового контраста — рутинного метода в современной биологии.
Как сгенерировать?
Обычно для этой цели используются нелинейно-оптические процессы.Например, в некоторых кристаллах имеется Керровская нелинейность – зависимость показателя преломления от силы света.
Пошлем на такой кристалл лазерный импульс.
Центр импульса, где амплитуда максимальна, больше всего изменит показатель преломления кристалла и добавит максимальную фазу при прохождении волны через кристалл.
На фронтах импульсов фазовый сдвиг, напротив, будет минимальным.
Это растянет круг неопределенности в эллипс, образуя сжатое состояние:
Как обнаружить?
Вы также можете измерить сжатый свет несколькими способами.1. Схема Хэнбери Брауна–Твисса.
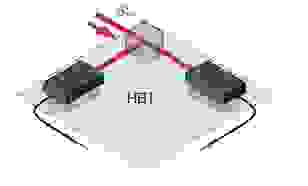
В сериале о Хэнбери Брауне и Твиссе Я же говорил вам, что корреляционная функция g (2) соответствует ширине распределения числа фотонов.
Амплитудное сжатие света означает, что количество фотонов определяется лучше, чем обычно.
Поэтому в широком смысле слова г (2) меньше единицы — признак сжатого света.
2. Балансный детектор.
Это похоже на схему Хэнбери Брауна-Твисса, только вместо корреляций мы либо вычитаем, либо складываем сигналы с двух диодов (по своему усмотрению): 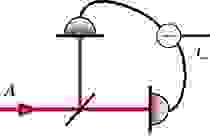
Полупрозрачное зеркало пропускает или отражает каждый фотон случайным образом.
Эта случайность вносит дополнительный квантовый шум (тип выстрела).
Такой шум имеет на двух диодах разный знак: если фотон отразится, то он не пролетит; если оно пролетело, оно не отразится.
Если вычесть сигнал одного диода из другого, то квантовый шум не исчезнет. А что, если мы сложим это? Тогда шум исчезнет, потому что у него другой знак.
(Еще одно объяснение: мы разделили свет на две части, а затем соединили их вместе — дополнительного шума это явно не добавляло.
) Итак, вычитание добавляет нам шума на стандартном квантовом уровне, а сложение ничего не меняет. Если исследуемый свет был сжат по амплитуде (т. е.
«тихий»), то вычитание сделает его более шумным, а сложение оставит неизменным.
Переключаясь между сложением и вычитанием, мы можем измерить уровень шума, а если он другой, то наблюдаем сжатый по амплитуде свет. 
Вот как выглядит шум после сложения (красный) и вычитания (синий).
Красный шум гораздо слабее и соответствует сжатому свету.
3. Гомодинация.
Амплитудное сжатие измерить легко, но что делать с фазовым сжатием? Если вы сможете «повернуть» ориентацию эллипса (то есть фазу света), то свет изменится со сжатого по фазе на сжатое по амплитуде.
Фазу можно вращать, смешивая свет с опорной волной.
Это очень похоже на гетеродинный приемник, только в гетеродине частота опорной и исследуемой волн различна, а в гомодине нет (отсюда и название).
Даже в гомодине нужно подбирать фазу опорной волны.
В электронике это делается фазовращателем, в оптике - линией задержки (чем позже приходит свет, тем больше опережает фазу).
Смешивание происходит на том же полупрозрачном зеркале: 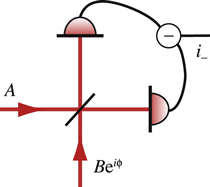
Опорная волна приближается снизу.
А дальше – тот же балансный детектор.
И еще интересная вещь
Пока сжатый свет используется только в сверхточной интерферометрии.Проблема в том, что он оказывается невероятно хрупким.
Это легко понять на примере идеального сжатого по амплитуде света (поток фотонов строго периодический): 
При распространении света неизбежны потери, которые всегда случайны.
Это означает, что фотоны будут исчезать из потока случайным образом: 
Как видите, от периодичности почти ничего не осталось.
Как и от сжатия.
Поэтому сжатый свет очень сложно передать на большие расстояния.
И напоследок полюбуемся схемой гравитационного детектора GEO 600 под Ганновером: 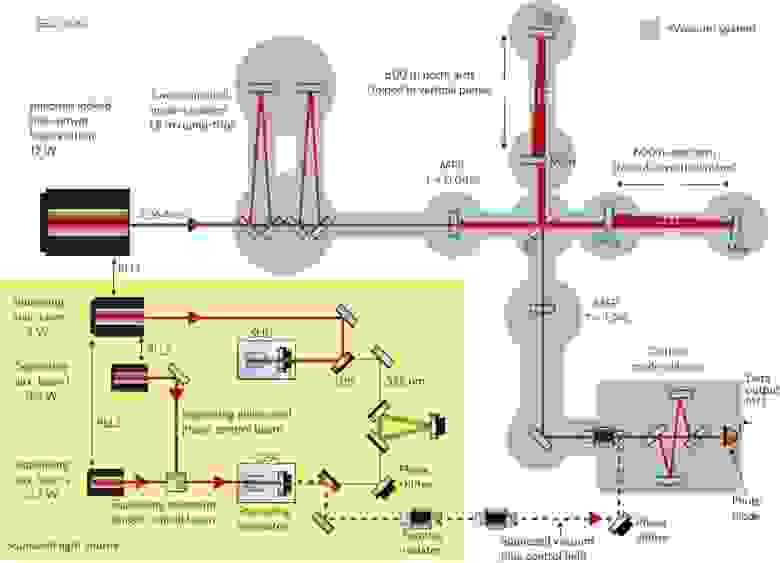
Источник сжатого света находится на желтом фоне.
Он использует нелинейный оптический процесс, но не керровскую нелинейность, а генерацию излучения второй гармоники.
Красная пунктирная линия — сжатый свет. Справа вверху – интерферометр Майкельсона с плечом 600 метров; зеркала подвешены на грузах, которые должны колебаться под действием гравитационных волн.
Изображение с интерферометра получается на фотодиоде в правом нижнем углу.
Источники М.
Фокс.
Квантовая оптика: Введение – Издательство Оксфордского университета, 2006. Спасибо Шкафф за ваши комментарии.
Изображений: КДПВ , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 .
Теги: #Популярная наука #лазеры #физика #квантовая оптика #квантовая оптика #сжатый свет

-
Seo-Оптимизация Сайта Для Нового Блога
19 Oct, 24 -
Ipad — Очередная Революция Apple :)
19 Oct, 24 -
80 Из 20 – Как Не Оптимизировать Процессы
19 Oct, 24 -
Предупреждения Для Фрилансеров
19 Oct, 24 -
Корпоративный Туалет
19 Oct, 24 -
Даже У Функций Есть Предел...
19 Oct, 24


