Введение Эта статья является продолжением серия статей описание алгоритмов, лежащих в основе Синет — фреймворк для запуска предварительно обученных нейронных сетей на ЦП.
В предыдущем статья Я описал методы, основанные на умножении матриц.
Эти методы при минимальных усилиях позволяют достичь во многих случаях более 80% теоретического максимума.
Казалось бы, где можно еще улучшиться? Оказывается, это возможно! Существуют математические методы, позволяющие сократить количество операций, необходимых для свертки.
В этой статье мы рассмотрим один из этих методов — алгоритм свертки с использованием метода Винограда.

Шмуэль Виноград 1936.01.04 - 2019.03.25 — выдающийся израильский и американский учёный-компьютерщик, создатель алгоритмов быстрого умножения матриц, свертки и преобразования Фурье.
Немного математики
Хотя в машинном обучении чаще всего используются свертки с квадратным ядром, для упрощения изложения сначала рассмотрим одномерный случай.
Пусть у нас есть входное одномерное изображение размера
:
и размер фильтра
:
тогда результат свертки будет:
Эти выражения будет удобно переписать в матричной форме:
где используются обозначения:
На первый взгляд последняя замена выглядит несколько бессмысленной — операций явно больше.
Но выражения
И
необходимо рассчитать только один раз.
С учетом этого нам нужно выполнить всего 4 операции умножения, тогда как в исходной формуле их нужно сделать 6.
Перепишем выражение (1) еще раз:
Где
обозначает поэлементное умножение, также используются следующие обозначения:
Выражение (2) можно обобщить на двумерный случай:
Необходимое количество операций умножения для
будет сокращено с
до
.
Таким образом, мы получаем вычислительный выигрыш в
раз.
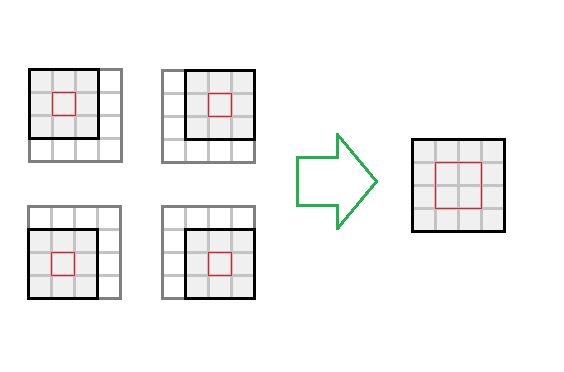
Если визуализировать, то по сути вместо того, чтобы отдельно рассчитывать свертку для каждой точки изображения, мы будем вычислять ее сразу для блока размером
: 
В произвольном случае для свертки с окном
и размер блока
необходимое количество умножений будет
а выигрыш описывается формулой:
В пределе для достаточно больших
И
Для любой свертки достаточно всего 1 операции умножения на точку! К сожалению, увеличение размера блока приводит к быстрому увеличению затрат на преобразование входных данных.
и выходной
изображений, поэтому на практике вы обычно не используете размер блока больше, чем
.
Пример реализации
Для практической реализации алгоритма Винограда хотелось бы рассмотреть простейший случай — свертку с ядром.
для блока
.
Чтобы еще больше упростить изложение, мы также предположим, что во входном изображении нет отступов, а размеры входного и выходного изображений кратны 2. Реализация свертки, основанной на умножении матриц, будет выглядеть так:
Тем, кто хочет подробно разобраться в том, что здесь происходит, следует обратиться к моему предыдущая статья .float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } }
Текущая реализация получается из предыдущей, если положить: strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0.
Модифицированный алгоритм свертки
Позвольте мне еще раз процитировать формулу (6):Если мы перейдем от выходного изображения размера
к изображению произвольного размера, то нам придется разбить его на блоки размера
.
Для каждого такого блока
значения, которые входят в 16 преобразованных
входные изображения уменьшаются вдвое.
Каждая из этих 16 матриц затем умножается на соответствующую матрицу преобразованных весов.
.
Полученные 16 матриц преобразуются в выходное изображение.
.
Схема этого процесса представлена ниже: 
С учетом этих замечаний алгоритм свертки примет вид: void convolution(const float * src, int batch, int srcC, int srcH, int srcW,
int kernelY, int kernelX, int dilationY, int dilationX,
int strideY, int strideX, int padY, int padX, int padH, int padW, int group,
const float * weight, const float * bias, float * dst, int dstC, float * buf)
{
const int block = 2, kernel = 3;
int count = (block + kernel - 1)*(block + kernel - 1); // 16
int dstH = srcH - kernelY + 1;
int dstW = srcW - kernelX + 1;
int tileH = dstH / block;
int tileW = dstW / block;
int sizeW = srcC * dstC;
int sizeS = srcC * tileH * tileW;
int sizeD = dstC * tileH * tileW;
int M = dstC;
int N = tileH * tileW;
int K = srcC;
float * bufW = buf;
float * bufS = bufW + sizeW*count;
float * bufD = bufS + sizeS*count;
set_filter(weight, sizeW, bufW);
for (int b = 0; b < batch; ++b)
{
set_input(src, srcC, srcH, srcW, bufS, sizeS);
for (int i = 0; i < count; ++i)
gemm_nn(M, N, K, 1, bufW + i * sizeW, K,
bufS + i * sizeS, N, 0, bufD + i * sizeD, N));
set_output(bufD, sizeD, dst, dstC, dstH, dstW);
for (int i = 0; i < M; ++i)
for (int j = 0; j < N; ++j)
dst[i*N+ j] = relu(dst[i*N + j] + bias[i]);
src += srcC*srcH*srcW;
dst += dstC*dstH*dstW;
}
}
Количество операций, которые потребуются без учета преобразований входного и выходного изображений: ~srcC*dstC*dstH*dstW*count .
Далее мы опишем алгоритмы преобразования весов, входных и выходных изображений.
Преобразование сверточных весов
Как видно из выражения (6), над весами свертки необходимо выполнить следующее преобразование:, где матрица
определяется в выражении (4).
Код такого преобразования будет выглядеть так: void set_filter(const float * src, int size, float * dst)
{
for (int i = 0; i < size; i += 1, src += 9, dst += 1)
{
dst[0 * size] = src[0];
dst[1 * size] = (src[0] + src[2] + src[1])/2;
dst[2 * size] = (src[0] + src[2] - src[1])/2;
dst[3 * size] = src[2];
dst[4 * size] = (src[0] + src[6] + src[3])/2;
dst[5 * size] = ((src[0] + src[6] + src[3]) +
(src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4;
dst[6 * size] = ((src[0] + src[6] + src[3]) +
(src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4;
dst[7 * size] = (src[2] + src[8] + src[5])/2;
dst[8 * size] = (src[0] + src[6] - src[3])/2;
dst[9 * size] = ((src[0] + src[6] - src[3]) +
(src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4;
dst[10 * size] = ((src[0] + src[6] - src[3]) +
(src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4;
dst[11 * size] = (src[2] + src[8] - src[5])/2;
dst[12 * size] = src[6];
dst[13 * size] = (src[6] + src[8] + src[7])/2;
dst[14 * size] = (src[6] + src[8] - src[7])/2;
dst[15 * size] = src[8];
}
}
К счастью, это преобразование нужно выполнить только один раз.
Поэтому на конечную производительность это не влияет.
Преобразование входного изображения
Как видно из выражения (6), над входным изображением необходимо выполнить следующее преобразование:, где матрица
определяется в выражении (3).
Код такого преобразования будет выглядеть так: void set_input(const float * src, int srcC, int srcH, int srcW,
float * dst, int size)
{
int dstH = srcH - 2;
int dstW = srcW - 2;
for (int c = 0; c < srcC; ++c)
{
for (int row = 0; row < dstH; row += 2)
{
for (int col = 0; col < dstW; col += 2)
{
float tmp[16];
for (int r = 0; r < 4; ++r)
for (int c = c; c < 4; ++c)
tmp[r * 4 + c] = src[(row + r) * srcW + col + c];
dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]);
dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]);
dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]);
dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]);
dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]);
dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]);
dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]);
dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]);
dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]);
dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]);
dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]);
dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]);
dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]);
dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]);
dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]);
dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]);
dst++;
}
}
src += srcW * srcH;
}
}
Количество операций, необходимых для этого преобразования: ~srcH*srcW*srcC*count .
Преобразование выходного изображения
Как видно из выражения (6), над выходным изображением необходимо выполнить следующее преобразование:, где матрица
определяется в выражении (5).
Код такого преобразования будет выглядеть так: void set_output(const float * src, int size,
float * dst, int dstC, int dstH, int dstW)
{
for (int c = 0; c < dstC; ++c)
{
for (int row = 0; row < dstH; row += 2)
{
for (int col = 0; col < dstW; col += 2)
{
float tmp[8];
tmp[0] = src[0 * size] + src[1 * size] + src[2 * size];
tmp[1] = src[1 * size] - src[2 * size] - src[3 * size];
tmp[2] = src[4 * size] + src[5 * size] + src[6 * size];
tmp[3] = src[5 * size] - src[6 * size] - src[7 * size];
tmp[4] = src[8 * size] + src[9 * size] + src[10 * size];
tmp[5] = src[9 * size] - src[10 * size] - src[11 * size];
tmp[6] = src[12 * size] + src[13 * size] + src[14 * size];
tmp[7] = src[13 * size] - src[14 * size] - src[15 * size];
dst[col + 0] = tmp[0] + tmp[2] + tmp[4];
dst[col + 1] = tmp[1] + tmp[3] + tmp[5];
dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6];
dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7];
src++;
}
dst += 2*dstW;
}
}
}
Количество операций, необходимых для этого преобразования: ~dstH*dstW*dstC*количество .
Особенности практической реализации
В рассмотренном выше примере мы дали описание алгоритма Винограда для блока размером.
На практике чаще всего используется более продвинутая версия алгоритма:
.
В этом случае размер блока будет
, а число преобразованных матриц равно 36. Вычислительный выигрыш согласно формуле (8) достигнет 4 .
Общая схема алгоритма та же, различаются только матрицы алгоритмов преобразования.
Есть небольшой проект на Github , что позволяет вычислять эти матрицы с коэффициентами для произвольного размера ядра свертки и размера блока.
Мы представили версию алгоритма Винограда для формата изображения НЧВ , но алгоритм можно реализовать аналогично для формата НХВК (Подробнее об этих форматах изображений я говорил в предыдущая статья .
Несмотря на наличие дополнительных преобразований, основная вычислительная нагрузка в алгоритме Винограда (если, конечно, правильно его использовать) по-прежнему лежит на умножении матриц.
К счастью, это стандартная операция и эффективно реализована во многих библиотеках.
Функции преобразования, оптимизированные для разных платформ для алгоритма Винограда, можно найти Здесь .
Плюсы и минусы алгоритма Винограда
Сначала, конечно, плюсы:- Алгоритм позволяет в несколько раз (обычно в 2-3 раза) ускорить расчет свертки.
Таким образом, можно вычислить свертку быстрее, чем «теоретический» предел.
- В своей реализации алгоритм опирается на стандартный алгоритм умножения матриц.
- Его можно реализовать для разных форматов входных изображений: НЧВ , НХВК .
- Размер буфера для хранения промежуточных значений меньше, чем требуется для алгоритма, основанного на умножении матриц.
- Алгоритм требует отдельной реализации функций преобразования для каждого размера ядра свертки, а также для каждого размера блока.
Может это одна из основных причин того, что почти везде реализовано только для свертки с ядром
. - По мере увеличения размера блока сложность реализации функций преобразования быстро возрастает. Поэтому практически не существует реализаций с размером блока больше
. - Алгоритм накладывает строгие ограничения на параметры свертки.
шагY = шагY = расширениеY = расширениеX = группа = 1 .
Хотя теоретически реализовать алгоритм при нарушении этих ограничений можно, на практике он малопригоден из-за низкой эффективности.
- Эффективность алгоритма снижается, если количество входных или выходных каналов в изображении мало (это связано с затратами на преобразование входных и выходных изображений).
- Эффективность алгоритма снижается при малых размерах входных изображений (полученные матрицы из входного изображения слишком малы по размеру, и стандартный алгоритм умножения матриц становится для них неэффективным).
выводы
Метод расчета свертки, основанный на алгоритме Винограда, позволяет существенно повысить эффективность вычислений по сравнению с методом, основанным на простом умножении матриц.К сожалению, он не универсален и достаточно сложен в реализации.
Для ряда частных случаев существуют более быстрые подходы, описание которых хотелось бы отложить до следующих статей этой статьи.
ряд .
Жду отзывов и комментариев читателей.
Надеюсь, вам было интересно! P.S. Этот и другие подходы были реализованы мной в Структура свертки в библиотеке Симд .
Эта основа лежит в основе Синет — фреймворк для запуска предварительно обученных нейронных сетей на ЦП.
Теги: #Машинное обучение #Алгоритмы #C++ #Обработка изображений #simd #сверточный слой #Метод Винограда

-
Dotnext 2019 Питер: Краткий Отчет
19 Oct, 24 -
Реактивные Веб-Технологии Переоценены
19 Oct, 24 -
Правовые Аспекты Скачивания Музыки И Фильмов
19 Oct, 24 -
Предложение: Пузомерка По «Избранному»
19 Oct, 24


