Добрый день! При просмотре боевиков (фильмов с хорошо проработанными динамическими сценами) иногда в голову закрадывается: а неужели это реально? Например, могла ли машина перевернуться на небольшой скорости, как быстро можно перемахнуть на веревке без начальной скорости над пропастью.

Что на это говорит физика? Интересно написать на бумажке, а потом хвастаться бумажкой с формулами и парочкой векторов? Давайте сделаем это безопасно и четко.
Начнем с обычного математический маятник :
Кстати, даже если в качестве аргумента принять синус, эксперименты с измерением периода маятника дают хорошие результаты для g. Но чтобы любоваться большими углами, нам нужно честно решить уравнение, особенно если scipy предоставляет такую возможность.
Разделим уравнение на два уравнения первого порядка и запишем его в стандартной форме
И теперь мы можем смело кормить этим нашу змею (подробнее о scipy.integrate.odeint увы, в оригинале).
На первом курсе в лаборатории механики были маятники; возможности каждого из них были практически исчерпаны рабочим заданием.t = linspace(0,15,100) G = 9.8 L = 1.0 def diffeq(state, t): th, w = state return [w, -G/L*sin(th)] dt = 0.05 t = np.arange(0.0, 20, dt) th1 = 179.0 w1 = 0.0 state = np.radians([th1, w1]) y = odeint(diffeq, state, t)
Но с одним было что-то не так, потому что это было невозможно сделать, привлекло больше всего внимания маятник Обербека : «Что произойдет, если вы не закрепите гириЭ» И вот, спустя N лет, я увидел в фильме (очередные Пираты Карибского моря), что будет! Хмммм, это действительно правда? Для этого достаточно написать всего два уравнения, первое из которых записано в системе покоя направляющей лопатки с учетом переноса и ускорения Кориолиса.
Куда делась масса гильотины? Как и в большинстве задач без трения, оно было и справа, и слева от равенства, и ни на что не влияет.
Наслаждаемся результатами: 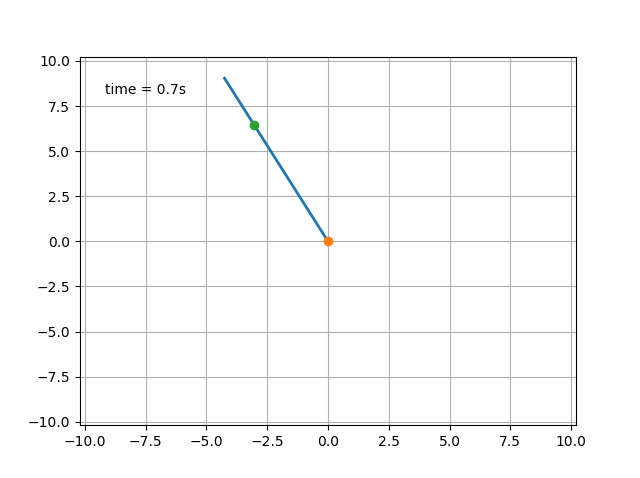
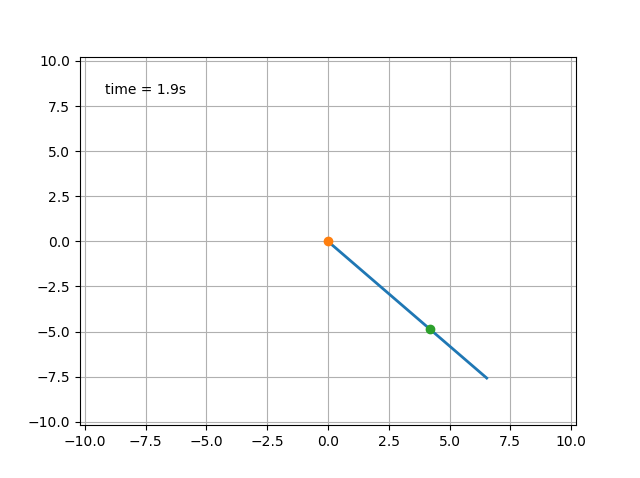
Если начальная скорость велика, то этот «аттракцион» безопасен после прохождения горизонтального положения.
import matplotlib.animation as animation
from pylab import *
from scipy.integrate import *
import matplotlib.pyplot as plt
t = linspace(0,15,100)
G = 9.8
L = 10.0
def derivs(state, t):
th, w, r, v = state
if 0.<r<L or w**2*r>G*cos(th):
return [w, -G/r*sin(th), -v, (-w**2*r-G*cos(th)-G*sin(th)-2*w*v)]
elif w**2*r<G*cos(th):
return [w,-G/r*sin(th),-v, w**2*r-G*cos(th)]
return [w,-G/r*sin(th), 0,0]
dt = 0.01
t = np.arange(0.0, 20, dt)
th1 = 180.0
w1 = 50.
r1 = L*0.9
v1 = 0.0
state = np.radians([th1, w1])
state = np.append(state, [r1, v1])
y = odeint(derivs, state, t)
x1 = L*sin(y[:, 0])
y1 = -L*cos(y[:, 0])
x2 = (y[:,2].
clip(min = 0, max = L))*sin(y[:, 0]) y2 = -(y[:,2].
clip(min = 0, max = L))*cos(y[:, 0]) fig = plt.figure() ax = fig.add_subplot(111, autoscale_on=False, xlim=(-L-0.2, L+0.2), ylim=(-L-0.2, L+0.2)) ax.grid() line, = ax.plot([], [], '-', lw=2) point, = ax.plot(0,0,'o', lw=2) extra, = ax.plot(x1/L*r1,y1/L*r1,'o', lw=2) time_template = 'time = %.
1fs'
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
def init():
line.set_data([], [])
point.set_data(0,0)
time_text.set_text('')
extra.set_data(x1/L*r1,y1/L*r1)
return line, time_text, point, extra
def animate(i):
thisx = [0, x1[i]]
thisy = [0, y1[i]]
thisx2 = x2[i]
thisy2 = y2[i]
point.set_data(thisx[0],thisy[0])
line.set_data(thisx, thisy)
time_text.set_text(time_template % (i*dt))
extra.set_data([thisx2,thisy2])
return line, time_text, point, extra
ani = animation.FuncAnimation(fig, animate, np.arange(1, len(y)),
interval=25, blit=True, init_func=init, repeat = False)
show()
P.S. Здесь начал копать.
P.S.S. Играя с начальными параметрами (при малых углах отклонения от вертикали или малых начальных угловых скоростях), можно прийти к «плоскому» пониманию устойчивости гироскопов.
Лучше нам быть добрыми и не попасть под гильотину! Теги: #физика движения #моделирование #кинематика твердого тела #дифференциальные уравнения #маятник Обербека #python #программирование #математика

-
Грехи Интернета: Мышеловки (И Еще Хуже))
19 Oct, 24 -
Лили, Уильям
19 Oct, 24 -
«Только 5-7% Пк-Геймеров Платят За Игры»
19 Oct, 24 -
Оптимизация Хвостовой Рекурсии В Javascript
19 Oct, 24 -
Как Поднять Боевой Дух Команды Удаленно?
19 Oct, 24 -
Модели Управления: План Или Наглость?
19 Oct, 24


