Создание Симулятора Солнечной Системы

Предисловие Вечная тяга к чему-то новому побудила меня изучить такой замечательный язык программирования, как Python. Как это часто бывает, отсутствие идеи, на реализацию которой было бы не жалко потратить время, сильно замедлило процесс.

Волею судьбы мне попалась замечательная серия статей о создании платформера на Python. здесь И здесь .

Я решил взяться за старый проект. Для симулятора движения тел под действием силы тяжести.

Читайте дальше, чтобы узнать, что из этого получилось.

Первая часть.

Теоретический Чтобы решить проблему, нужно сначала ясно ее представить.

Предположим, всеми правдами и неправдами нам удалось получить двухмерный участок безвоздушного пространства с расположенными в нем телами.

Все тела движутся под действием сил гравитации.

Никакого внешнего влияния нет. Необходимо построить процесс их движения относительно друг друга.

Простота реализации и красочность конечного результата послужат стимулом и наградой.

Освоение Python станет хорошей инвестицией в будущее.

Введем систему координат. Пусть наша система состоит из двух тел: 1. массивная звезда с массой M и центром (x0, y0) 2. легкая планета массы m, с центром в точке (x, y), скоростью v = (vx, vy) и ускорением a = (ax, ay).

Когда нам удастся проанализировать этот случай, мы легко сможем перейти к сложным системам с взаимным влиянием звезд и планет друг на друга.

Сейчас мы поговорим о самых простых вещах.

После несложных манипуляций со вторым законом Ньютона, законом всемирного тяготения и подобными треугольниками я обнаружил, что: топор = G * M * (x0-x) / r^3 ай = G * M * (y0-y) / r^3 Это позволяет создать алгоритм перемещения планеты в гравитационном поле звезды: 1. Перед запуском задайте начальное положение планеты (x, y) и начальную скорость (vx, vy) 2. На каждом шаге вычисляем новое ускорение по формуле выше, после чего пересчитываем скорость и координаты: vx := vx + T * ax vy := vy + T * топор х := х + Т * vx y := y + T * yx Осталось разобраться с константами G и T. Положим G = 1. Для нашей задачи это не столь важно.

Параметр Т влияет на точность и скорость вычислений.

Давайте также поставим 1 для начала.

Часть вторая.

Практичный Итак, моя первая программа на Python. В то же время я хотел бы еще раз поблагодарить вас Велесе для практического руководства.

   

 import pygame, math
 from pygame import *
 from math import *
 
 WIN_WIDTH = 800
 WIN_HEIGHT = 640
 PLANET_WIDTH = 20
 PLANET_HEIGHT = 20
 DISPLAY = (WIN_WIDTH, WIN_HEIGHT)
 SPACE_COLOR = "#000022"
 SUN_COLOR = "yellow"
 PLANET_COLOR = "blue"
 
 #Sun position
 X0 = WIN_WIDTH // 2
 Y0 = WIN_HEIGHT // 2
 #Sun mass
 M0 = 5000
 #Stop conditions
 CRASH_DIST = 10
 OUT_DIST = 1000
 
 def main():
     #PyGame init
     pygame.init()
     screen = pygame.display.set_mode(DISPLAY)
     pygame.display.set_caption("Solar Mechanics v0.1")
     
     #Space init
     bg = Surface((WIN_WIDTH,WIN_HEIGHT))
     bg.fill(Color(SPACE_COLOR))     
     draw.circle (bg, Color(SUN_COLOR), (X0, Y0), 10)
                     
     #Timer init                     
     timer = pygame.time.Clock()
     
     #Planet init
     planet = Surface((PLANET_WIDTH, PLANET_HEIGHT))
     planet.fill(Color(SPACE_COLOR))
     draw.circle (planet,
         Color(PLANET_COLOR),
         (PLANET_WIDTH // 2, PLANET_HEIGHT // 2),
         5)
 
     #Planet to Sun distance
     r = 0.0
     #Initial planet pos, speed and accel
     x = 100.0
     y = 290.0
     vx = 0.1
     vy = 1.5
     ax = 0.0
     ay = 0.0
 
     done = False
     while not done:
         timer.tick(50)
         for e in pygame.event.get():
             if e.type == QUIT:
                 done = True
                 break        
 
         r = sqrt((x - X0)**2 + (y - Y0)**2)
         
         ax = M0 * (X0 - x) / r**3
         ay = M0 * (Y0 - y) / r**3
 
         #New spped based on accel
         vx += ax
         vy += ay
 
         #New pos based on speed
         x += vx
         y += vy
 
         screen.blit(bg, (0, 0))      
         screen.blit(planet, (int(x), int(y)))
         pygame.display.update()     
 
         if r < CRASH_DIST:
             done = True
             print("Crashed")
             break
         if r > OUT_DIST:
             done = True
             print("Out of system")
             break
 
     #Farewell
     print (":-)")
 
 if __name__ == "__main__":
     main()

Вот как выглядит наша система после некоторого моделирования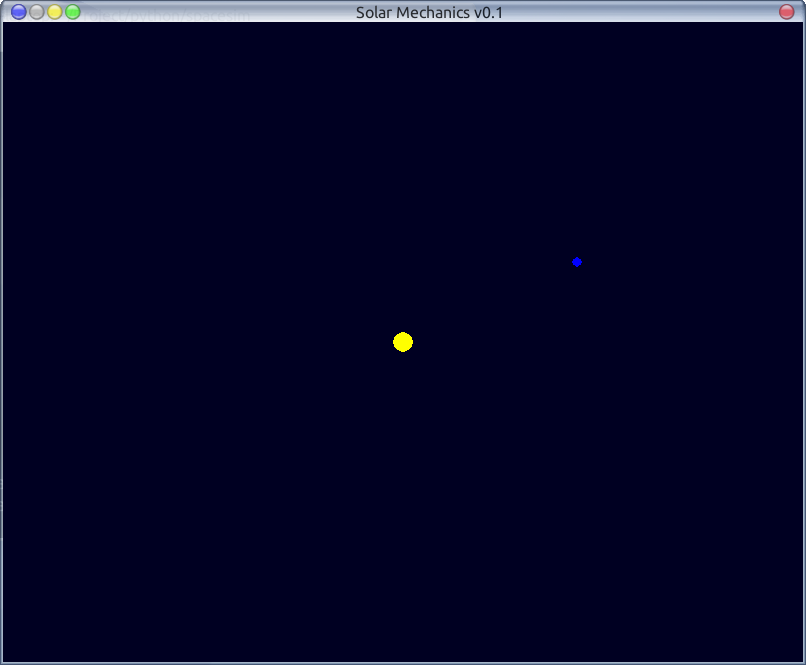

Пока писалась эта заметка, симулятор расширился новым функционалом: количество объектов в звездной системе не ограничено, учитывается их взаимное влияние друг на друга, расчетная часть вынесена в отдельный класс, Конфигурация системы указана в отдельном файле, добавлена возможность выбора систем.
Теперь ищу интересные системные сценарии и небольшие улучшения интерфейса.
Вот пример того, что сейчас находится в разработке: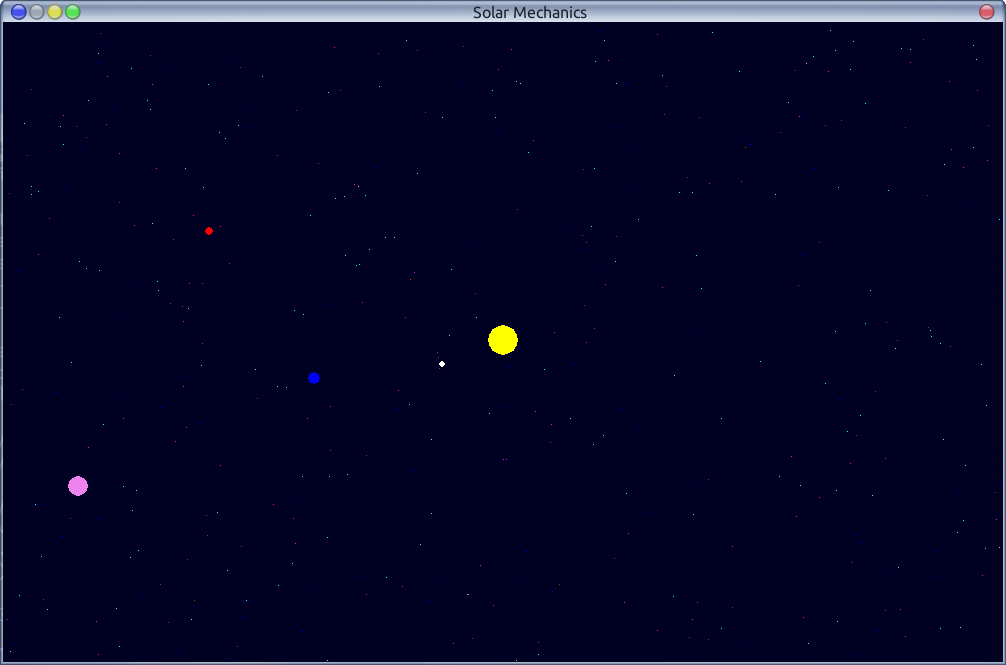

Если эта заметка получит положительные отзывы, обещаю продолжить рассказ о более новой версии.
Обновлять: 1. Я благодарен всем комментаторам за критические замечания.
Они дают много пищи для размышления.
2. Проект вырос.
Все тела уже независимы, влияя друг на друга в соответствии с законом всемирного тяготения.
Рассчитывается N^2 взаимодействий.
Появилась возможность хранить конфигурации звездной системы во внешних файлах и выбирать их при запуске.
Код здесь Запустите так: python3.3 main.py -f .
ini Различные конфигурации - есть.
3. Благодаря комментариям нам удалось найти и устранить главный недостаток - метод расчета координат. В настоящее время используется метод Рунге-Кутты.
Читая «Нежесткие задачи», я буду изучать новые методы.

Теги: #симуляция #руководство #python #разработка игр