Обычно кластеризация предполагает выявление нескольких групп объектов со схожими характеристиками внутри группы и разными характеристиками между группами.
Особенностью совместной кластеризации является группировка не только объектов, но и характеристик самих этих объектов.
То есть если данные представлены в виде матрицы, то кластеризация — это перестановка строк или столбцов матрицы, а совместная кластеризация — это перестановка как строк, так и столбцов матрицы данных.
Как и в моих предыдущих публикациях, примеры использования методов и визуализации решений показаны с использованием данных результатов опросов.
Типичными областями применения алгоритмов совместной кластеризации являются биоинформатика, сегментация изображений и анализ текста.

Для совместной кластеризации данных, как и в случае с кластеризацией, существует множество алгоритмов.
Википедия отчеты не менее 22 методов совместной кластеризации.
В этой статье будут продемонстрированы возможности только одного из них.
Этот метод называется кластеризацией блоков.
Его суть лучше всего выражает картинка, взятая из статьи авторов этого подхода [1].
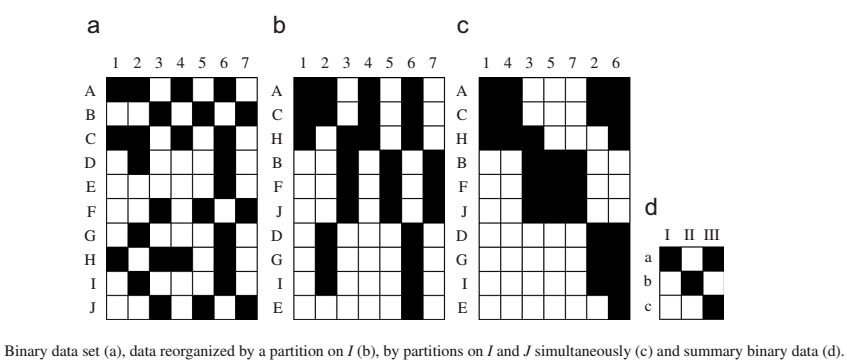
Другими словами, задача состоит в том, чтобы из мозаики данных собрать блочную картинку.
Математически этот метод можно формализовать с помощью процедуры трифакторизации неотрицательных матриц.
Позволять В входная матрица размера п х м .
Его необходимо представить в виде 
Каждая строка матриц р И С содержит ровно одну единицу, остальные элементы — нули.
Единичный элемент ( я Дж ) матрицы р указывает на то, что линия я матрицы В принадлежит дж -й горизонтальный кластер.
Единичный элемент ( к л ) матрицы С указывает, что столбец к матрицы В принадлежит л -й вертикальный кластер.
Матрицы р И С выбираются таким образом, чтобы минимизировать функцию потерь: 
В этом случае Д определяется по норме Фробениуса 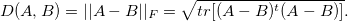
Эта формализация восходит к работе [2], в которой была предложена ортогональная трехфакторизация неотрицательных матриц.
Такая постановка задачи позволяет использовать итерационные методы поиска заданного разложения входной матрицы, аналогичные методам факторизации неотрицательных матриц.
Но в этой публикации будут рассмотрены примеры кластеризации блоков, полученные методом максимального правдоподобия.
Подробности алгоритма можно найти в [1].
Этот подход обычно требует больших вычислительных затрат для поиска решения.
Но есть и преимущества.
Во-первых, с помощью этого метода можно автоматически определить оптимальное с алгоритмической точки зрения количество горизонтальных и вертикальных кластеров для категориальных данных [3].
Во-вторых, алгоритм позволяет учитывать тип входных данных – категориальный (в частности, двоичный) или непрерывный (при этом не требуется, чтобы входные данные были неотрицательными).
Для расчетов будет использоваться пакет Blockcluster [4] среды R. 
Основная цель этой публикации — продемонстрировать возможности визуализации решения для кластеризации.
Отличительной особенностью блочной кластеризации, помимо сегментации данных в обоих направлениях, является то, что при этом типе кластеризации значения входных данных не преобразуются.
Переставляются только строки и столбцы входной матрицы.
Это позволяет визуализировать результат кластеризации «как есть», который легко интерпретировать.
Оговорюсь, что если количество столбцов в матрице измеряется сотнями или тысячами, то, вероятно, потребуется предварительная обработка результата.
Но в задачах анализа результатов опросов, о которых пойдет речь ниже, кластеризация по очень большому числу переменных обычно не требуется.
Что делать, если ваша задача не требует групп переменных, но вы хотите получить представление о блочном представлении ваших данных? Совместная кластеризация не обязательно требует группировки переменных.
Мы начнем именно с такого примера.
Пример 1: Свобода в мире (данные Freedom House, 2015 г.
) Данные Freedom in the World (FIW) представляют собой сравнительную оценку политических прав и гражданских свобод в 195 странах на основе экспертных опросов, проведенных Freedom House. Доступны данные за 2015 год, агрегированные по 7 подкатегориям.
Здесь .
По результатам этих 7 переменных каждой из 195 стран присваивается два рейтинга – политические права и гражданские свободы, а по результатам итоговый статус страны – свободная, частично свободная и несвободная (всего 3 группы).
из этих рейтингов.
Код R с (4,1) совместной кластеризацией данных FIW
Теги: #совместная кластеризация #неотрицательная трифакторизация mtrx #блочная кластеризация #блочные карты #европейский социальный опрос #свобода в мире данных #Интеллектуальный анализ данных #r #Открытые данные #Визуализация данныхlibrary(data.table) library(blockcluster) fiw.2015 <- fread("FIW 2015.csv") fiw.2015.clusters <- cocluster(as.matrix(fiw.2015[,LETTERS[1:7],with=FALSE]), datatype = "categorical",model = "pik_rhol_multi", nbcocluster = c(4,1),

-
Eclipse + Qt: Установка И Настройка
19 Oct, 24


