Троичные вычисления Я готовлю курс лекций по компьютерной архитектуре для студентов нашего университета и в качестве небольшой практической разминки хочу предложить студентам построить примитивный программируемый компьютер на троичной логике.
Конкретно в этой статье рассказывается о базовом модуле, который будет использоваться при построении, а именно о троичном мультиплексоре.
В этом тексте я не буду выходить за рамки простейшего сумматора (и его аппаратной реализации), текст и так достаточно насыщенный.
В последующих статьях я потихоньку расскажу, куда меня приведет эта кривая, так как я в самом начале приключений.
- Сосчитай до трех: один
- Сосчитайте до трёх: два (память)
- Сосчитайте до трех: три (счетчики)
- Счёт до трёх: четыре (одно банально компьютер и три банально командная система)
здесь .
На любые вопросы типа «почему?!» Я заранее отвечаю: «Потому что могу».

Строительный материал: троичный мультиплексор.
Логический уровень
Основным строительным материалом является троичный мультиплексор.
Логически речь идет о пяти выводах: на один из них (sel) подается троичный сигнал селектора, и в зависимости от него на выход мультиплексора (out) подается один из трех входных сигналов inN, inO или inP.
На схемах обычно рисуют примерно так: 
Аналогичным образом работает демультиплексор: в зависимости от селектора один вход подключается к одному из трех выходов.
Аппаратное обеспечение, которое я использую, имеет двунаправленные ключи, поэтому оно является и мультиплексором, и демультиплексором (однако возможности демультиплексирования я пока не использую).
Аппаратная реализация
Аппаратный дизайн принадлежит Александр Шабаршин , я это честно говоря просвистел целиком.Единственное, что я сделал, так это установил аппаратуру для поверхностного монтажа, потому что.
Эти микросхемы существенно дешевле выходных микросхем; в Китае их можно приобрести по 50 центов за штуку.
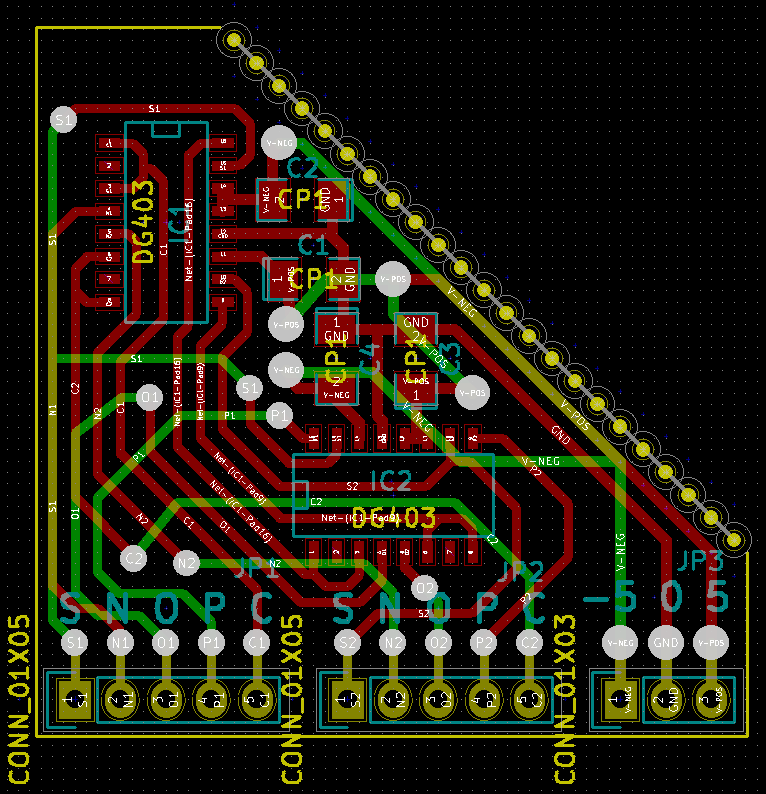
До того, как я наткнулся на эту конструкцию (кстати, по троичным вычислениям и аппаратному обеспечению для них есть много информации на Александра форум ), я пробовал городить огород с помощью cd4016 и cd4007, что получалось, но было крайне громоздко и неудобно.
Использование ключей dg403 дает настоящий троичный элемент без какой-либо избыточности, например кодирование троичной системы в двухбитную двоичную систему.
Между прочим, в отличие от многих теоретиков, Александр пошел гораздо дальше; разработал и заказал собственные микросхемы, работающие на троичной логике: 
Для создания одного мультиплексора TRIMUX Александр использовал две микросхемы переключателя dg403, одну с питанием логики между -5В и 0В, а вторую между 0В и 5В, что позволяет работать с троичным сигналом, представленным тремя уровнями напряжения -5, 0 и 5В.
Но при этом половина ножек остаётся свободной, поэтому два троичных мультиплексора как раз помещаются в два чипа dg403. 
Как это использовать? Функции с одним аргументом
Опустим тривиальную тождественную функцию, которую можно получить, применив -1, 0, 1 к соответствующим входам мультиплексора.
Во-первых, давайте добавим единицу ко входному сигналу A (конечно, в кольце -1,0,1): 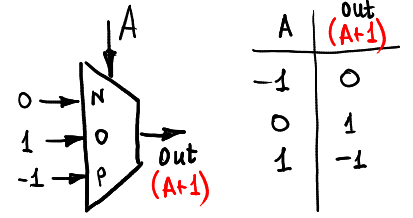
И вот как мы можем вычесть одно:
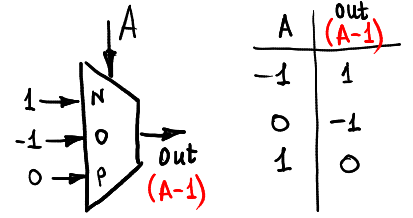
Вот как мы можем вычислить функцию одного аргумента max(A,0):

И вот так min(A,0):
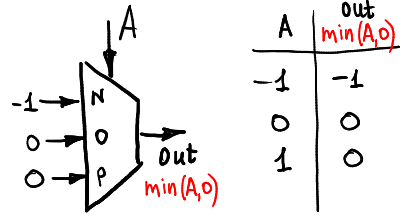
Две функции аргумента: полусумматор
А+Б
Итак, одного мультиплексора нам достаточно для вычисления функции одного аргумента.Для расчета функции двух аргументов придется использовать три или четыре мультиплексора.
Например, если мы хотим вычислить сумму двух троичных сигналов A и B (все еще внутри кольца -1,0,1), то мы можем использовать следующую схему: 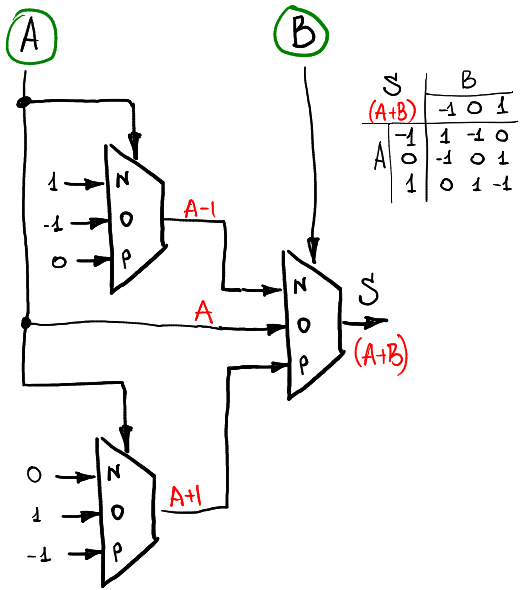
Первый уровень мультиплексоров учитывает функции одного аргумента от сигнала А, а второй использует их в зависимости от уровня сигнала Б.
Консенсус
Если мы хотим вычислить функцию консенсуса по двум троичным сигналам (она равна -1, если A=B=-1, и равна 1, если A=B=1, в противном случае равна нулю), то это можно сделать так:
Аппаратная реализация
Итак, мы только что создали полусумматор .
В зависимости от двух входов A и B он производит два выхода S и C, которые можно рассчитать как A+B = S + 3*C.
Давайте проверим это! Красный диод = -1, выключен = 0, зеленый = 1. Таким образом, это фото говорит нам, что S=-1, C=1, то есть 1+1 = -1 + 3*1: 
На этой табличке даны все девять возможных состояний нашего полусумматора, каждая ячейка дает соответствующие значения S и C. По ссылкам в ячейках вы найдете соответствующие фотографии железа.
| С, С | Б | |||
| -1 | 0 | 1 | ||
| А | -1 | 1,-1 | -1,0 | 0,0 |
| 0 | -1,0 | 0,0 | 1,0 | |
| 1 | 0,0 | 1,0 | -1,1 |
Три функции аргумента: полный сумматор
Полный сумматор должен принимать на вход три аргумента, а не два, как полусумматор.Третий аргумент — перенос из младшего порядка.
Итак, по трем входам A,B и Cin нам нужно вычислить два выхода S и Cout по закону A+B+Cin = S + 3*Cout.
Сумма трех тритов
Для функции трёх аргументов идея точно такая же, как и для функции двух: мы используем послойную подготовку данных для последующих вычислений.
То есть первый уровень мультиплексоров принимает на вход только A, второй — только B, а последний мультиплексор — только Cin.
Вот как может выглядеть схема расчета S: 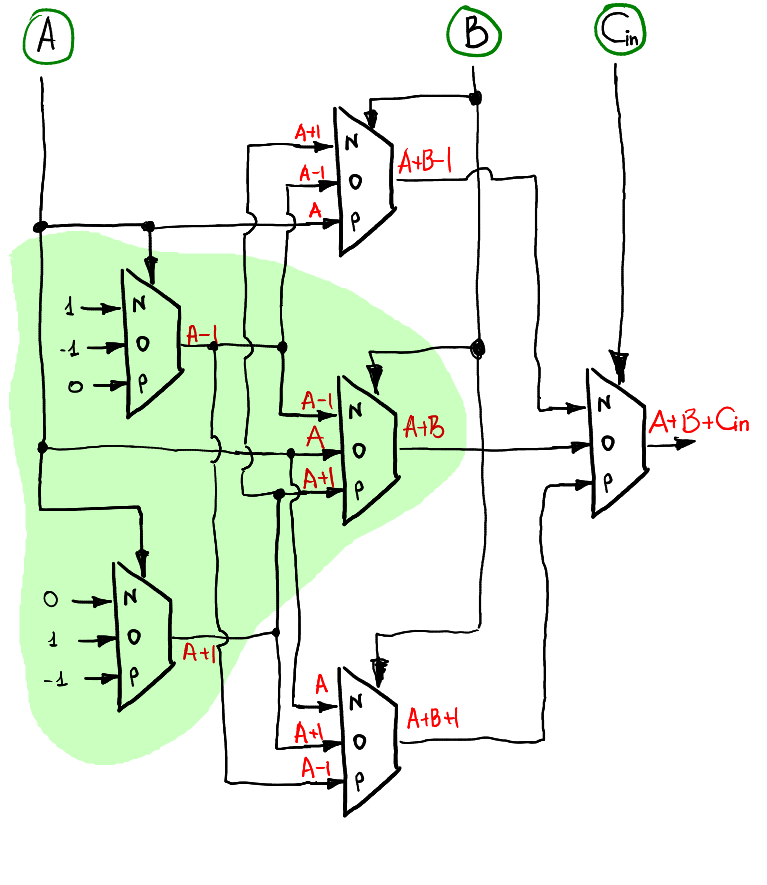
Обратите внимание, что при Cin = 0 это должно фактически повторять работу полусумматора.
Логично, что полусумматор включен в схему полного сумматора (выделен зеленым).
Переполнение результата
Точно так же рассчитывается трит переполнения, и точно так же в схему входит схема расчета трита переполнения полусумматора:
Аппаратная реализация
В этот раз мне было лень тыкать провода в макетную плату, поэтому я быстро подключил плату:
И сдул многовековую пыль с запасов гетинакас:

Вот все 27 возможных состояний полного сумматора.
Обратите внимание, что средняя таблица (которая предназначена для Син=0 ) повторяет таблицу для полусумматора.
| Син = -1 | Б | |||
| -1 | 0 | 1 | ||
| А | -1 | 0,-1 | 1,-1 | -1,0 |
| 0 | 1,-1 | -1,0 | 0,0 | |
| 1 | -1,0 | 0,0 | 1,0 |
| Син = 0 | Б | |||
| -1 | 0 | 1 | ||
| А | -1 | 1,-1 | -1,0 | 0,0 |
| 0 | -1,0 | 0,0 | 1,0 | |
| 1 | 0,0 | 1,0 | -1,1 |
| Син = 1 | Б | |||
| -1 | 0 | 1 | ||
| А | -1 | -1,0 | 0,0 | 1,0 |
| 0 | 0,0 | 1,0 | -1,1 | |
| 1 | 1,0 | -1,1 | 0,1 |
Вот так выглядит бутерброд для двух категорий: 
Вот как он решает пример -4 + 2 (левая доска — младшая цифра): 
На самом деле, конечно, для младшей цифры нам не нужен полный сумматор; полусумматора будет вполне достаточно, поскольку нам не нужно передавать на вход сумматора младшую цифру.
Но полусумматор я уже разобрал на макетной плате, а собирать обратно лень :)
Заключение
В этой статье я кратко описал, что и как можно построить базу для троичных вычислений.В будущих выпусках ожидайте счетчиков, памяти, ALU и т. д. Следите за обновлениями! Теги: #троичный калькулятор #пальцевые вычисления #Аномальное программирование #Занимательные задачи #Алгоритмы #математика #Программирование на микроконтроллерах

-
Проекты Разработки Dynamics Ax На X++
19 Oct, 24 -
Удаленное Управление Hyper-V Из Winxp
19 Oct, 24 -
Nagios: Уведомление По Sms
19 Oct, 24 -
Фильтры Матричной Обработки Изображений
19 Oct, 24 -
Основные Ошибки Веб-Издателей
19 Oct, 24


