Сегодня я опишу еще несколько свойств прогнозирования временных рядов.
А именно цикличность и усложнение варианта со схожими сегментами.

Вернемся к графику из предыдущая статья .
Этот график очень периодический (см.
рисунок ниже), и правильно было бы сначала спрогнозировать его, рассчитав цикличность.
Используя только расчет цикличности, я получил прогноз ошибки 4,1% (mape) вместо 5% для предыдущей экспериментальной точки.
После расчета цикличности мы вычитаем из начальных значений графика прогнозные значения из цикличности и пытаемся предсказать полученный график ошибок с помощью корреляций.
В результате по этому же пункту я уже получил ошибку 3,7%.
Программа и ее исходники текущей версии Здесь .
Теперь он больше похож на отдельную утилиту для серийного прогнозирования, а не на тестирование одного метода и одного графика.
И может выполнить прогноз для последней точки, для которой нет фактического прогнозируемого значения.
А теперь подробнее об алгоритмах и значениях
обезьяна — Абсолютная процентная ошибка — абс(прогноз-факт)/факт карта — Средняя абсолютная процентная ошибка Если мы возьмем несколько обезьян за период и вычислим среднее арифметическое, то получим мапе.Сам по себе процент ошибки прогноза для неизвестного расписания мало о чем говорит. Потому что неизвестно, насколько обычно меняется расписание, и соответственно, много оно было предсказано или мало.
Для сравнения удобно взять карту из прогноза, который составлен в предположении, что следующее значение будет таким же, как и последнее известное.
Для экспериментальной точки это значение составляет 9,2%.
Напомню, что цифры там были даны как прогноз на день вперед. Те.
колебания графика за день составляют 9,2%.
В результате использования прогнозирования эта ошибка сократилась до 3,7%.
Вот как выглядит исследуемый график за несколько дней с сильными дневными колебаниями: 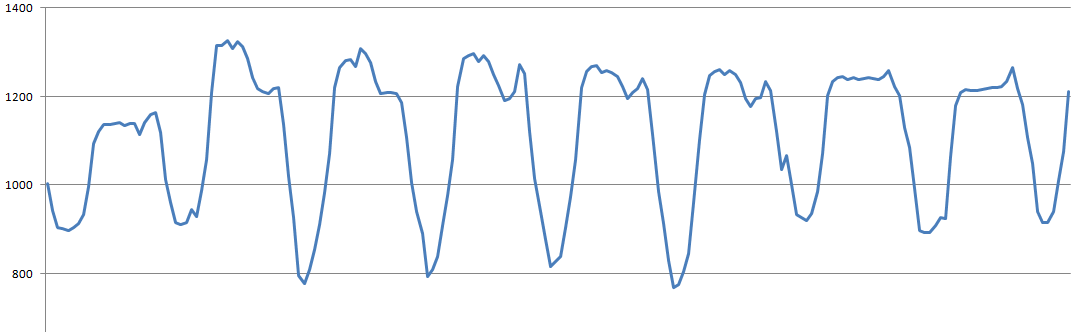
Очевидно, что если такой график замучать корреляциями, то в корреляции будут наблюдаться преимущественно суточные колебания, а все более мелкие нюансы будут заглушены.
Вот как выглядит прогноз на предстоящий день: 
Фактический график показан красным, прогноз - синим, предел трех стандартных отклонений прогноза от центра - зеленым - если бы колебания графика имели стандартное распространение , то это будет 99% вероятного коридора графика.
Расчет цикличности
Для выполнения прогнозов на основе цикличности было организовано занятие Езда на велосипеде в файлах езда на велосипеде.ч
И циклинг.cpp
.Объект этого класса накапливает N средних элементов, количество которых соответствует длине цикла.
Средние накапливаются по регулируемой формуле, они называются скользящими средними.
В моей интерпретации эта формула имеет корректировочную длину, что удобнее, чем просто безликий коэффициент. Этот механизм относится к компактному классу Средняя адаптация в файле дисперсия.
ч И дисперсия.
cpp .
В среднем суть механизма заключается в следующем:
В этом классе есть еще одна сложность с отрицательной интерпретацией cnt_adapt, если интересно, посмотрите исходный код. В общем, на уроке Езда на велосипеде Имеется N элементов регулируемых средних, среди них есть текущий элемент, к которому добавляется очередное значение, и указатель перемещается на следующий элемент средних.cnt_vals = cnt_vals + 1; if (cnt_vals > cnt_adapt) su = su - su / (double)cnt_adapt + new_value; else su = su + new_value; mean = su / (double)min(cnt_vals, cnt_adapt);
При достижении последнего элемента указатель перемещается в начало.
И так по кругу.
Точнее это делалось просто на уроке ar_means[cnt_values % size_cicling] , где cnt_values — количество добавленных значений.
Прежде чем добавить новое значение к текущему среднему элементу, текущее среднее значение вычитается из нового значения, тем самым генерируя значение ошибки.
Сорт Езда на велосипеде может рекурсивно содержать следующий уровень цикличности Велоспорт* ne_level , если да, то ошибка текущего уровня передается для суммирования следующей цикличности, в противном случае возвращается ошибка.
Для текущего графика основная цикличность дневная – 24 часа и недельная – 168 часов.
Это создает разницу между переданным фактическим значением и текущим значением циклических средних значений.
Если применить к этому механизму ноль в обратном направлении и добавить к нему все средние значения текущего шага, но только без модификации элементов Средняя адаптация , то мы получаем значение прогноза, исходя из предположения, что будущая ошибка равна нулю.
Смещаем текущий элемент средних на следующий, по-прежнему без изменений, и снова в обратном порядке подаем ноль.
Результатом является график прогноза, основанный на суммировании всех средних значений.
Для этого механизма остается два вопроса: как определить периодичность возможных цикличностей и как определить наилучшую длину адаптации.
Я сделал это, просто просматривая тестовые данные.
В программе имеется кнопка сканирования цикличности, которая сканирует все возможные циклические периоды размером до двух тысяч и отображает лучший из них.
Этот лучший вручную добавляется в поле «Периоды цикличности» и при следующем запуске поиска цикличности он будет сканироваться за вычетом новой добавленной цикличности.
Только если вы посмотрите на текущий график, то лучшие цикличности уже внесены в поле по умолчанию и больше их не будет. Так что сотрите их и запустите.
Длина адаптации также подбирается перебором, но указывать ее нигде не нужно; программа сканирует его заново каждый раз при запуске, потому что это ненадолго.
Последовательность указания периодов в поле «Периоды цикличности» также не важна, поскольку при запуске будет выбрана лучшая последовательность.
Кажется, что все циклично.
Они вычисляются, вычитаются из графика, и мы получаем график ошибок.
Мой вариант реализации сходства сегментов
Этот график ошибок представляет колебания со средним значением, близким к нулю, плюс и минус ошибки.Он может содержать корреляции или может быть оставшейся случайной составляющей.
Теперь мы можем применить к нему корреляцию сегментов.
И по этому вопросу скажу, что рассчитывать его с помощью корреляции Пирсона – не лучший вариант. Для этого есть и логические аргументы - такое соотношение создает подобие графики разной интенсивности, хотя при разных интенсивностях последующее поведение вовсе не означает, что оно будет одинаковым, только с переносом.
А практические показания заключаются в том, что после применения цикличности попытка применить корреляцию Пирсона только ухудшает результат. А также при использовании без цикличности прогноз хуже, чем при цикличности.
В результате экспериментов я пришел к выводу, что лучший расчет сходства — это просто квадратичная разница между графиками.
Если у графа уже минус цикличность, то граф болтается около нуля, и достаточно просто квадратичной разницы между ними.
Если цикличность не вычиталась, то лучше использовать квадратичную разность, но с предварительным вычитанием среднего: 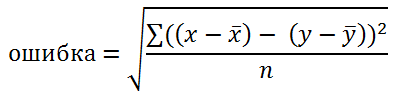
Хоть я и пишу здесь, что это соотношение отрезков, на самом деле я имею в виду квадратичную разность между ними.
В демонстрационной программе вы можете выбрать различные параметры сходства/корреляции, которые я тестировал, и проверить их на других нужных вам графиках.
Реализация расчета сходства в программе осуществляется классом КоррСлайд в файлах corr_slide.h И corr_slide.spp .
Формулы различного сходства рассчитываются в методе CorrSlide::Res CorrSlide::get_res(.
) .
Помимо различных вариантов расчета, упомянутых выше, в этот класс входит оптимизация, благодаря чему вам не придется пересчитывать расчет для соседних сегментов свойств, описанных ниже.
Что я сделал, так это то, что для каждой позиции было просканировано множество различных длин корреляции.
Берется первая длина, скажем 6 пунктов, следующий вариант длины в два раза длиннее, т.е.
12, затем следующие 24 и т.д. Для каждой длины накапливается пачка лучших похожих отрезков и средний прогноз и дисперсия.
рассчитываются.
После чего из всех посчитанных пакетов, каждый из которых отвечает за разную длину, выбирается тот, который лучше всего предсказывает текущую точку.
Тот, который имеет наименьшее отклонение прогноза, является лучшим.
Ошибочно полагать, что самый длинный отрезок будет лучшим.
Во-первых, для длинного отрезка может не оказаться достаточного количества совершенно одинаковых отрезков или их вообще не будет. И брать лучший по своему подобию, как я уже говорил в предыдущей статье, было бы неправильно.
Во-вторых, прогноз может коррелировать от значительно более близких значений к прогнозируемой точке, и последующее удлинение отрезка не даст лучшего ответа, а лишь разбавит пакет лучших ненужными отрезками.
Но самый короткий отрезок, как вы понимаете, не будет лучшим.
В результате просто собираются несколько пачек коррелирующих отрезков разной длины и смотрят, какая из пачек имеет наиболее определенный прогноз – наименьшую дисперсию.
Также я сделал вариант расчета сходства с увеличением значимости значений ближе к прогнозируемой точке.
Там при каждом увеличении длины в два раза дважды добавляется тот отрезок, который был в два раза короче.
Вот как это выглядит. Вот как это выглядит, указанные ниже суммы являются составляющими корреляционных формул: void CorrSlide::make_res_2() {
for (int i_len = 0; i_len < c_lens-1; ++i_len) {
Calc& calc = ar_calc_2[i_len];
if (i_len == 0)
calc = ar_calc[i_len];
else
calc = ar_calc_2[i_len-1];
Calc& calc_plus = ar_calc[i_len+1];
calc.cnt += calc_plus.cnt;
calc.su_s += calc_plus.su_s;
calc.su_s_pow2 += calc_plus.su_s_pow2;
calc.su_m += calc_plus.su_m;
calc.su_m_pow2 += calc_plus.su_m_pow2;
calc.su_s_m += calc_plus.su_s_m;
calc.div_s = dbl(calc.cnt) * calc.su_s_pow2 - calc.su_s * calc.su_s;
}
}
И немного о выбросах
Плюс я еще сделал механизм устранения выбросов.В принципе, выбросы следует считать элементами графика или вероятными ошибками.
Но их необходимо учитывать на уровне формирования распределений, характерных для текущего графика.
Сейчас я основывал расчеты в основном на принципах, которые корректно работают на стандартных дистрибутивах.
Поэтому текущая версия просто указывает, сколько экстремумов следует исключить.
Оно указывается в поле «Количество выбросов» и применяется в нескольких точках расчета, что заметно исказило результат. Проблема с распределениями влияет и на коэффициент прогнозирования, о котором я писал в предыдущей статье; не ясно.
Анализ этих вопросов я оставил для следующей версии программы.
Что произошло в конце
В итоге всё это многообразие и безобразие приводит к тому, что после вычитания цикличности этот график можно предсказать даже чуть лучше.Если вы попробуете разную длину таких отрезков, успех прогноза может несколько измениться.
Те.
результат не стабилен.
Если использовать сходство по квадратическому отклонению, то это в принципе всегда улучшает результат после цикличности обработки, в отличие от корреляции Пирсона.
Также несколько лучшие результаты получаются при использовании длин сходства отрезков, кратных 24 — минимальная цикличность.
Расчет осуществляется достаточно быстро, что можно указать, чтобы учитывалась тысяча и более позиций, и посмотреть средний прогноз за этот период, убедившись, что прогноз успешен не только в экспериментальной точке.
Хотя не везде это так очевидно.
Например, для периода в 1000 позиций, где каждый шаг прогнозируется на 1 шаг вперед, результат будет: средняя ошибка за выбранный период 1,76473% средняя ошибка только по цикличности 1,78332% средняя ошибка при условии, что прогноз представляет собой последнюю известную позицию 4,19216% Если поле «Количество прогнозируемых позиций» оставить пустым, то расчет будет производиться для каждой позиции, начиная с «Даты начала прогноза/позиции» и до конца графика.
Если интересно посмотреть цифры, которые я дал относительно экспериментальной точки, то в настройках по умолчанию нужно изменить «Количество позиций прогноза» = 1, «Количество одной позиции» = 24. Стоит отметить, что все эти улучшения не позволили нам ни на грамм сдвинуть прогноз EURUSD. Кажется, что он совершенно независим от своей прошлой истории.
Хотя я еще проверю это со следующими версиями программы.
Как я уже говорил, программа универсальна, в ней вы можете выбрать свои файлы данных, указать столбец прогноза и столбец даты, если таковой имеется.
Разделителем столбцов может быть запятая или точка с запятой.
Программа по возможности содержит описания элементов управления.
На этом пока все, в следующий раз улучшу результат прогнозирования новыми свойствами.
Теги: #математика #прогнозирование

-
Как Красиво Разрезать Торт
19 Oct, 24 -
Уязвимость Локального Корня Linux 3.8
19 Oct, 24 -
Гипервзгляд На Riw 2009
19 Oct, 24 -
Исправление Alt-Tab В Labview
19 Oct, 24



