Привет, Хабр! Представляю вашему вниманию перевод статей из блога ZCash, в которых описан механизм работы системы доказательства с нулевым разглашением SNARKs, используемой в криптовалюте ZCash (и не только).
Источник: https://z.cash/blog/snark-explain5.html Предыдущие статьи: Часть 1: СНАРК объяснил.
Гомоморфное сокрытие и слепая полиномиальная оценка (перевод) Часть 2: СНАРК объяснил.
Знание принятых коэффициентов и надежный слепой расчет полиномов (перевод)
Введение от переводчика
Начиная заключительную часть перевода, хочу сказать, что мы живем в поистине удивительные времена.Время, когда высшая математика имеет возможность практически сразу участвовать в разработке программного обеспечения и мы можем наблюдать «в действии» результаты работы математиков технологических институтов над передовыми вещами на основе блокчейнов и обмена данными.
Что ж, не буду больше задерживать ваше внимание, перейдем к самому интересному.
От вычислений к полиномам
В предыдущих статьях мы разработали конкретный механизм работы с полиномами.В этой части мы научимся преобразовывать утверждения, которые хотим доказать и проверить, в полиномиальный язык.
Идея использования полиномов таким образом начинается с новаторская работа в 1991 году Лунд, Фортноу, Карлофф и Нисан (Карстен Лунд, Лэнс Фортноу, Ховард Карлофф - Чикагский университет И Ноам Нисан - Еврейский университет).
Еще один выйдет в 2013 году.
еще одна прорывная работа Дженнаро, Джентри, Парно и Райкова (Розарио Дженнаро, Крейг Джентри, Брайан Парно, Мариана Райкова).
Эта работа определила чрезвычайно удобное преобразование вычислений в полиномы, названное программой квадратичной арифметики (QAP).
KAP стали основой современных разработок zk-SNARK, в частности тех, которые используются в криптовалюте ZCash. В первой части статьи преобразование расчетов в КАП будет объяснено на примере.
Даже если вы сосредоточитесь на небольшом примере, а не на общем определении, вам придется потратить немало времени на его понимание с самого начала.
Так что будьте готовы к некоторым умственным усилиям :)
Предположим, Алиса хочет доказать Бобу, что она знает.
такой, что
.
Первым шагом является представление расчета с
в виде арифметической схемы.
Арифметические схемы
Арифметическая схема состоит из вычисляемых арифметических операций, называемых ветвями, таких как сложение и умножение, со связями между ними.
В нашем случае схема выглядит так: 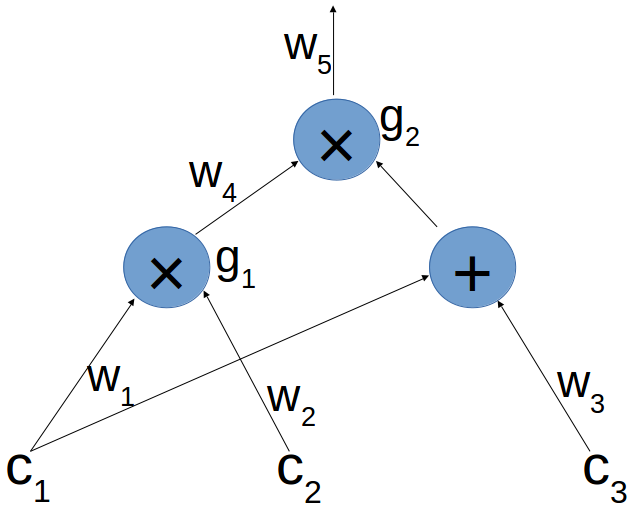
Соединения внизу — это входы, а верхнее выходное соединение — результат расчета всей схемы для данных входов.
Как видно на рисунке, разъемы и переходы схемы обозначены определенным образом.
Эти правила понадобятся для следующего шага, а именно передачи схемы в КАП:
- Когда один и тот же исходящий соединитель входит в более чем один переход, он считается одним и тем же соединителем - например.
в примере. - Предполагается, что блоки умножения имеют ровно два входа, которые называются левым и правым разъемами.
- Соединители, идущие от сложения к умножению или сложению, не отмечены.
Считается, что входные параметры переходов сложения поступают непосредственно в переход умножения.
В примере предполагается, что
И
являются входами
Итак, для нашей схемы допустимый набор назначений:
Где
И
Следуя этой терминологии, Алиса хочет доказать, что она знает допустимый набор присваиваний.
такой, что
.
Следующий шаг — преобразовать это утверждение в полином с помощью CAP.
Доведение до КАП
Каждый переход умножения должен быть связан с элементом поля:будет коррелировать с
И
С
.
Давайте назовем точки {1, 2} наш целевые точки .
Теперь нам нужно определить набор «левых соединяющих полиномов».
, «правые соединительные полиномы»
и «выходные соединительные полиномы»
.
Основная идея этого действия заключается в том, чтобы значения полиномов были равны нулю во всех целевых точках, кроме целевой точки перехода умножения, в котором они участвуют.
Говоря конкретно, потому что
соответственно левый, правый и выходной разъемы
, можно определить
, поскольку полином
равен единице в точке 1 соответствующий
и равен нулю в точке 2 соответствующий
.
Заметь
И
оба являются правильными входами
.
Поэтому аналогично определяем
, потому что
равен единице в целевой точке 2 соответствующий
и ноль в другой целевой точке.
Обозначим все остальные многочлены как нулевые многочлены.
Для фиксированных значений
они используются в качестве коэффициентов для определения левого, правого и выходного полинома «суммы».
То есть мы можем определить:
Затем мы определяем многочлен
Теперь, после всех этих определений, мы можем сформировать центральное определение:
является допустимым набором назначений схемы тогда и только тогда, когда П принимает нулевое значение во всех целевых точках.
Давайте посмотрим это на нашем примере.
Предположим, что мы определили
как указано выше, с некоторыми
.
Давайте оценим все эти полиномы в целевой точке.
1 :
Из всех
только
отлично от нуля в точке 1 .
Так,
.
Аналогично мы получаем
И
.
Следовательно,
.
Вы можете получить аналогичный
.
Другими словами, п исчезает в целевых точках тогда и только тогда, когда
является допустимым набором назначений.
Теперь воспользуемся следующим алгебраическим фактом: для многочлена п и точки
, у нас есть
тогда и только тогда, когда полином
делит п без остатка, т.е.
для некоторого полинома ЧАС .
Определив целевой полином следующим образом:
, мы поняли это Т делит п тогда и только тогда, когда
является допустимым набором назначений.
На основании вышеизложенного мы определяем КАП следующим образом:
Программа квадратичной арифметики вопрос заказ д и размер м состоит из многочленов
и целевой полином Т заказ д .
Набор заданий
удовлетворяет вопрос если, определяя
И
, существует Т , которое делится без остатка п .
Следуя этой терминологии, Алиса хочет доказать, что она знает набор заданий.
, удовлетворяющий KAP, определенному выше, где
,
Подведем итог этой части.
Мы видели, как утверждения типа «Я знаю
такой, что
«можно перевести в эквивалентное утверждение о полиномах с использованием CAP. Далее мы рассмотрим эффективный протокол для проверки знаний о допустимом наборе назначений CAP.
Выше мы постарались привести достаточно краткий пример доведения до КАП.Мы также рекомендуем отличный пост Виталику Бутерину дополнительную информацию по конвертации программы в КАП.
Протокол Пиноккио
Ранее мы показали, что утверждение, которое Алиса хочет доказать Бобу, можно преобразовать в эквивалентную форму на «полиномиальном языке», называемом программой квадратичной арифметики (QAP).В этой части мы покажем, как Алиса может отправить Бобу достаточно короткое доказательство того, что у нее есть действительный набор назначений для CAP. Мы будем использовать Протокол Пиноккио , разработанный Брайаном Парно, Джоном Хауэллом, Крейгом Джентри, Марианой Райковой.
Как указано выше, Алиса хочет доказать, что у нее есть действительный набор назначений, который имеет некоторые дополнительные ограничения, например.
.
Но мы не будем здесь это учитывать и для простоты покажем, как легко доказать знание некоторого допустимого набора заданий.
Если у Алисы есть допустимый набор присваиваний, это означает, что если мы определим
как описано выше, то существует некий полином ЧАС такой, что
.
В частности, для любого
у нас есть
.
Теперь предположим, что у Алисы нет допустимого набора назначений, но она также определяет
из какого-то недопустимого набора
.
Тогда вы можете быть уверены, что Т не делит п .
Это означает, что для любого многочлена ЧАС нет высшего порядка д , п И
будут разные многочлены.
Заметь п И
здесь у них порядок не выше
.
Чтобы доказать это, мы будем использовать знаменитая лемма Шварца-Зиппеля, который утверждает, что два разных многочлена степени не выше
могут пересекаться не более чем
точки
.
Таким образом, если п гораздо больше
вероятность того, что
для случайного выбора
незначительный.
На основе этого мы можем создать следующий эскиз протокола, чтобы проверить, имеет ли Алиса действительный набор назначений:
- Алиса выбирает полиномы
нет высшего порядка д . - Боб выбирает случайную точку
и вычисляет скрытие
. - Алиса отправляет Бобу поиск этих многочленов в точке с , а именно
. - Боб проверяет, выполняется ли требуемое равенство в точке с .
То есть он проверяет
Следовательно, Боб, скорее всего, отвергнет ответ Алисы независимо от выбора.
с .
Давайте подумаем, есть ли у нас инструменты для реализации этого эскиза? Важным моментом является то, что Алиса выбирает полиномы, которые она будет использовать, не зная с .
Но это именно та проблема, которую мы решили при истинной слепой полиномиальной оценке, описанной в предыдущая статья .
Имея это в виду, есть еще четыре основные вещи, которые необходимо решить, чтобы превратить этот эскиз в zk-SNARK. Первые два мы рассмотрим в этой статье, а оставшиеся два — в заключительной статье.
Уверенность в том, что Алиса выбирает свои полиномы в соответствии с набором присваиваний.
Важный момент: если у Алисы нет допустимого набора назначений, это не означает, что она не может найти любой полиномы
нет высшего порядка д , для которого
.
Это просто означает, что он не может найти полиномы, где
И
были «получены из набора заданий»; а именно, что
для набора персонала
.
Приведенный выше протокол гарантирует, что он использует только некоторые полиномы.
желаемый порядок, но не гарантирует, что они были созданы из допустимого набора назначений.
Формальное доказательство немного сложное, поэтому мы дадим приближенное решение.
Давайте объединим полиномы
в один полином Ф следующим образом:
Значение умножения р на
И О на
заключается в том, чтобы «не смешивать» коэффициенты
В Ф .
Шансы
В Ф вести переписку л , следующее
коэффициенты
вести переписку р , и последний
коэффициенты соответствуют О .
Объединим аналогичным образом полиномы в определении КАП, определяя для каждого
полиномиальный
чей первый
коэффициенты - это коэффициенты
, а затем коэффициенты
а потом
.
То есть для каждого
мы определяем полином:
Обратите внимание, что когда мы суммируем два
, Что
И
«подводится отдельно».
Например,
.
В более общем смысле, предположим, что у нас есть
для какого-то набора
.
Тогда мы также получим
по тем же коэффициентам
.
Другими словами, если Ф представляет собой линейную комбинацию
это означает, что
фактически были созданы из набора.
Поэтому Боб попросит Алису доказать ему, что Ф представляет собой линейную комбинацию
.
Это делается аналогично протоколу для достоверного расчета:
Боб выбирает случайный
и отправляет Алису прятаться
.
Затем он просит Алису прислать ему шкуру.
.
Если ей это удастся, Расширенная версия Знание принятого соотношения предполагает, что она знает, как создать Ф , который представляет собой линейную комбинацию
.
Добавление части с нулевым знанием: скрытие набора заданий
В zk-SNARK Алиса хочет скрыть всю информацию о своем наборе заданий.
Однако, скрывая
дайте некоторую информацию о наборе.
Например, при наличии некоторого другого удовлетворяющего набора присваиваний
Боб может вычислить соответствующее
и прячется
.
Если они отличаются от ответа Алисы, он может понять, что
не набор заданий Алисы.
Чтобы избежать такой утечки информации о своем наборе, Алиса скрывает свой набор, добавляя «случайный» Т -смещение» для каждого полинома, т.е.
выбирает случайный
Теги: #информационная безопасность #математика #криптовалюта #Децентрализованные сети #перевод #криптография #защита информации #zk-snarks
-
Обзор Synology Diskstation 211J
19 Oct, 24 -
Вр - Выпуск №37
19 Oct, 24


