«Поздно вечером три девушки крутились под окном».

Ну как они крутились.
Не крутились они, конечно, но понравились друг другу.
По условиям конкурса «Мисс Салтан» девушки должны были выбрать между собой лучшую.
«Какие-то странные соревнования», — забеспокоились девушки.
И это было правдой.
По правилам конкурса вес лайка участника зависел от того, сколько лайков он получил от других.
Что это значит, до конца не поняла ни одна из девушек.
«Как все сложно», — тосковали девчонки и подбадривали себя песней «Если бы я была королевой».
Вскоре «в комнату вошел король – государь той стороны» (показан на картине).
«В течение всего разговора.
» — ну, в общем, понятно.
«Собирая лайки нежности – формируя матрицу смежности», – весело рифмовал он.
Красивые девушки с именами Алена, Варвара и Софья смутились, но лайки (с балалайки) передали.
Вот что там было:
Алена получила 1 лайк от Софьи и 2 лайка от Варвары.Варвара получила лайк от Алены и Софьи.
А Софья получила 2 лайка от Алены и 1 от Варвары.
Царь взял лайки, крутил гайки, постучал колесами, принюхался, причмокнул, стиснул зубы, загнал их в палаты и объявил результаты.
Наибольший вес лайков получила Софья (7 баллов), но титул «Мисс Салтан» достался Алене (15 баллов).
Подробнее о подобной матрице Для матрицы
вектор потенциалов равен (5, 4, 7), а вектор потоков (15, 12, 14).
После объявления результатов девушки бросились к королю с просьбой рассказать ему, откуда взялись эти странные цифры?
1. Уравнение баланса
Наш мир основан на балансе.Это значит, что если что-то поступило в одно место, то такое же количество осталось в другом месте.
Физики демонстрируют этот баланс уравнение непрерывности для непрерывных и непрерывных сред. Но в современном мире танковые танки приводят в движение дискретные системы - графы.
В графе есть узлы, через которые течет поток (ну как он течет — рывками и нерегулярно).
Принцип баланса прост — в узле графа остается разница между тем, сколько из него утекло и сколько в него утекло.
Куда течет поток из узла? Правильно — в другие узлы, и соответственно поток также поступает в узел из других узлов.
Запишем этот набор слов по формуле:
Здесь
обозначает количество входящего потока в я й узел,
— величина потока, выходящего из узла,
— изменение баланса в узле.
Да, остатки в наших кошельках подчиняются этому уравнению баланса.
И на этом строится весь учет - даже названия специальные придумали: исходящий поток - кредит, входящий - дебет. Неизвестно, кто и почему ввел принцип равновесия в естественные (физические) системы, но лучше принцип равновесия положить в основу искусственных систем (учёта, рейтингов, кармы и т. д.).
Если мир выжил в балансе, то у такой системы есть шанс.
Во многих ситуациях (особенно при нашей рейтинговой конкуренции) учет баланса в узле не нужен.
То есть оно всегда ноль — сколько втекло, столько и вытекло.
Игра с нулевой стоимостью и нулевым остатком.
Для таких систем уравнение упрощается:
Прохладный.
Но пока от этого мало пользы.
Потенциальный баланс
Когда мы говорили о том, как поток может течь из узла я к узлу дж , мы подразумевали, что между этими узлами существует некоторая связь.В противном случае потоку просто не через что будет течь.
Связность узлов графа обычно называют матрица смежности (связности) , его элементы обозначаются
.
Применительно к потокам матрицу смежности еще называют матрица проводимости .
Его элементы отражают пропускная способность ребра графа.
Есть связь — есть поток, нет связи — нет потока.
Логично предположить, что чем прочнее связь, тем больше поток.
Таким образом, поток между узлами пропорционален размеру соединения узлов.
Но что такое коэффициент пропорциональности? Ответ будет немного расплывчатым – поток из узла пропорционален определенному потенциал узла .
Суть этого ответа в том, что узлы имеют некоторый потенциал.
и этот потенциал напрямую определяет величину выходящего потока.
Если, например, у нас есть два узла, то проводимость между ними одинакова в обоих направлениях (
), то суммарный поток между узлами будет определяться разностью потенциалов этих узлов.
Существование электрических сетей доказывает, что это действительно работает.
Связь между потоком, потенциалами и проводимостью выражается простой формулой:
Подставив (1.3) в уравнение баланса (1.2), получим систему уравнений для расчета узловых потенциалов:
В этом уравнении известными являются проводимости, а неизвестными — потенциалы.
Количество уравнений в системе равно количеству узлов графа.
Решение системы уравнений баланса является непосредственной задачей расчета потенциалов (и потоков) графа.
В уравнении (1.4) мы использовали понятие суммарной проводимости соединений, исходящих из узла – степени узла:
Рейтинги и самооценки
«Это все здорово», — сказали девочки, зевая.— «Но какое отношение это имеет к лайкамЭ» В системах голосования, в которых участники оценивают друг друга, рейтинги основаны на весе голоса каждого участника.
И вес голоса опять же зависит от того, как оценили этого участника другие.
Соединение с потоками.
Когда я -й участник с голосовым весом
оценивает дж -й участник с рейтингом (количество лайков)
затем он делится с ним своим потоком
.
Здесь нет смысла накапливать остатки, поэтому каждый участник делится с остальными всем, что получает.
Вес голоса участника является потенциальным
, матрица лайков — это матрица смежности (связности), а итоговый балл — это общий полученный (он же отправленный) поток
.
Чтобы ранжировать участников (определить лучших), нам необходимо решить уравнение баланса (1.4), то есть определить веса участников, которые будут балансировать систему.
2. Лапласианы
Когда я был молод и глуп, я впервые столкнулся с уравнением баланса (1.4), я уже умел программировать и знал о циклах.Поэтому я решил это как программист — методом последовательных итераций.
Задаем исходный вектор потенциалов, умножаем его на матрицу смежности, делим на степени узлов, получаем новый вектор потенциалов и т. д. Как правило, процесс сходится.
А о своей молодости я вспомнил после прочтения статьи о ценности пьяницы , что, в общем-то, и побудило меня «открыть формулы».
Помню «вау-эффект», когда узнал, что есть еще один способ расчета потенциалов, о котором, видимо, знали наши деды Лаплас и Кирхгоф.
Метод основан на свойствах матриц Лапласа.
Здесь уже недавно вспомнил Лапласиан в сплошных средах.
Дискретные лапласианы не менее интересны и важны.
Чтобы определить матрицу Лапласа по заданной матрице смежности, мы используем приведенное выше понятие степени узла.
Степени узлов расположим по диагонали лапласиана, а остальные элементы из матрицы смежности возьмем с противоположным знаком.
Полученную матрицу еще называют Матрица Кирхгофа :
Здесь вы можете увидеть лапласиан из наших лайков
Предположим, что проводимость узлов, исходящих из я дуга указана в я й столбец матрицы.
Соответственно, в я Четвертая строка матрицы — проводимость дуг, входящих в узел.
Тогда сумма элементов каждого столбца лапласиана равна нулю.
Вообще говоря, матрицы этого типа образуют отдельный класс — лапласианцы .
Определитель лапласианов всегда равен нулю, поэтому для них, например, не существует обычной обратной матрицы.
Но есть еще одна (псевдо) обратная, там тоже своя единичная матрица.
Лапласиан можно получить не только указанным выше преобразованием.
Например, преобразование отклонений также дает результат Лапласа.
Лапласианы могут быть симметричными — в них потенциалы всех узлов равны друг другу — для нашей задачи они пока не интересны.
Матрица Кирхгофа относится к классу лапласианов.
Лапласовы потенциалы
В линейной алгебре есть понятие дополнительный минор (кофактор) матрица — определитель матрицы, полученный из оригинала путем удаления строк и столбцов (с учетом знака).Кофакторы играют большую роль в лапласианах.
Потенциал 1-го порядка лапласиана — это определитель матрицы, полученной удалением одной строки и одного столбца из исходного лапласиана.
Поскольку мы предполагали, что в наших лапласианах сумма каждого столбца равна нулю, значение потенциала определяется только зачеркнутым столбцом — строка может быть любой.
Удобно зачеркнуть ту же строку, что и столбик – тогда не придется думать о знаке определителя.
Итак, если мы обозначим через
дополнительный минор матрицы, то определение потенциала Лапласа можно записать в виде
Таким образом, эти потенциалы 1-го порядка из матрицы Кирхгофа являются искомым решением уравнения (1.4).
Чудесный.
Никаких циклов, начальных присвоений, матричных произведений и т. д. не требуется.
Я удалил строку/столбец, вычислил определитель и получил ответ. Свойства потенциалов 1-го порядка Потенциал узла — это сумма произведений (кортежей) проводимостей ребер графа по всем возможным путям к данному узлу, исключая контуры (циклы).
Количество факторов в произведении на 1 меньше размерности (количества узлов) графа.
Потенциал узла не зависит от проводимости исходящих от него дуг.
Каждый кортеж (путь) в выражении потенциала узла состоит из дуг, исходящих из всех узлов, кроме этого.
В одном кортеже не бывает двух дуг, исходящих из одного узла, но могут быть дуги, входящие в один и тот же узел.
Каждый кортеж (путь) должен содержать дугу, входящую в узел (замкнутость).
Выражение для потенциала не содержит кортежей, содержащих циклы (схемы).
Число кортежей в выражении для потенциала определяется известной формулой Кэли
и быстро растет по мере роста узлов графа.
Для 4 узлов имеем 4^2 = 16 термов, для пяти — 5^3 = 125 и т.д. В симметричном графе потенциалы всех узлов равны — следствие того, что структура выражения для потенциалов всех узлов одинакова (разница лишь в направлении).
Графическая структура потенциала графа из 4 узлов Демонстрирует комбинаторную природу выражения для потенциала.
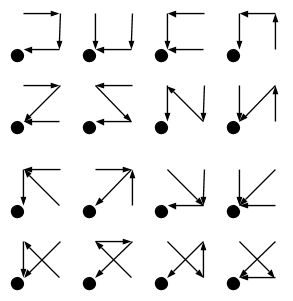
Чтобы определить расход через узел, достаточно потенциал узла умножить на его степень:
Мы получили то, что хотели.
Подсчет лайков Для расчета веса голоса (потенциала) участника зачеркните соответствующую строку и столбец и вычислите определитель.
Получаем 3 потенциала:
Это вес голоса каждого участника.
Теперь посчитаем стримы и определим, кто сколько голосов набрал:
Алена получила наибольшее количество голосов.
Как рассчитать потенциалы больших графов
Если граф большой (много узлов), то вычисление вектора потенциала путем вычисления определителей миноров лапласиана неудобно (затратно).В таких ситуациях лучше использовать обращение матрицы.
Алгоритм следующий: В матрице Лапласа заменим первую строку вектором (1, 0, 0, .
).
Вычисляем обратную матрицу полученной и находим ее определитель.
Делим значения первого столбца полученной обратной матрицы на ее определитель.
Это и есть искомый вектор потенциалов.
В первой строке записан потенциал первого узла, во второй – второго и т.д. Если абсолютное значение потенциала не имеет значения, то считать и делить на определитель не нужно.
Ранжирование объектов по потенциалам и потокам
По результатам нашего примера получилось, что наибольший вес голосов получила Софья, а вот Алёна набрала больше всего баллов.Это значит, что авторитетный и избранный – не одно и то же.
Что именно должно служить основой ранжирования – потенциалы или потоки – требует отдельного рассмотрения в каждой задаче, поскольку определяется прикладным аспектом.
Результаты турнира
Рассмотрим использование рейтинговой системы применительно к определению результатов шахматного турнира.Справедлива ли нынешняя система определения победителя, основанная на простой сумме очков? На наш взгляд, у него есть только одно преимущество – простота.
Но кого в эпоху смартфонов волнует простота? Несправедливо, что выигрыш сильного в «простой системе» по сути эквивалентен выигрышу слабого.
Современный и правильный подход – считать взвешенные точки, то есть использовать расчет потенциалов и потоков.
Еще один плюс в том, что при такой системе практически исключено разделение мест – не придется думать, что делать, если баллы равны.
Недавно В Москве завершился турнир претендентов.
(поздравляем Сергея Карякина с победой!), по итогам которого большое количество участников поделили места (2-3, 4-7).
Используя потенциальный метод, попробуем разобраться, кто какое место на самом деле занял.
Результаты турнира представляют собой матрицу смежности графа.
С точки зрения лайков потеря участника — это всё равно, что поставить лайк победителю (хотя это звучит немного непривычно).
Происходит поток взвешенных очков от проигравшего к победителю.
Каков потенциал по отношению к игрокам? Потенциал – это сила игры, проявленная участником (в данном турнире).
Чем выше потенциал участника, тем больше ценность полученных от него очков для других.
Может ли более слабый игрок набрать больше очков, чем более сильный? Да, это вполне возможно, хотя и случается не так часто.
Например, на вышеупомянутом турнире претендентов сила участника и набранные им очки совпали – рейтинг по потенциалам и потокам оказался равноценным.
Для интересующихся подробностями Мы нормировали потенциалы и потоки так, чтобы их сумма была равна 100. Сергей Карякин Хикару Накамура Аниш Гири Виши Ананд Веселин Топалов Левон Аронян Фабиано Каруана Петр Свидлер ты 17,8 11,4 12,5 13,7 6,4 12,0 13,8 12,4 Дж 14,5 11,8 13,0 13,2 9,0 12,4 13,3 12,8 М 1 7 4 3 8 6 2 5 Каруана по-прежнему второй, а Гири – четвертый.
Потенциал пьяницы
Последний пример, который мы рассмотрим в этой статье, — это расчет значения карт в народной игре «Пьяница».Спасибо за этот пример астма .
Без него статьи , возможно, и этого не существовало бы.
Подробности о постановке задачи - в упомянутой статье - карты бьют друг друга по правилам старшинства, но при этом шестерка бьет туза.
Эта задача хороша тем, что потенциальные значения (хм, а что здесь означают потоки?) можно выразить явно — с помощью простых формул.
Общий вид матрицы смежности соответствует результатам сравнения карт – кто кого бьет.
Пронумеровав карты от условного туза до условной шестерки, получим следующий вид матрицы смежности:
Ключевая особенность находится в левом нижнем (и/или правом верхнем) углу — «шесть битов туз».
Тогда матрица Кирхгофа будет иметь вид:
Теперь вам ясно видно, почему потенциал «шестерки» равен (n-2)! Потому что, вычеркивая столбец и строку, соответствующие «шестерке» (это крайние строки справа и снизу), мы получаем треугольную матрицу, определителем которой считается простое перемножение элементов основной диагональ.
То же самое справедливо и для Туза (1-я строка и столбец), с той лишь разницей, что элемент (n-2) появляется в его множителях дважды.
Поэтому сразу понятно, что потенциал туза всегда (n-2) раз превышает потенциал шестерки.
Сводка формул Выражения для потенциалов от Туза до Шестерки:
Интересно, что сумма потенциалов всех карт (кроме шестерки и туза) равна потенциалу туза:
Заключение
Девочки как могли старались и слушали рассказ царя Салтана о возможностях Лапласа, но все равно уснули глубоким сном.Они мечтали о молодцах с большим потенциалом, управляющих большими потоками.
Пришло время нам положить этому конец.
Используйте свои возможности! Теги: #рейтинг #рейтинги #баланс #уравнение непрерывности #матрица Лапласа #потенциалы #Алгоритмы #математика

-
Как Я Стал Дизайнером За Полгода
19 Oct, 24 -
Реалии Миграции Sharepoint В Облако
19 Oct, 24


