В задачах управления бывают случаи, когда известен закон движения объекта управления и необходимо разработать регулятор с определенными характеристиками.
Иногда задача усложняется тем, что уравнения, описывающие объект управления, оказываются нелинейными, что усложняет конструкцию регулятора.
В связи с этим разработано несколько методов учета нелинейных особенностей структуры объекта управления, одним из которых является метод обратной задачи динамики.

Введение
Метод обратной задачи динамики естественным образом возникает при попытке «преобразования» одной динамической системы в другую, когда разработчик имеет два уравнения, одно из которых описывает существующую управляемую систему, а другое выражает закон движения этой самой управляемой системы, превращая это во что-то полезное.Закон может выглядеть по-другому, но главное, чтобы он был физически реализуем.
Это может быть закон синусоидального изменения напряжения на выходе генератора или системы автоматического регулирования частоты, закон скорости вращения турбины или движения каретки принтера, а может быть даже икс, Координаты Y грифеля карандаша, которым манипулятор подписывает открытки.
Однако «навязать» свой закон управления, укладывающийся в рамки физической реализуемости и управляемости объекта, можно различными способами, и это зачастую не самая сложная часть разработки.
Но то, что рассматриваемый метод позволяет достаточно легко учесть нелинейность и многомерность объекта, на мой взгляд, повышает его привлекательность.
Кстати, здесь можно заметить связь с методом компенсации нелинейности по обратной связи [1].
Известно, что в ряде случаев правильно составленные нелинейные регуляторы даже при управлении линейной системой обеспечивают лучшие характеристики управления по сравнению с линейными регуляторами [2].
Примером может служить регулятор, уменьшающий коэффициент демпфирования системы при увеличении ошибки выполнения команды и увеличивающий его при уменьшении ошибки, что приводит к улучшению качества переходного процесса.
Вообще говоря, тема управления, связанная с необходимостью учета нелинейностей, давно привлекает внимание ученых и инженеров, поскольку большинство реальных объектов до сих пор описываются нелинейными уравнениями.
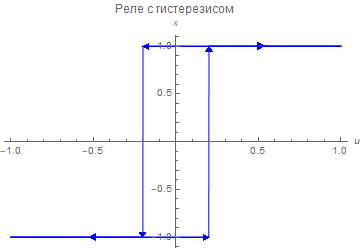
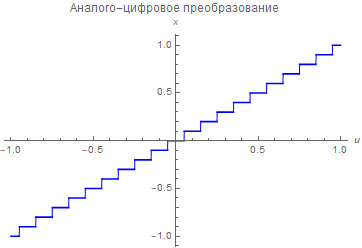
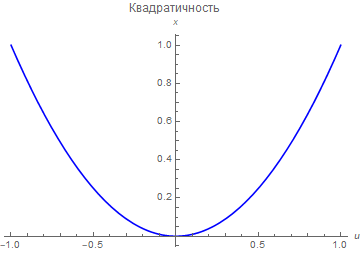
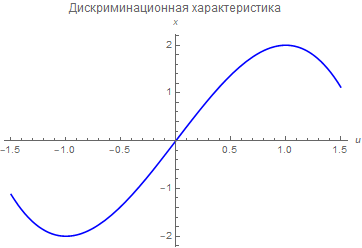
Вот несколько примеров нелинейностей, часто встречающихся в технике:
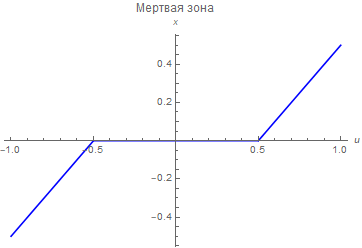 |
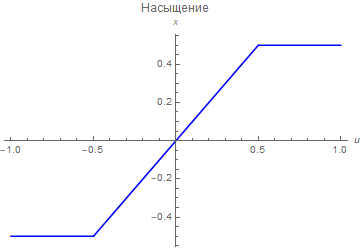 |
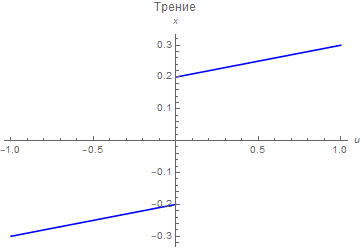 |
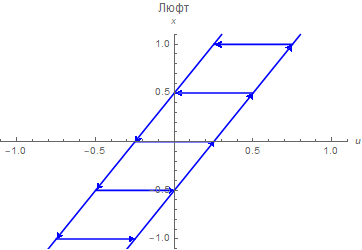 |
 |
 |
 |
 |
Пусть имеется объект управления, который можно описать в виде дифференциального уравнения n-го порядка.
в котором есть негодование
(это может быть шум измерительного прибора, внешнее случайное воздействие, вибрация и т.п.
) и управляющий сигнал
(в технике управление чаще всего осуществляется с помощью напряжения).
В этом случае для простоты восприятия мы рассматриваем одномерный объект управления, включающий в себя одно возмущение.
В общем случае эти величины являются векторными величинами.
Предполагается, что фазовые переменные
, которые описывают состояние объекта управления, возмущения
и управление
зависят от времени, но для удобства восприятия этот факт не показан.
Выражение (1) может содержать нелинейности, а также быть нестационарным, т.е.
параметры которого явно изменяются со временем.
Примером нестационарного уравнения может быть количество ядер урана в реакторе, которое постоянно уменьшается в результате реакции распада, что приводит к непрерывному изменению оптимального закона управления стержнями-замедлителями.
Регулятор построен таким образом, чтобы выработать известный ранее закон управления, который может быть описан дифференциальным уравнением порядка не ниже порядка уравнения (1), описывающего объект управления:
Где
– сигнал управления и его производные в количестве, позволяющем полностью описать требуемый закон управления.
Таким образом, для системы стабилизации нет необходимости измерять производные управления.
Для системы слежения за линейно меняющимся входным сигналом достаточно измерить первую производную.
Чтобы отслеживать квадратично меняющийся сигнал, вам придется добавить вторую производную и так далее.
Следует отметить, что этот сигнал подается на вход контроллера, в отличие от сигнала
, поступающий на вход объекта управления от регулятора.
Это уравнение также может быть как нелинейным, так и нестационарным.
Для определения необходимого управляющего сигнала
Выразим из (2) старшую производную
и подставим вместо него полученное выражение
в уравнение (1), выражающее управление:
Из выражения (3) становится ясно, что для создания требуемого управляющего сигнала необходимо помимо внешних возмущений (если их влияние существенно) измерять и саму контролируемую величину.
, и все его производные до порядка
включительно, что может вызвать некоторые трудности.
Во-первых, высшие производные могут быть недоступны для прямого измерения, как, скажем, производная ускорения, в результате чего придется прибегать к операции дифференцирования либо программно, либо схемотехнически.
А этого, как известно, стараются избегать из-за повышенного шума.
Во-вторых, измерения неизбежно содержат шум, и это вынуждает прибегать к фильтрации.
Любой фильтр является динамическим или, другими словами, инерционным элементом, что означает наличие производной в уравнении.
Следовательно, порядок всей системы управления в общем случае увеличится на число, равное сумме порядков уравнений, описывающих все фильтр-измерители.
То есть, если мы управляем объектом второго порядка и в каждом канале измерения используем фильтры второго порядка для измерения выходной величины и ее производной (то есть всего два фильтра второго порядка), то порядок системы управления увеличится.
на четыре.
Конечно, если постоянные времени фильтра достаточно малы, то влиянием сглаживающих элементов можно пренебречь.
Но в любом случае они введут в систему так называемые малые динамические параметры и их совокупный вклад может повлиять на устойчивость системы управления в целом [2].
Следует также понимать, что данный метод позволяет задать управление только в переходном процессе и не связан с оптимизацией по какому-либо критерию качества управления.
Связь между контроллером и объектом управления можно описать следующей схемой: 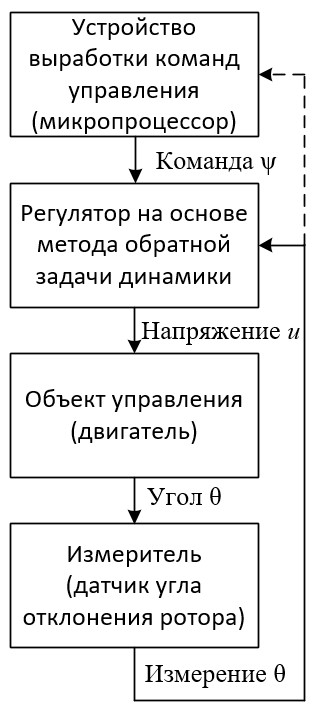
Управление генератором Ван дер Поля
Рассмотрим пример синтеза регулятора для управления автоколебательной системой.
Это вымышленный пример, хорошо объясняющий суть метода.
Предположим, вы хотите управлять системой, уравнение которой выглядит следующим образом:
Закон управления должен быть таким:
Где
– наш главный управляющий сигнал (уставка).
То есть, по сути, мы хотим «превратить» наш генератор с нелинейностью в линейный колебательный агрегат. Следует отметить, что там же [2] данная система является системой стабилизации, поскольку выходной сигнал
имеет тенденцию повторять входной сигнал
, то есть стабилизирует выходную мощность системы на заданном постоянном уровне
, который может быть отображен как
Важно, чтобы входной командный сигнал
был постоянным или медленно менялся (настолько медленно, что ошибка запаздывания
от
укладываются в наши требования к точности) величиной или кусочно-постоянной функцией, так как вся система имеет астатизм 0-го порядка (т. е.
статична) и для любого постоянно меняющегося задающего сигнала
на выходе системы обязательно появится динамическая ошибка, которая будет выглядеть как прибавление к выходному значению некоторой постоянной величины, монотонно зависящей от скорости изменения управляющего воздействия.
Эта функция будет устранена в будущем.
Итак, выразим старшую производную из уравнения (5):
и подставим его в (4), выразив
:
Это сигнал управления, который будет генерироваться регулятором из требуемого сигнала управления.
.
Из (6) также следует, что необходимо измерить выходную величину
и его первая производная.
Автоколебания генератора Ван дер Поля с параметрами
выглядеть так: 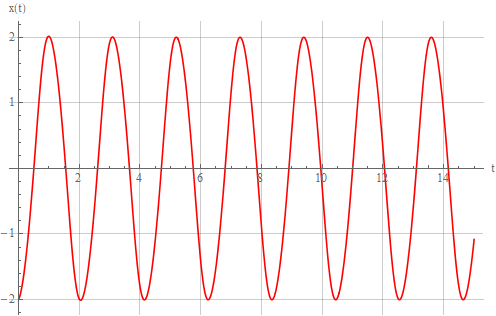
Пусть у нас есть управляющий сигнал «ступенчатого» типа: 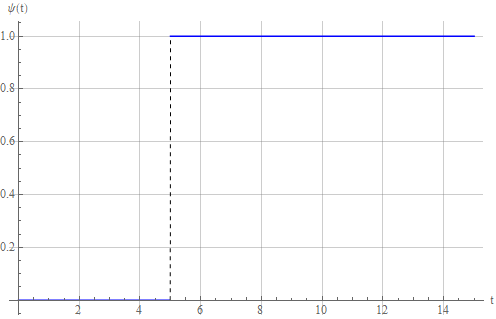
и мы хотим, чтобы система повторила это.
Давайте применим его ко входу генератора и посмотрим на ответ: 
Под воздействием единственного входного сигнала к колебаниям генератора добавлялось лишь небольшое постоянное смещение.
Предположим теперь, что нам необходимо получить реакцию генератора на задающий сигнал, соответствующую реакции колебательного элемента (5), с постоянной времени
и коэффициент демпфирования
.
Ответ
такая колебательная единица на единицу шага представлена ниже: 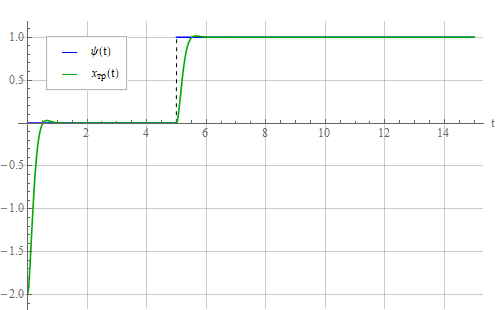
Теперь подадим управляющий сигнал на осциллятор.
, описываемый выражением (6): 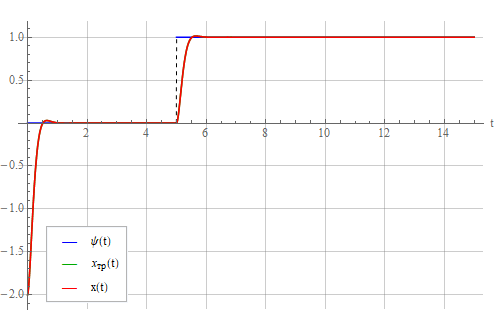
Видно, что осциллятор ведет себя в соответствии с требуемым законом.
Давайте посмотрим на управляющий сигнал.
: 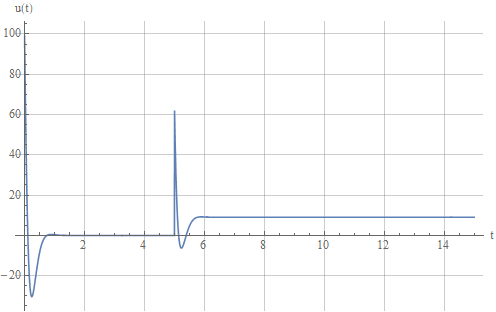
На рисунке видно значительное перерегулирование во время переходного процесса.
В реальной системе, скорее всего, либо система уйдет в насыщение (разрушение), либо, чтобы этого не допустить, придется ограничить входной сигнал.
Учтем это, ограничив амплитуду управляющего воздействия
на уровне
15. Сигнал управления теперь выглядит так: 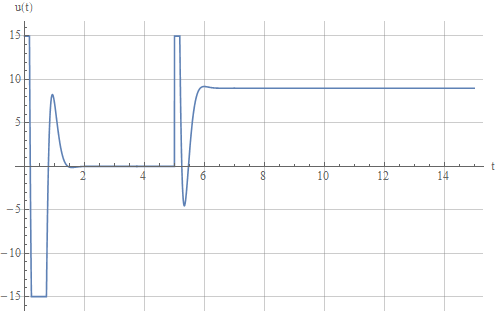
и выходной сигнал генератора: 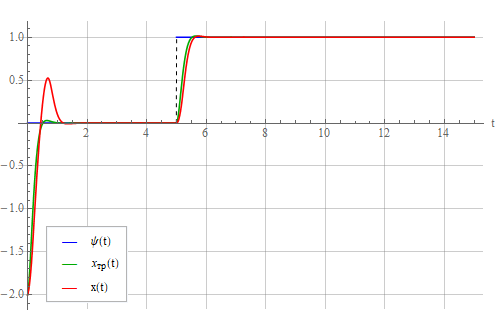
Последствия ограничения сигнала - b О Наименьшая переходная ошибка, которая в зависимости от желаемых свойств системы может быть весьма значительной.
По мере увеличения требуемой постоянной времени переходные излучения уменьшаются.
Нужно следить, чтобы максимальный управляющий сигнал в установившемся режиме (который на этом графике начинается примерно с шестой секунды) не был ограничен, иначе будет бесконечный переходный процесс и система не выполнит поставленную задачу.
Коэффициент усиления контроллера, то есть коэффициент управляющего сигнала
на выходе регулятора опорного действия
определяется параметрами управляемой системы, а именно множителем
.
Теперь давайте подадим на вход генератора следующий линейно изменяющийся сигнал: 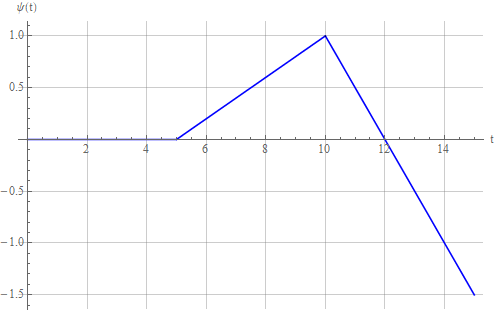
Реакция колебательного звена: 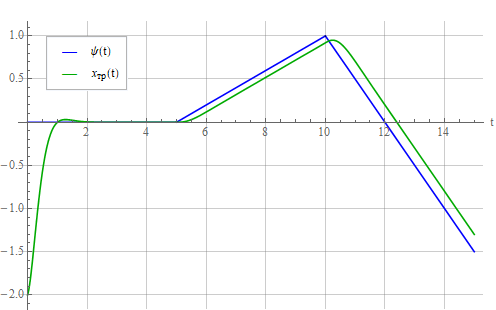
и осциллятор: 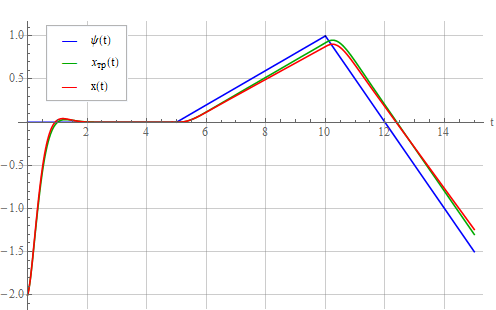
Видно, что появилась постоянная задержка - динамическая ошибка, поскольку система рассчитана на отслеживание только постоянного ведущего сигнала.
.
Чтобы иметь возможность отслеживать даже линейно меняющийся сигнал, необходимо оценить скорость его изменения и учесть ее в контроллере.
Для этого составим необходимый закон управления следующим образом:
Где
– ошибка отслеживания задающего сигнала генератором.
Выразим также старшую производную из (7), подставим ее в уравнение объекта управления (4) и получим управляющий сигнал:
В новой структуре регулятора, соответствующей выражению (8), появилась скорость изменения задающего воздействия
.
Давайте посмотрим на выход системы, когда на вход подается линейно меняющееся опорное воздействие: 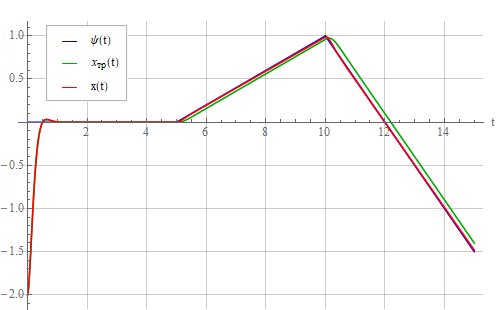
Генератор отслеживает опорный сигнал
.
Но это полностью синтетический пример.
В действительности будет система, структура которой, возможно, не определена достаточно точно — это одно.
Параметры системы мы также определим с определенной погрешностью – это два.
Управление включает фазовые переменные
, которые придется измерять с некоторым шумом – это три.
Причем параметры системы могут со временем уходить, то есть стационарная система в течение достаточно длительного периода времени может проявлять нестационарное поведение.
Хотя правильнее было бы сказать так: за достаточно короткий промежуток времени нестационарная система может показаться стационарной.
В данном примере будем считать, что система идентифицирована с достаточной точностью и ее изменение во времени весьма незначительно.
Тогда для наглядности перепишем выражение регулятора (6) следующим образом:
Где
– измеряемая регулируемая переменная и ее производная;
– идентифицированные собственная частота и коэффициент нелинейного затухания соответственно.
Добавим 10% ошибку в определении параметров осциллятора, положив
.
Посмотрим на результат: 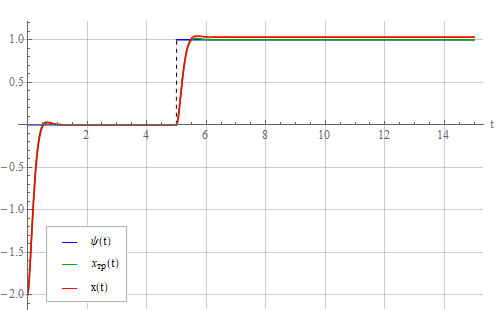
На рисунке видно, что появилась статическая ошибка, которая растет с увеличением ошибки идентификации.
и в установившемся режиме не зависит от погрешности
.
Но последнее влияет на отклонение переходного процесса генератора от такового для идеального колебательного элемента.
Можно попробовать сделать то же, что и при проектировании ПИД-регуляторов ( Хабр И не Хабр ) – добавляем к управляющему сигналу интеграл ошибки (не забывая про интеграл насыщения один раз , два ).
Но опустим пока этот вопрос и рассмотрим выражение (9), из которого видно, что чем меньше собственная частота
по сравнению с требуемой постоянной времени
, тем меньше влияние ошибки идентификации одного и того же
.
Давайте уменьшим
от 0,125 до 0,05. Статическая ошибка также уменьшилась: 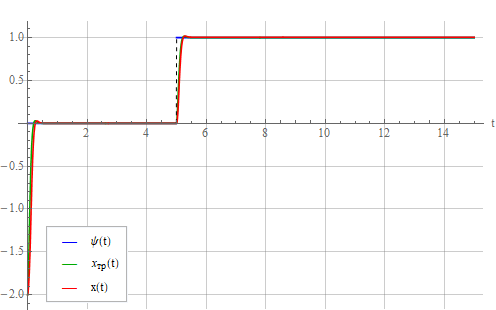
Теперь попробуем компенсировать статическую погрешность, добавив к регулятору интеграл от погрешности.
(как в ПИ-регуляторе).
Выражение (9) превратится в
Где
– коэффициент интегральной составляющей;
- Текущее время.
Интеграл здесь записан формально как поясняющий общую идею, а не математическое описание конкретного алгоритма, поскольку в реальном контроллере необходимо принимать меры по ограничению накапливаемой погрешности, иначе могут возникнуть проблемы с переходным процессом.
Посмотрим на реакцию системы под воздействием результирующего регулятора, соответствующего выражению (10): 
На рисунке видно, что статическая ошибка со временем уменьшается, но переходный процесс запаздывает. По аналогии с ПИД-регулятором можно попробовать добавить пропорциональную и дифференцирующую составляющие.
Результат был такой (коэффициенты подбирались не особо тщательно): 
Естественно, сложение интегральной и дифференциальной составляющих уже не является частью метода обратной задачи динамики, а реализует некий метод оптимизации переходного процесса.
Проанализируем влияние переменного шума измерения.
.
Давайте снова применим шаг ко входу системы и посмотрим на выход при отсутствии каких-либо шумов (ошибка идентификации все та же 10%): 
Теперь добавим размеры
белый гауссов шум с нулевым математическим ожиданием и равными дисперсиями
, прошедший через апериодические связи с постоянными времени
, которые имитируют измерительный датчик+ ФНЧ .
Одна из получившихся реализаций шума: 
Теперь вывод системы тоже начал шуметь: 
в результате зашумленного управляющего сигнала:
Давайте посмотрим на ошибку обработки задачи: 
Попробуем увеличить постоянные времени датчиков.
и снова посмотрите на вывод системы: 
Появились значительные колебания – результат действия тех самых неучтенных малых динамических параметров [2], которые описывают датчики (их инерционность).
Эти динамические параметры затрудняют фильтрацию шума, вынуждая описывать датчики с «большими» постоянными времени, что, вообще говоря, не всегда может дать положительный результат. Контроль двигателя Теги: #математика #Алгоритмы #двигатели #Анализ и проектирование систем #управление #схемотехника #ПИД-регулятор #динамические системы

-
Номер Службы Поддержки Клиентов Windows 10
19 Oct, 24 -
Проблемы С Обновленным App Store
19 Oct, 24 -
Быстрый Доступ К Оснасткам Windows
19 Oct, 24


