Всем привет. Эта неделя в курсе машинное обучение Профессор Эндрю Нг рассказал слушателям о метод главных компонент , который можно использовать для уменьшения размерности пространства признаков ваших данных.
Но к сожалению, он не рассказал о методе вычисления собственных векторов и собственных значений матрицы, просто сказал, что это сложно и посоветовал использовать функцию Matlab/octave [U S V] = svd(a).
Для моего проекта мне нужна была реализация этого метода на C#, чем я и занимался сегодня.
Сам метод главных компонент очень изящный и красивый, и если не понимать математику, которая за всем этим стоит, то это все можно назвать шаманством.
Проблема с вычислением собственных векторов матрицы состоит в том, что нет быстрый способ вычислить их точные значения, так что вам придется уйти.
Я хочу рассказать об одном из таких способов выхода, а также приведу C#-код, выполняющий эту процедуру.
Пожалуйста под кат. Метод главных компонентов (кода пока нет) Часть первая: инициализация алгоритма.
Входными данными алгоритма является массив данных, а также размерность пространства, до которого необходимо свести данные.
- Рассчитано ковариационная матрица (у этой матрицы есть замечательное свойство — она симметрична, это нам очень пригодится)
- Собственные векторы матрицы вычисляются
- Выбираются первые собственные векторы en, где en — та самая размерность, до которой необходимо привести размерность пространства признаков; выбранные векторы можно записать вертикально и собрать в матрицу

Входные данные — вектор тех же размеров, что и массив данных, используемый на этапе инициализации; выходной сигнал представляет собой вектор меньшей размерности (или проекцию входного вектора на ортонормированный базис, образованный выбором собственных векторов).
- Умножив входной вектор скалярно на все векторы из выборки собственных векторов, получим уменьшился вектор:

Входными данными является вектор размерности, равный тому, которому мы уменьшенный векторы; Выходные данные представляют собой вектор исходного измерения.
- Если мы транспонируем матрицу

тогда он будет содержать то же количество строк, что и размерность входного вектора на предыдущем шаге, а искомый вектор восстанавливается по формуле:
Я не буду подробно останавливаться на расчете ковариационной матрицы, поскольку она по определению рассчитывается наивно.
Изучив несколько алгоритмов вычисления собственных векторов матрицы, я остановился на итерационном методе QR-декомпозиции.
Имеет существенное ограничение, более-менее точный результат выдает только для симметричных матриц, но нам повезло :), ковариационная матрица именно такая.
Второе ограничение этого алгоритма состоит в том, что матрица должна быть полноранговый .
QR-разложение Итерационный QR-метод для поиска собственных векторов, очевидно, использует QR-разложение , поэтому сначала вам придется реализовать этот процесс.
Для реализации этого процесса был выбран алгоритм Грэм-Шмидт .
Для этого нам понадобится функция, вычисляющая проекцию вектора а векторизировать б : 
, где <> - обозначаем скалярное произведение векторов.
Я не буду останавливаться на еще более простых функциях, таких как ScalarVectorProduct, чтобы размер кода в тексте не превышал критическую норму.public static double[] VectorProjection(double[] a, double[] b) { double k = ScalarVectorProduct(a, b)/ScalarVectorProduct(b, b); return ScalarToVectorProduct(k, b); }
Итак, сама процедура разложения QR IList РазложениеGS(double[][] a) получает на вход матрицу и выводит в ответ две матрицы:
- первый содержит в своих столбцах ортонормированный базис такой, что
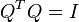
; - вторая матрица будет верхний треугольный .
List<double[]> av = new List<double[]>();
foreach (double[] vector in DecomposeMatrixToColumnVectors(a))
{
av.Add(vector);
}
Инициализируем два вспомогательных списка:
List<double[]> u = new List<double[]>();
u.Add(av[0]);
List<double[]> e = new List<double[]>();
e.Add(ScalarToVectorProduct(1 / NormOfVector(u[0]), u[0]));
Это те же одноименные списки, которые используются в схеме алгоритма:
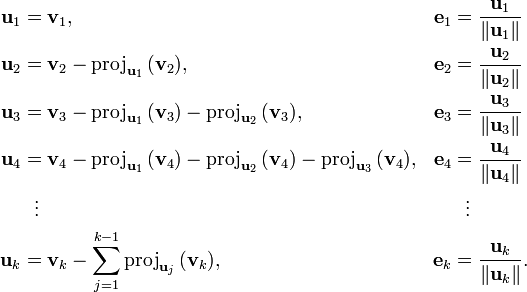
После инициализации первый ты И е мы рассчитали, мы продолжаем цикл для расчета следующих значений:
for (int i = 1; i < a.Length; i++)
{
double[] projAcc = new double[a.Length];
for (int j = 0; j < projAcc.Length; j++)
{
projAcc[j] = 0;
}
for (int j = 0; j < i; j++)
{
double[] proj = VectorProjection(av[i], e[j]);
for (int k = 0; k < projAcc.Length; k++)
{
projAcc[k] += proj[k];
}
}
double[] ui = new double[a.Length];
for (int j = 0; j < ui.Length; j++)
{
ui[j] = a[j][i] - projAcc[j];
}
u.Add(ui);
e.Add(ScalarToVectorProduct(1/NormOfVector(u[i]), u[i]));
}
И, наконец, мы генерируем данные в выходном формате:
double[][] q = new double[a.Length][];
for (int i = 0; i < q.Length; i++)
{
q[i] = new double[a.Length];
for (int j = 0; j < q[i].
Length; j++)
{
q[i][j] = e[j][i];
}
}
double[][] r = new double[a.Length][];
for (int i = 0; i < r.Length; i++)
{
r[i] = new double[a.Length];
for (int j = 0; j < r[i].
Length; j++)
{
if (i >= j)
{
r[i][j] = ScalarVectorProduct(e[j], av[i]);
}
else {
r[i][j] = 0;
}
}
}
r = Transpose(r);
List<double[][]> res = new List<double[][]>();
res.Add(q);
res.Add(r);
return res;
Ура! Теперь нам нужен тест для этого:
[Test(Description = "Test of QRDecompositionGS")]
public void QRDecompositionGSTest()
{
double[][] a = new double[][]
{
new double[] {12, -51, 4},
new double[] {6, 167, -68},
new double[] {-4, 24, -41}
};
IList<double[][]> res = LinearAlgebra.QRDecompositionGS(a);
double[][] expQ = new double[][]
{
new double[] {6.0/7, -69.0/175, -58.0/175},
new double[] {3.0/7, 158.0/175, 6.0/175},
new double[] {-2.0/7, 6.0/35, -33.0/35}
};
double[][] expR = new double[][]
{
new double[] {14, 21, -14},
new double[] {0, 175, -70},
new double[] {0, 0, 35}
};
Assert.True(Helper.AreEqualMatrices(expQ, res[0], 0.0001), "expQ != Q");
Assert.True(Helper.AreEqualMatrices(expR, res[1], 0.0001), "expR != R");
}
Функция Helper.AreEqualMatrices сравнивает матрицы поэлементно до третьего параметра.
Итерационный метод QR
Итерационный метод QR основан на замечательной теореме, суть которой состоит в том, что если мы инициализируем матрицу A нулем как
и повторяйте следующий процесс бесконечно:
Другими словами, поскольку число итераций стремится к бесконечности, произведение
будет стремиться к точным значениям собственных векторов.
В то же время последний
будет содержать на главной диагонали собственные значения матрицы, приближенные конечно.
Напомню, что этот алгоритм более-менее точно работает только для симметричных матриц.
Итак, метод QR-итерации IList EigenVectorValuesExtractionQRIterative(double[][] a, двойная точность, int maxIterations) получает входные данные от самой матрицы, а также еще несколько параметров:
- двойная точность — точность, которую мы хотим достичь, алгоритм остановится, если изменения значений собственных векторов будут не больше этой величины;
- int maxIterations — максимальное количество итераций.
- первый содержит в своих столбцах собственные векторы матрицы а ;
- вторая матрица на своей главной диагонали содержит собственные значения матрицы а .
double[][] aItr = a;
double[][] q = null;
И давайте запускать цикл до тех пор, пока алгоритм не остановится:
for (int i = 0; i < maxIterations; i++)
{
IList<double[][]> qr = QRDecompositionGS(aItr);
aItr = MatricesProduct(qr[1], qr[0]);
if (q == null)
{
q = qr[0];
}
else {
double[][] qNew = MatricesProduct(q, qr[0]);
bool accuracyAcheived = true;
for (int n = 0; n < q.Length; n++)
{
for (int m = 0; m < q[n].
Length; m++)
{
if (Math.Abs(Math.Abs(qNew[n][m]) - Math.Abs(q[n][m])) > accuracy)
{
accuracyAcheived = false;
break;
}
}
if (!accuracyAcheived)
{
break;
}
}
q = qNew;
if (accuracyAcheived)
{
break;
}
}
}
Сгенерируем выходные данные:
List<double[][]> res = new List<double[][]>();
res.Add(q);
res.Add(aItr);
return res;
И конечно тест:
[Test(Description = "Test of Eigen vectors extraction")]
public void EigenVectorExtraction()
{
double[][] a = new double[][]
{
new double[] {1, 2, 4},
new double[] {2, 9, 8},
new double[] {4, 8, 2}
};
IList<double[][]> ev = LinearAlgebra.EigenVectorValuesExtractionQRIterative(a, 0.001, 1000);
double expEV00 = 15.2964;
double expEV11 = 4.3487;
double expEV22 = 1.0523;
Assert.AreEqual(expEV00, Math.Round(Math.Abs(ev[1][0][0]), 4));
Assert.AreEqual(expEV11, Math.Round(Math.Abs(ev[1][1][1]), 4));
Assert.AreEqual(expEV22, Math.Round(Math.Abs(ev[1][2][2]), 4));
}
Стоит отметить, что собственные векторы могут менять направление от итерации к итерации, что будет видно по изменению знаков их координат, но, очевидно, это несущественно.
Реализация метода главных компонент Теперь все готово для реализации темы статьи.
Скрытым параметром модели (класса) будет определенное подмножество собственных векторов ковариационной матрицы из исходных данных: private IList<double[]> _eigenVectors = null;
Конструктор принимает на вход массив данных и размерность, до которой должно быть уменьшено пространство признаков, а также параметры для QR-декомпозиции.
Внутренне вычисляется ковариационная матрица и берутся первые несколько собственных векторов.
В общем, есть способ выбрать оптимальное количество собственных векторов для желаемого параметра потери информации, т. е.
до какого измерения можно уменьшить пространство, не потеряв более фиксированного процента информации, но я опускаю этот шаг; послушать его можно в лекции Эндрю Нга на сайте курса.
internal DimensionalityReductionPCA(IList<double[]> dataSet, double accuracyQR, int maxIterationQR, int componentsNumber)
{
double[][] cov = BasicStatFunctions.CovarianceMatrixOfData(dataSet);
IList<double[][]> eigen = LinearAlgebra.EigenVectorValuesExtractionQRIterative(cov, accuracyQR, maxIterationQR);
IList<double[]> eigenVectors = LinearAlgebra.DecomposeMatrixToColumnVectors(eigen[0]);
if (componentsNumber > eigenVectors.Count)
{
throw new ArgumentException("componentsNumber > eigenVectors.Count");
}
_eigenVectors = new List<double[]>();
for (int i = 0; i < componentsNumber; i++)
{
_eigenVectors.Add(eigenVectors[i]);
}
}
Затем реализуем прямое и обратное преобразование по формулам из начала статьи.
public double[] Transform(double[] dataItem)
{
if (_eigenVectors[0].
Length != dataItem.Length) { throw new ArgumentException("_eigenVectors[0].
Length != dataItem.Length"); } double[] res = new double[_eigenVectors.Count]; for (int i = 0; i < _eigenVectors.Count; i++) { res[i] = 0; for (int j = 0; j < dataItem.Length; j++) { res[i] += _eigenVectors[i][j]*dataItem[j]; } } return res; } public double[] Reconstruct(double[] transformedDataItem) { if (_eigenVectors.Count != transformedDataItem.Length) { throw new ArgumentException("_eigenVectors.Count != transformedDataItem.Length"); } double[] res = new double[_eigenVectors[0].
Length];
for (int i = 0; i < res.Length; i++)
{
res[i] = 0;
for (int j = 0; j < _eigenVectors.Count; j++)
{
res[i] += _eigenVectors[j][i]*transformedDataItem[j];
}
}
return res;
}
Тестирование
Для тестирования придумаем небольшой массив данных и, проверив значения на Matlab (используя код из нашего домашнего задания PCA =), напишем класс для тестирования: [TestFixture(Description = "Test of DimensionalityReductionPCA")]
public class DimensionalityReductionPCATest
{
private IList<double[]> _data = null;
private IDataTransformation<double[]> _transformation = null;
private double[] _v = null;
[SetUp]
public void SetUp()
{
_v = new double[] { 1, 0, 3 };
_data = new List<double[]>()
{
new double[] {1, 2, 23},
new double[] {-3, 17, 5},
new double[] {13, -6, 7},
new double[] {7, 8, -9}
};
_transformation = new DimensionalityReductionPCA(_data, 0.0001, 1000, 2);
}
[Test(Description = "Test of DimensionalityReductionPCA transform")]
public void DimensionalityReductionPCATransformTest()
{
double[] reduced = _transformation.Transform(_v);
double[] expReduced = new double[] {-2.75008, 0.19959};
Assert.IsTrue(Helper.AreEqualVectors(expReduced, reduced, 0.001));
double[] reconstructed = _transformation.Reconstruct(reduced);
double[] expReconstructed = new double[] {-0.21218, -0.87852, 2.60499};
Assert.IsTrue(Helper.AreEqualVectors(expReconstructed, reconstructed, 0.001));
}
Ссылки
- курс на машинное обучение
- статья, в которой описывается итерационный QR-метод
- куча ссылок на Википедию в тексте статьи
NET #машинное обучение #Машинное обучение #.
NET #Интеллектуальный анализ данных #Алгоритмы

-
Синхронизировать Iphone С Google
19 Oct, 24 -
Радио-У №20
19 Oct, 24


