Во многих задачах возникает необходимость использования генератора псевдослучайных чисел.
Итак, у нас есть такая потребность.
В общем, стояла задача создать вычислительную платформу на базе блока РБ8В7 , который должен был использоваться в качестве ускорителя для расчетов конкретной научной задачи.
Скажу несколько слов об этой научной проблеме: необходимо было рассчитывать динамику биологических микротрубочек на временах порядка минуты.
Расчеты представляли собой расчеты с использованием молекулярно-механической модели микротрубочки, разработанной в научной группе.
Планировалось, что на основе полученных результатов вычислений можно будет сделать вывод о механизмах динамической нестабильности микротрубочек.
Необходимость использования ускорителя была связана с тем, что минута эквивалентна достаточно большому количеству вычислительных шагов (~10^12) и, как следствие, большому количеству времени, затраченному на расчеты.
Итак, возвращаясь к теме статьи, в нашем случае генераторы псевдослучайных чисел понадобились для учета теплового движения молекул упомянутых микротрубочек.
Использована базовая архитектура проекта.
архитектура, поддерживающая передачу DMA .
В качестве компонента этой вычислительной платформы необходимо было реализовать IP-ядро, которое было бы способно генерировать новое псевдослучайное нормально распределенное число с плавающей запятой каждый такт и занимало бы как можно меньше ресурсов на ПЛИС.
Подробнее Последнее требование было связано с тем, что, во-первых, помимо этого IP-ядра на ПЛИС должны были присутствовать и другие вычислительные модули + интерфейсная часть, а во-вторых, вычисления в задаче производились над числами с плавающей запятой типа float. типа, которые в случае с ПЛИС отнимают довольно много ресурсов, и в-третьих, на ПЛИС должно было быть несколько ядер.
Требование генерировать случайное число каждый такт определялось архитектурой конечного вычислительного модуля, который, собственно, и использовал эти случайные числа.
Архитектура представляла собой конвейер и, соответственно, требовала новых случайных чисел каждый такт. Хочу отметить, что в итоге нам это удалось, но путь к решению этой проблемы не обошёлся без неверных шагов и ошибок, о которых я также хочу написать ниже.
Надеюсь, эта статья будет полезна.
Для решения этой проблемы мы использовали транслятор языка высокого уровня в код RTL. Для реализации сложной вычислительной задачи такой подход позволяет получить результаты гораздо быстрее (а зачастую и лучше), чем при использовании голого RTL. Мы использовали программу Вивадо ЗОЖ версия 2014.4, которая преобразует код C/C++ с помощью специальных директив в код RTL. Примеры директив можно посмотреть здесь .
Учитывая упомянутые требования к разрабатываемому решению и то, что генератор должен включать в себя несколько этапов вычислений, наиболее подходящей архитектурой является конвейерная.
Подробнее о реализации конвейера на FPGA можно прочитать здесь.
Здесь .
Хотелось бы отметить, что основными характеристиками вычислительного конвейера являются интервал инициализации и задержка.
Интервал инициализации — это количество тактов, необходимое для выполнения этапа конвейера (максимальное среди всех этапов).
Задержка — это количество тактов, прошедших с момента поступления данных на вход конвейера до момента выдачи конвейером результата.
В данном случае нас не очень интересует задержка, так как она ничтожна по сравнению с ожидаемым общим временем работы конвейера, но к интервалу инициализации следует относиться очень внимательно, так как он фактически характеризует, как часто конвейер способен получать данные.
в качестве входных данных и, соответственно, как часто он способен давать новый результат. Первоначально было решено использовать следующий подход:
- Регистры сдвига с линейной обратной связью для получения независимых целых чисел из равномерно распределенных случайных чисел.
Вначале каждый из них инициируется с использованием своего «начального» номера, т. н.
семя.
- центральная предельная теорема, позволяющая утверждать, что сумма большого числа независимых случайных величин имеет распределение, близкое к нормальному.
В нашем случае суммируются 12 чисел.
Среди преимуществ такого подхода стоит отметить то, что этот обычный генератор чисел реализуется в конечную схему очень просто и действительно не занимает много времени.#pragma HLS PIPELINE unsigned lsb = lfsr & 1; lfsr >>= 1; if (lsb == 1) lfsr ^= 0x80400002; return lfsr;
Главный недостаток этого подхода в том, что в нашем случае он неверен.
=) Действительно, последовательные значения, которые выдаёт генератор, коррелируют. Это можно наглядно продемонстрировать, построив автокорреляционную функцию (см.
рисунок) или построив зависимость x[i+k] от x[i], где k = 1,2,3. Автокорреляционная функция 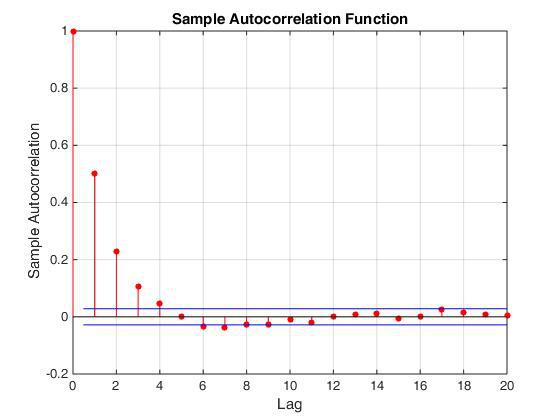
Эта ошибка привела к интересным эффектам в динамике микротрубочек, движение которых моделировалось с помощью этого генератора.

Итак, алгоритм генерации равномерно распределенных целых чисел необходимо было изменить.
Выбор пал на Мерсенн Вихрь .
Убедиться, что значения сгенерированных чисел в этом алгоритме не коррелируют друг с другом, можно, посмотрев на автокорреляционную функцию полученной последовательности чисел.
Однако реализация этого алгоритма требует больше ресурсов, так как он работает с полем чисел размером 612, а не с одним числом, как в предыдущем случае (см.
код находится в свободном доступе ).
автокорреляционная функция 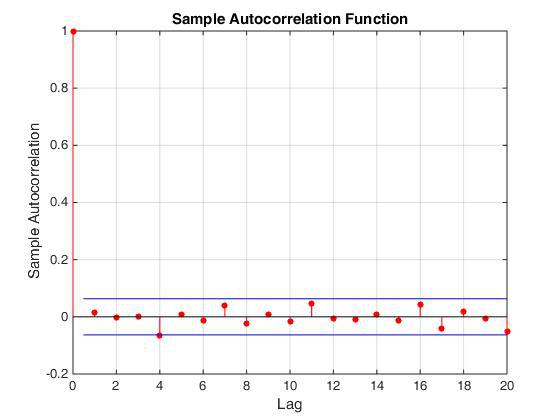
Сразу оговорюсь, что я подразумеваю под словами «процедура занимает n тактов (шагов)».
Это означает, что данная процедура при трансляции в RTL будет выполняться за n тактовых импульсов.
Например, если на следующем шаге конвейера нам необходимо прочитать два слова из однопортовой оперативной памяти, то эта операция выполнится за два такта, так как порт только один, то есть память может обеспечить только один запрос на запись или чтение за такт. Чтобы оптимально перевести этот алгоритм в RTL, код необходимо было переработать.
Во-первых, в исходной реализации внутри генератора происходит следующее: при запросе нового случайного числа либо на выход отправляется следующий элемент матрицы, либо по достижении конца матрицы происходит процедура обновления элементов матрицы.
.
Процедура обновления включает в себя различные побитовые операции с использованием элементов массива.
Процедура занимает не менее 612 шагов по мере обновления значения каждого элемента.
Затем на выход подается нулевой элемент матрицы.
Таким образом, процедура будет выполнять разное количество шагов для разных вызовов данной функции.
Такая функция не может быть конвейерной.
Вариант 0 unsigned long y;
if (mti >= N) { /* generate N words at one time */
int kk;
if (mti == N+1) /* if sgenrand() has not been called, */
sgenrand(4357); /* a default initial seed is used */
for (kk=0;kk<N-M;kk++) {
y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1];
}
for (;kk<N-1;kk++) {
y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1];
}
y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1];
mti = 0;
}
y = mt[mti++];
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680UL;
y ^= (y << 15) & 0xefc60000UL;
y ^= (y >> 18);
return ( (double)y * 2.3283064370807974e-10 ); /* reals */
/* return y; */ /* for integer generation */
Давайте изменим эту процедуру: теперь за один вызов функции обновляется предыдущий элемент массива и возвращается текущий элемент. Теперь эта процедура всегда занимает одинаковое количество циклов.
При этом результат в обеих реализациях один и тот же: при обходе матрицы она уже будет заполнена обновленными значениями и можно просто вернуться к нулевому элементу массива.
Теперь эту процедуру действительно можно передать.
Опция 1 #pragma HLS PIPELINE
#pragma HLS INLINE
float y;
unsigned long mt_temp,reg1;
unsigned long
Теги: #vhdl #vhdl #vhdl #vhdl #xilinx #xilinx #vivado #C++ #Высокая производительность #Алгоритмы

-
Барбадос
19 Oct, 24 -
Linuxpc: Следующий Рабочий Стол Linux
19 Oct, 24 -
Системы Управления В Free-To-Play
19 Oct, 24 -
Лента - "Маджонг"
19 Oct, 24 -
Введение В Контейнерный Сервис Amazon Ec2
19 Oct, 24 -
Конкурс Разработчиков Nokia Asha
19 Oct, 24


