Всем привет! Заказчики как-то спрашивали меня, есть ли у меня в проектах целочисленное БПФ, на что я всегда отвечал, что это уже сделано другими в виде готовых, пусть и кривых, но бесплатных IP-ядер (Altera/Xilinx) — берите.
и используйте его.
Однако эти ядра не оптимально , имеют набор «особенностей» и требуют дальнейшей доработки.
В связи с этим, отправившись в очередной плановый отпуск, который мне не хотелось проводить бездарно, я занялся реализацией настраиваемого целочисленного ядра БПФ.
CDPV (процесс отладки ошибок переполнения данных)
В этой статье я хочу рассказать вам, какими способами и средствами реализуются математические операции при вычислении быстрого преобразования Фурье в целочисленном формате на современных микросхемах FPGA. Основой любого БПФ является узел, называемый «бабочка».
Бабочка осуществляет математические операции – сложение, умножение и вычитание.
Именно о реализации «бабочки» и ее завершенных узлах пойдет речь в первую очередь.
За основу взяты современные семейства ПЛИС от Xilinx — это серии Ultrascale и Ultrascale+, а также затронуты более старые серии 6- (Virtex) и 7- (Artix, Kintex, Virtex).
Старые серии в современных проектах в 2018 году не представляют интереса.
Цель статьи – раскрыть особенности реализации пользовательских ядер цифровой обработки сигналов на примере БПФ.
Введение
Ни для кого не секрет, что алгоритмы БПФ прочно вошли в жизнь инженеров цифровой обработки сигналов, а потому этот инструмент необходим постоянно.Ведущие производители ПЛИС, такие как Altera/Xilinx, уже имеют гибко настраиваемые ядра FFT/IFFT, но они имеют ряд ограничений и особенностей, в связи с чем мне не раз приходилось использовать собственные разработки.
Итак, на этот раз мне пришлось реализовать БПФ в целочисленном формате, используя схему Radix-2 на FPGA. В в моей прошлой статье я уже делал БПФ в формате с плавающей запятой, и отсюда вы знаете, что реализация БПФ использует алгоритм двойного параллелизма, то есть ядро может обрабатывать две сложные выборки на одной частоте .
Это ключевая функция БПФ, которая отсутствует в стандартных ядрах БПФ Xilinx. Пример: Требуется разработать блок БПФ, непрерывно обрабатывающий входной поток комплексных чисел на частоте 800 МГц.
Ядро Xilinx с этим не справится (реально достижимые тактовые частоты обработки в современных ПЛИС составляют около 300-400 МГц), либо потребуется каким-то образом прореживать входной поток.
Специальное ядро позволяет без предварительного вмешательства синхронизировать две входные выборки на частоте 400 МГц вместо одной на частоте 800 МГц.
Еще одним недостатком ядра Xilinx FFT является неспособность принимать входные потоки в обратном порядке битов.
В связи с этим огромный ресурс памяти кристалла ПЛИС тратится на переупорядочение данных в обычном порядке.
Для задач быстрой свертки сигналов, когда два узла БПФ расположены рядом, это может стать критическим моментом, то есть задача просто не поместится в выбранный кристалл ПЛИС.
Пользовательское ядро БПФ позволяет получать входные данные в нормальном порядке и выводить их в обратном побитовом порядке, тогда как ядро обратного БПФ, наоборот, принимает данные в обратном побитовом порядке и выводит их в нормальном порядке.
Эдля перестановки данных сохранено два буфера!!! Поскольку большая часть материала в этой статье может пересекаться с предыдущим Я решил сосредоточиться на освещении темы математических операций в целочисленном формате на ПЛИС для реализации БПФ.
Параметры ядра БПФ
- НФФТ – количество бабочек (длина БПФ),
- DATA_WIDTH – разрядность входных данных (4-32),
- TWDL_WIDTH – разрядность поворотных коэффициентов (8-27).
- РЯД – указывает семейство ПЛИС, в котором реализовано БПФ («НОВОЕ» – Ultrascale, «СТАРОЕ» – серия ПЛИС Xilinx 6/7).

Как и любое другое звено цепи, БПФ имеет порты управляющего ввода — тактовый и сброс, а также порты ввода и вывода данных.
Кроме того, ядро использует сигнал USE_FLY, который позволяет динамически отключать бабочки БПФ для отладки процессов или возможности просмотра исходного входного потока.
В таблице ниже показано количество потребляемых ресурсов FPGA в зависимости от длины FFT NFFT для DATA_WIDTH = 16 и двух бит TWDL_WIDTH = 16 и 24 бит. 
Ядро при NFFT=64К стабильно работает на частоте обработки ЧАСТОТА = 375 МГц на чипе Kintex-7 (410T).
Структура проекта
Схематический граф узла БПФ показан на следующем рисунке: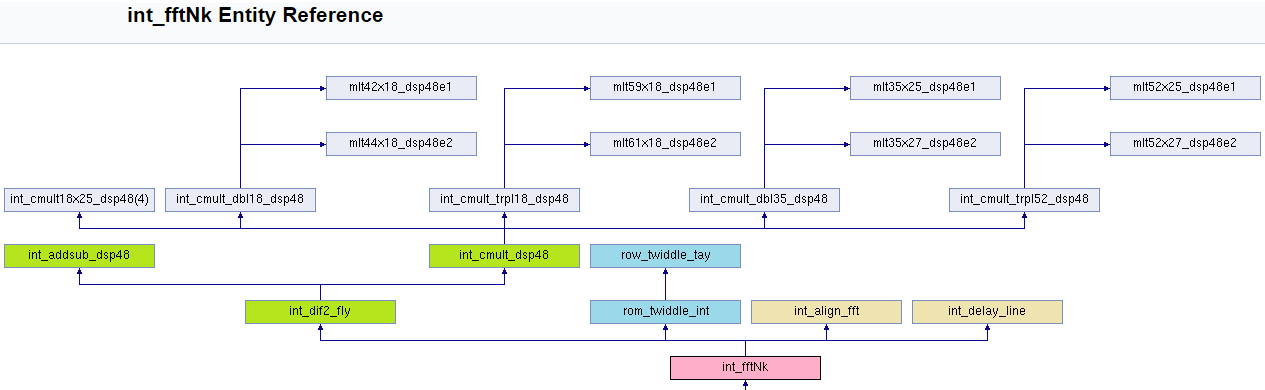
Чтобы было легче понять особенности тех или иных компонентов, приведу список файлов проекта и их краткое описание в иерархическом порядке:
- Ядра БПФ:
- int_fftNk – Узел БПФ, схема Radix-2, частотная децимация (DIF), входной поток – обычный, выходной – побитовый.
- int_ifftNk – узел ОБПФ, схема Radix-2, прореживание времени (DIT), входной поток – побитовый, выходной – обычный.
- int_fftNk – Узел БПФ, схема Radix-2, частотная децимация (DIF), входной поток – обычный, выходной – побитовый.
- Бабочки:
- int_dif2_fly – Бабочка Radix-2, децимация частоты,
- int_dit2_fly – Бабочка Radix-2, прореживание времени,
- Комплексные множители:
- int_cmult_dsp48 – общий настраиваемый множитель, включает в себя:
- int_cmult18x25_dsp48 – множитель для небольших битов данных и коэффициентов поворота,
- int_cmult_dbl18_dsp48 — удвоенный множитель, поворачивающий множители до 18 бит,
- int_cmult_dbl35_dsp48 — удвоенный множитель, поворачивающий множители до 25* бит,
- int_cmult_trpl18_dsp48 — тройной умножитель, поворачивающий множители до 18 бит,
- int_cmult_trpl52_dsp48 — тройной умножитель, поворачивающий множители до 25* бит,
- Множители:
- mlt42x18_dsp48e1 — умножитель с шириной операндов до 42 и 18 бит на базе DSP48E1,
- mlt59x18_dsp48e1 – умножитель с шириной операндов до 59 и 18 бит на базе DSP48E1,
- mlt35x25_dsp48e1 – умножитель с шириной операндов до 35 и 25 бит на базе DSP48E1,
- mlt52x25_dsp48e1 – умножитель с шириной операндов до 52 и 25 бит на базе DSP48E1,
- mlt44x18_dsp48e2 — умножитель с шириной операндов до 44 и 18 бит на базе DSP48E2,
- mlt61x18_dsp48e2 — умножитель с шириной операндов до 61 и 18 бит на базе DSP48E2,
- mlt35x27_dsp48e2 — умножитель с шириной операндов до 35 и 27 бит на базе DSP48E2,
- mlt52x27_dsp48e2 – умножитель с шириной операндов до 52 и 27 бит на базе DSP48E2.
- Сумматор:
- int_addsub_dsp48 – универсальный сумматор, ширина операнда до 96 бит.
- Линии задержки:
- int_delay_line – базовая задержка, обеспечивает перетасовку данных между бабочками,
- int_align_fft – выравнивание входных данных и коэффициентов поворота на входе бабочки БПФ,
- int_align_fft – выравнивание входных данных и коэффициентов поворота на входе ОБПФ-бабочка,
- Вращающиеся множители:
- rom_twiddle_int — генератор поворотных множителей, с определенной длины БПФ вычисляет коэффициенты на основе ячеек DSP ПЛИС,
- row_twiddle_tay – генератор поворотных коэффициентов с использованием ряда Тейлора (NFFT > 2K)**.
- Буфер данных:
- inbuf_half_path – входной буфер, принимает поток в обычном режиме и выдает две последовательности отсчетов, сдвинутых на половину длины БПФ***,
- outbuf_half_path – выходной буфер, собирает две последовательности и выдаёт одну непрерывную, равную длине БПФ,
- iobuf_flow_int2 – буфер работает в двух режимах: принимает поток в режиме Interleave-2 и выдает две последовательности, сдвинутые на половину длины БПФ.
Или наоборот, в зависимости от опции «БИТРЕВ».
- int_bitrev_ord – простой преобразователь данных из естественного порядка в обратный порядок битов.
Ввиду того, что для БПФ важнее ресурс памяти, можно смело жертвовать вычислительными единицами ради памяти.
*** - входной буфер и линии задержки - вносят существенный вклад в объем занимаемых ресурсов памяти ПЛИС.
«Бабочка» Любой, кто хоть раз сталкивался с алгоритмом быстрого преобразования Фурье, знает, что в основе этого алгоритма лежит элементарная операция – «бабочка».
Он преобразует входной поток, умножая входные данные на коэффициенты вращения.
Для БПФ существуют две классические схемы преобразования — прореживание по частоте (DIF, decimation-in- Frequency) и прореживание по времени (DIT, decimation-in-time).
Алгоритм DIT характеризуется разделением входной последовательности на две последовательности половинной длительности, а алгоритм DIF характеризуется разделением входной последовательности на две последовательности четных и нечетных выборок продолжительности NFFT. Кроме того, эти алгоритмы различаются математическими операциями для операции «бабочка».
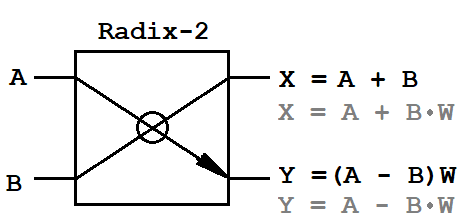
А, Б – входные пары сложных выборок, Х, Ю – выходные пары сложных выборок, Вт являются сложными поворотными факторами.
Поскольку входные данные представляют собой комплексные величины, для бабочки требуется один комплексный умножитель (4 операции умножения и 2 операции сложения) и два комплексных сумматора (4 операции сложения).
Это вся математическая основа, которую необходимо реализовать на ПЛИС.
Множитель
Следует отметить, что все математические операции над ПЛИС часто выполняются в коде с дополнением до 2. Умножитель на ПЛИС может быть реализован двумя способами – на логике, с помощью триггеров и LUT, или на специальных вычислительных блоках DSP48, которые уже давно прочно вошли во все современные ПЛИС.На логических блоках умножение реализовано с помощью алгоритма Бута или его модификаций, занимает приличное количество логических ресурсов и не всегда удовлетворяет временным ограничениям на высоких частотах обработки данных.
В связи с этим умножители FPGA в современных проектах практически всегда проектируются на базе узлов DSP48 и лишь изредка на логике.
Узел DSP48 представляет собой сложную законченную ячейку, реализующую математические и логические функции.
Основные операции: умножение, сложение, вычитание, накопление, счетчик, логические операции (XOR, NAND, AND, OR, NOR), возведение в квадрат, сравнение чисел, сдвиг и т. д. На следующем рисунке показана ячейка DSP48E2 для семейства Xilinx Ultrascale+ FPGA. 
Просто настроив входные порты, вычислив операции в узлах и установив задержки внутри узла, вы можете создать высокоскоростную обработчик математических данных.
Отметим, что все топовые производители ПЛИС имеют в среде проектирования стандартные и бесплатные IP-ядра для расчета математических функций на базе узла DSP48. Они позволяют рассчитывать примитивные математические функции и задавать различные задержки на входе и выходе узла.
В Xilinx имеется «множитель» IP-Core (версия 12.0, 2018 г.
), который позволяет настроить множитель для любой ширины входных данных от 2 до 64 бит. Кроме того, вы можете указать, как реализован множитель — с помощью логических ресурсов или встроенных примитивов DSP48. Оцените, сколько логики «съедает» умножитель с шириной входных данных на портах A и B = 64 бита.
Если вы используете узлы DSP48, то их потребуется всего 16. 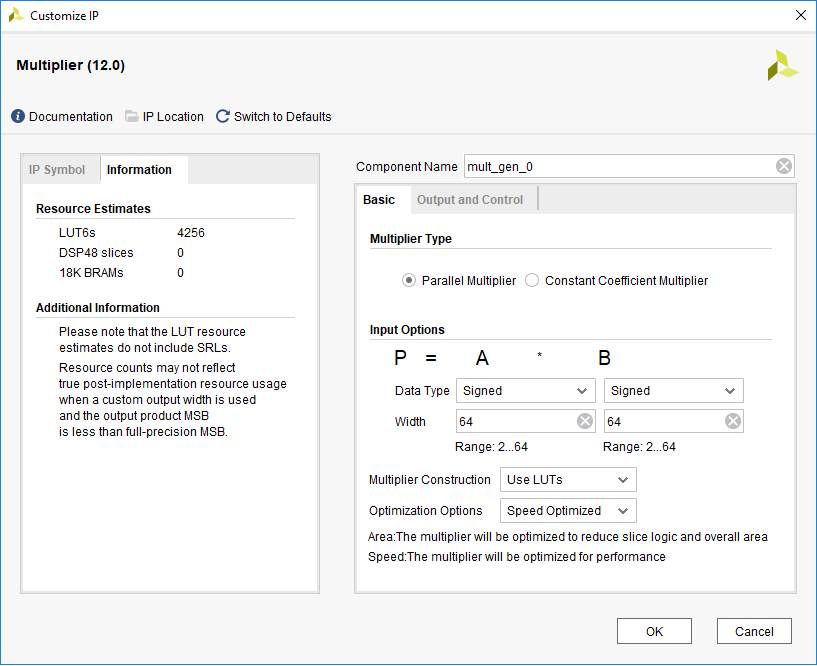
Основным ограничением, налагаемым на ячейки DSP48, является ширина входных данных.
В узле DSP48E1, который является базовой ячейкой ПЛИС Xilinx 6 и 7 серий, ширина входных портов умножения равна: «А» — 25 бит, «В» — 18 бит, Следовательно, результат умножения представляет собой 43-битное число.
Для семейства ПЛИС Xilinx Ultrascale и Ultrascale+ узел претерпел ряд изменений, в частности, разрядность первого порта увеличилась на два бита: «А» — 27 бит, «В» — 18 бит. Кроме того, сам узел называется DSP48E2. Чтобы не быть привязанными к конкретному семейству ПЛИС и кристаллу, обеспечить «чистоту исходного кода» и учесть все возможные разрядности входных данных, было решено спроектировать собственный набор множителей.
Это позволит максимально эффективно реализовать сложные умножители для бабочек БПФ, а именно умножители и сумматор-вычитатель на базе блоков DSP48. Первый вход множителя — входные данные, второй вход множителя — коэффициенты поворота (гармонический сигнал из памяти).
Набор множителей реализован с помощью встроенной библиотеки UNISIM, из которой необходимо подключить примитивы DSP48E1 и DSP48E2 для их дальнейшего использования в проекте.
Набор множителей представлен в таблице.
Необходимо отметить, что:
- Операция умножения чисел приводит к увеличению разрядности произведения как суммы разрядностей операндов.
- Каждый из множителей 25x18 и 27x18 дублируется; по сути, они являются одним компонентом для разных семей.
- Чем выше этап параллелизма операции, тем больше задержка вычислений и тем больше количество потребляемых ресурсов.
- При меньшей разрядности на входе «В» можно реализовать умножители с большей разрядностью на другом входе.
- Основным ограничением увеличения разрядности является порт «B» (настоящий порт примитива DSP48) и внутренний 17-битный сдвиговый регистр.

Дальнейшее увеличение разрядности не представляет интереса в рамках поставленной задачи по причинам, описанным ниже:
Разрядность множителей поворота
Известно, что чем больше разрядность гармонического сигнала, тем точнее представляется число (больше цифр в дробной части).Но ширина порта B < 25 bits due to the fact that for turning multipliers in the FFT nodes, this width is quite sufficient to ensure high-quality multiplication of the input stream with elements of the harmonic signal in the “butterflies” (for any actually achievable FFT lengths on modern FPGAs).
The typical bit size of the turning coefficients in the tasks I implement is 16 bits, 24 – less often, 32 – never.
Разрядность входных выборок
Разрядность данных типовых приемно-регистрирующих устройств (АЦП, ЦАП) невелика — от 8 до 16 бит, реже — 24 или 32 бита.Причем в последнем случае эффективнее использовать формат данных с плавающей запятой по стандарту IEEE-754. С другой стороны, каждый этап «бабочка» в БПФ добавляет один бит данных к выходным выборкам за счет выполняемых математических операций.
Например, для длины NFFT = 1024 используется log2(NFFT) = 10 бабочек.
Следовательно, выходная разрядность будет на десять бит больше входной, WOUT = WIN + 10. В общем виде формула выглядит так: WOUT = WIN + log2(NFFT); Пример: Ширина входного потока WIN = 32 бита, Поворотные мультипликаторы емкостью TWD = 27, Ширина порта «А» из списка реализованных множителей в этой статье не превышает 52 бита.
Это означает, что максимальное количество бабочек БПФ = 52-32 = 20. То есть можно реализовать БПФ длиной до 2^20 = 1М выборок.
(Однако на практике прямым путем это невозможно из-за ограниченности ресурсов даже самых мощных кристаллов ПЛИС, но это уже другая тема и в статье рассматриваться не будет).
Как видите, это одна из основных причин, по которой я не реализовал умножители с входными портами большего размера.
Используемые множители охватывают весь диапазон требуемой разрядности.
входные данные и поворотные коэффициенты для целочисленной задачи БПФ.
Во всех остальных случаях можно воспользоваться расчетом БПФ в формате с плавающей запятой !
Реализация «широкого» мультипликатора
На простом примере умножения двух чисел, которые не умещаются в ширину стандартного узла DSP48, я покажу, как можно реализовать множитель широких данных.На следующем рисунке показана его блок-схема.
Умножитель реализует умножение двух чисел со знаком в коде дополнения до двух; ширина первого операнда X — 42 бита, второго операнда Y — 18 бит. Он содержит два узла DSP48E2. Для выравнивания задержек в верхнем узле используются два регистра.
Это сделано по той причине, что в верхнем сумматоре нужно правильно сложить числа из верхнего и нижнего узла DSP48. Младший сумматор фактически не используется.
На выходе нижнего узла происходит дополнительная задержка произведения для выравнивания выходного номера по времени.
Общая задержка составляет 4 такта.

Работа состоит из двух компонентов:
- Младшая часть: P1 = '0' & X[16:0] * Y[17:0];
- Старшая часть: P2 = X[42:17] * Y[17:0] + (P1 > > 17);
Сумматор
Подобно умножителю, сумматор может быть построен на логических ресурсах с использованием цепи переноса или на блоках DSP48. Для достижения максимальной пропускной способности предпочтителен второй метод. Один примитив DSP48 позволяет реализовать операцию сложения до 48 бит, два узла — до 96 бит. Для реализуемой задачи такой разрядности вполне достаточно.Кроме того, примитив DSP48 имеет специальный режим «SIMD MODE», который распараллеливает встроенное 48-битное АЛУ на несколько операций с разными мелкобитовыми данными.
То есть в режиме «ОДИН» используется полная битовая сетка из 48 бит и двух операндов, а в режиме «ДВА» битовая сетка разбивается на несколько параллельных потоков по 24 бита каждый (4 операнда).
Этот режим с использованием всего одного сумматора позволяет уменьшить количество занимаемых ресурсов кристалла ПЛИС на малых битах входных отсчетов (на первых этапах расчета).
Увеличение разрядности данных
Операция умножение два числа с разрядностью N и M в двоичном дополнительном коде приводят к увеличению разрядности выходного сигнала до П = Н + М .Пример: для умножения трехбитных чисел N = M = 3 максимальное положительное число +3 = (011) 2 , а максимальное отрицательное число равно 4 = (100) 2 .
Самый старший бит отвечает за знак числа.
Следовательно, максимально возможное число при умножении +16 = (010000) 2 , который образуется путем умножения двух максимально отрицательных чисел -4. Ширина выходных данных равна сумме входных битов P = N+M = 6 бит. Операция добавление два числа с разрядностью N и M в двоичном дополнительном коде приводят к увеличению разрядности выходного сигнала на один бит. Пример: сложите два положительных числа, N = M = 3, максимальное положительное число равно 3 = (011) 2 , а максимальное отрицательное число равно 4 = (100) 2 .
Самый старший бит отвечает за знак числа.
Следовательно, максимальное положительное число равно 6 = (0110) 2 , а максимальное отрицательное число равно -8 = (1000) 2 .
Ширина выходных данных увеличивается на один бит.
Учитывая особенности алгоритма
Усечение вверху: Чтобы минимизировать ресурсы FPGA в алгоритме БПФ, при умножении данных в бабочке было решено никогда не использовать максимально возможное отрицательное число для коэффициентов поворота.Данная поправка не оказывает негативного влияния на результат. Например, при использовании 16-битного представления вращающихся множителей минимальное число равно -32768 = 0x8000, а следующее число после него — -32767 = 0x8001. Ошибка при замене максимального отрицательного числа ближайшим соседним значением составит ~0.003% и вполне приемлем для реализации поставленной задачи.
Удалив минимальное число в произведении двух чисел, можно на каждой итерации уменьшить одну неиспользованную старшую цифру.
Пример: данные – 4 = (100) 2 , коэффициент +3 = (011) 2 .
Результат умножения = -12 = (110100) 2 .
Пятый бит можно отбросить, поскольку он дублирует соседний, четвертый — знаковый бит. Усечение разрядности снизу: Очевидно, что при умножении входного сигнала на гармонический эффект в «бабочке» не обязательно расширять разрядность выходного сигнала до следующих бабочек, а требуется округление или усечение.
Коэффициенты поворота представлены в удобном М-битном формате, но на самом деле это обычные синус и косинус, нормированные на единицу.
То есть число 0x8000 = -1, а число 0x7FFF = +1. Следовательно, результат умножения обязательно усекается до исходной разрядности данных (т. е.
M бит из коэффициентов поворота усекаются снизу).
Во всех реализациях БПФ, которые я видел, коэффициенты вращения так или иначе нормируются к 1. Следовательно, из результата умножения необходимо взять биты в следующей сетке [N+M-1-1:M-1].
Старший бит не используется (отнимаем дополнительную 1), младшие биты усекаются.
Сложение/вычитание данных в операциях-бабочках никак не минимизируется и только эта операция способствует увеличение разрядности выходных данных на один бит на каждом этапе расчета .
Отметим, что на первом этапе алгоритма БПФ ДИТ или на последнем этапе алгоритма БПФ DIF данные необходимо умножить на коэффициент поворота с нулевым индексом W0 = {Re, Im} = {1, 0}.
Ввиду того, что умножение на единицу и ноль являются примитивными операциями, их не нужно выполнять.
В этом случае операция комплексного умножения вообще не требуется: действительная и мнимая составляющие подвергаются «вращению» без изменений.
На втором этапе используются два коэффициента: W0 = {Re, Im} = {1, 0} и W1 = {Re, Im} = {0, -1}.
Аналогичным образом операции можно свести к элементарным преобразованиям и использовать мультиплексор для выбора выходной выборки.
Это позволяет существенно сэкономить блоки DSP48 на первых двух бабочках.
Аналогично строится комплексный умножитель – на основе умножителей и сумматора-вычитателя, однако для некоторых вариантов разрядности входных данных не потребуются дополнительные ресурсы, о которых речь пойдет ниже.
Входной буфер, линии задержки и кроссовки аналогичны описанным в предыдущей статье.
Вращающиеся множители стали целочисленными с настраиваемой разрядностью.
В остальном глобальных изменений в конструкции ядра БПФ нет.
Возможности ядра БПФ INT_FFTK
- Полностью конвейерная схема обработки данных.
- Длина преобразования NFFT = 8–512 тыс.
точек.
- Гибкая настройка длины преобразования NFFT.
- Целочисленный формат входных данных, настраиваемая разрядность.
- Целочисленный формат множителей поворота, разрядность настраивается.
- Компактное хранение коэффициентов вращения посредством разложения в ряд Тейлора до первой производной.
- Увеличение разрядности на каждом этапе расчета и на выходе ядра!
- Хранение коэффициентов в течение квартала для экономии ресурсов кристалла.
- БПФ: данные на входе находятся в прямом порядке, на выходе — в двоичном обратном порядке.
- OBPF: входные данные в двоичном обратном порядке, выходные данные в прямом порядке.
- Конвейерная схема обработки с двойным параллелизмом.
Радикс-2.
- Минимальная непрерывная длина пакета данных равна выборкам NFFT*.
- Высокая скорость вычислений и низкое потребление ресурсов.
- Реализация на новейших чипах FPGA (Virtex-6, 7-Series, Ultrascale).
- Частота ядра ~375 МГц на Кинтекс-7
- Язык описания – VHDL.
- Для комбинации FFT+OBPF нет необходимости выполнять операцию обратного битового преобразования.
- Проект с открытым исходным кодом без включения сторонних IP-ядер.
Источник
Исходный код ядра INTFFTK FFT на VHDL (включая базовые операции и набор множителей) и m-скрипты для Matlab/Octave доступно в моем профиле Github .
Заключение
В ходе разработки было спроектировано новое ядро БПФ, обеспечивающее большую производительность по сравнению с аналогами.Комбинация ядер FFT и OBPF не требует преобразования в естественный порядок, а максимальная длина преобразования ограничена только ресурсами FPGA. 2x-параллелизм позволяет обрабатывать двухчастотные входные потоки, чего Xilinx IP-CORE сделать не может. Выходная ширина целочисленного БПФ увеличивается линейно с количеством этапов преобразования.
В прошлой статье я писал о планах на будущее: ядра FFT Radix-4, Radix-8, Ultra-Long FFT на многие миллионы точек, FFT-FP32 (в формате IEEE-754).
Короче говоря, почти все они разрешены, но по тем или иным причинам на данный момент не могут быть обнародованы.
Исключением является алгоритм FFT Radix-8, который я даже не пробовал (он сложный и ленивый).
Еще раз выражаю свою благодарность dsmv2014 , который всегда приветствовал мои авантюрные идеи.
Спасибо за внимание!
ОБНОВЛЕНИЕ 22.08.2018
Добавлена опция в исходные коды МАСШТАБИРОВАННОЕ БПФ/ОБПФ .В каждой бабочке разрядность усекается на 1 бит (усеченный младший бит).
Ширина выходных данных = ширина входных данных.
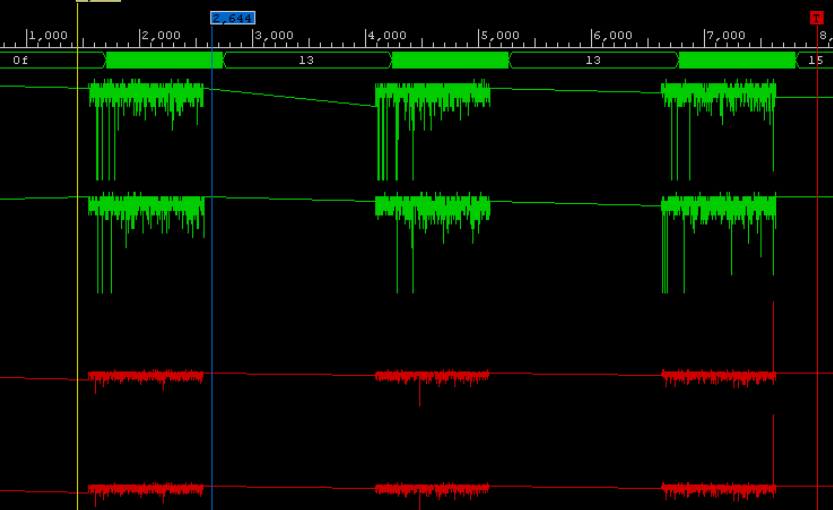
Кроме того, я приведу два графика прохождения реального сигнала через ПЛИС, чтобы показать свойство целочисленности преобразования, то есть: как усечение влияет на результат накопления ошибок на выходе БПФ.
Из теории известно, что в результате преобразования Фурье отношение сигнал/шум ухудшается при усечении входного сигнала относительно варианта без усечения.
Пример: Размах входной амплитуды составляет 6 бит. Сигнал представляет собой синусоиду с частотой 128 отсчетов PF. NFFT = 1024 выборки, DATA_WIDTH = 16, TWDL_WIDTH = 16. Два графика прохождения сигнала через БПФ Рис.
1 Отношение сигнал/шум слабое: 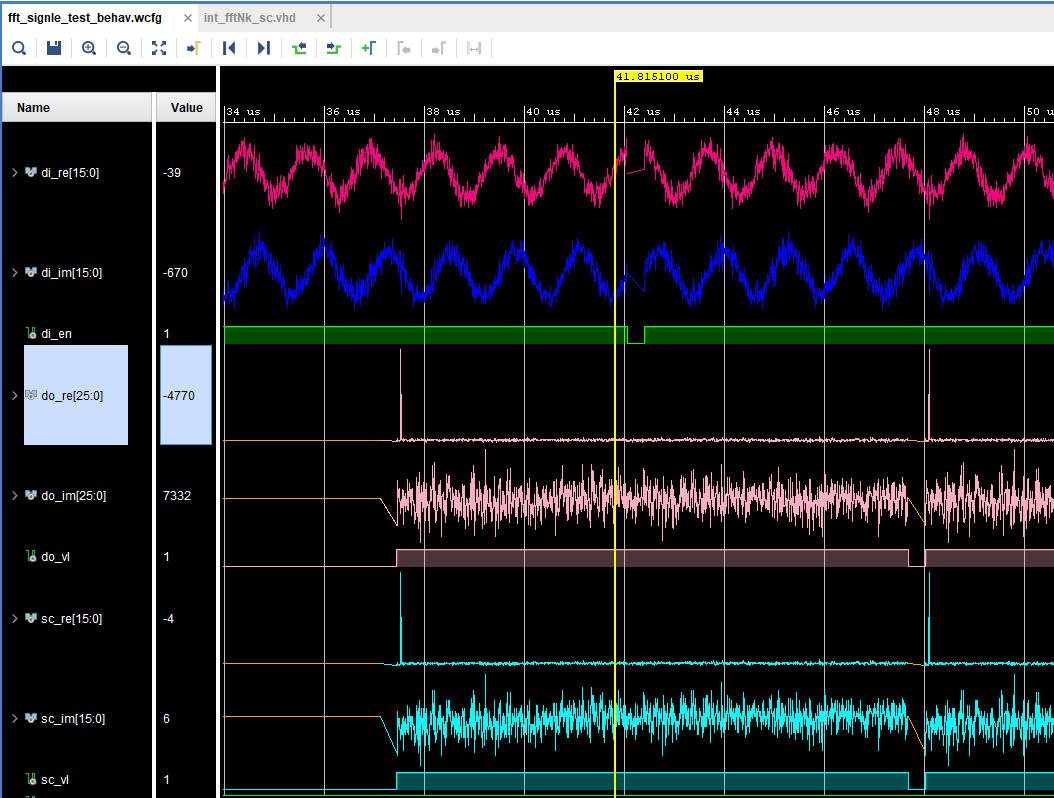
Рис.
2 Отношение сигнал/шум хорошее: 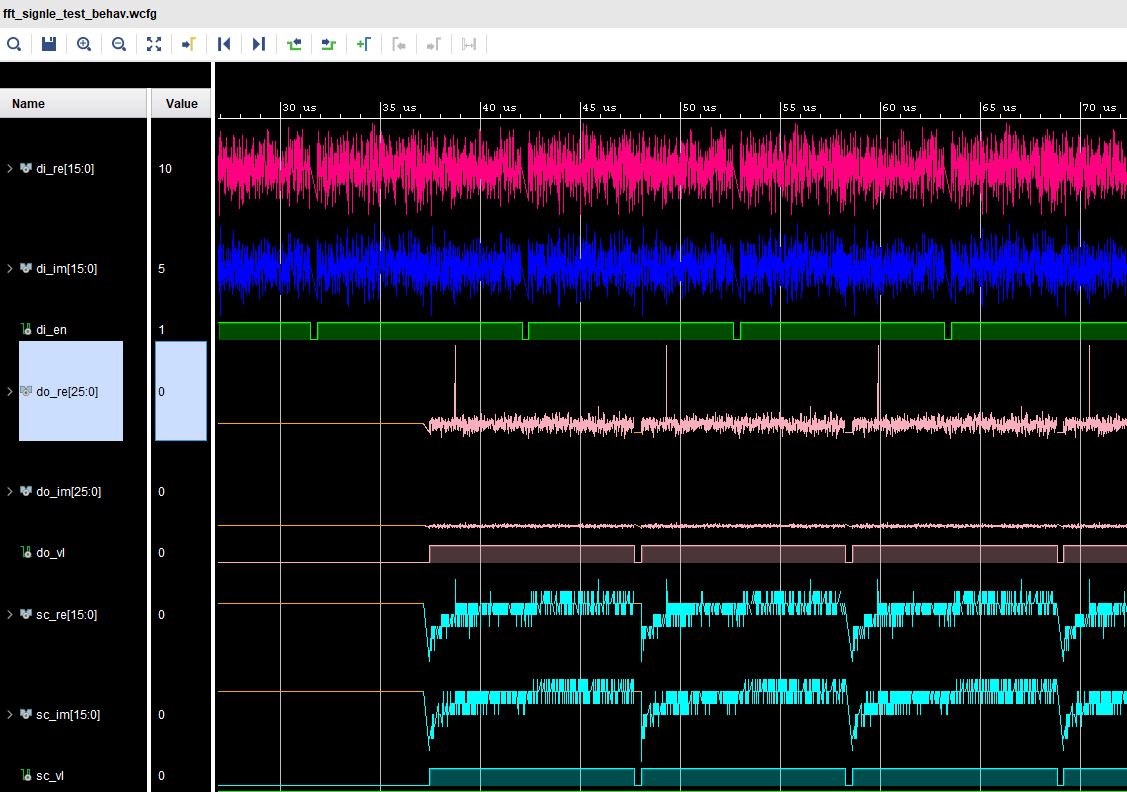
- Розовый — НЕМАСШТАБИРОВАННОЕ БПФ,
- Синий — МАСШТАБИРОВАННОЕ БПФ.

-
Ноутбуки Создают Связь На Подиуме
19 Oct, 24 -
Почему Важно Тестирование Видеоигр
19 Oct, 24 -
Ищем Пневмонию На Рентгене С Помощью Fast.ai
19 Oct, 24 -
Семинар По Symfony Framework
19 Oct, 24


