Аннотация В этой статье я хочу рассказать вам, как можно эффективно распараллелить алгоритм SSSP — поиск кратчайшего пути в графе с помощью графических ускорителей.
Карта с архитектурой GTX Titan будет рассматриваться как графический ускоритель Кеплер .
Введение
В последнее время графические ускорители (GPU) играют все более важную роль в неграфических вычислениях.Необходимость их использования обусловлена их относительно высокой производительностью и меньшей стоимостью.
Как известно, графические процессоры хорошо решают задачи на структурных сетках, где параллелизм так или иначе легко проявляется.
Но есть задачи, требующие больших затрат энергии и использующие неструктурные сетки.
Примером такой проблемы является проблема единственного кратчайшего исходного пути (SSSP) — задача поиска кратчайших путей от заданной вершины ко всем остальным во взвешенном графе.
Для решения этой задачи на ЦП существует как минимум два известных алгоритма: алгоритм Дейсктры и алгоритм Форда-Беллмана.
Существуют также параллельные реализации алгоритмов Дийстры и Форда-Беллмана на графических процессорах.
Вот основные статьи, описывающие решения этой проблемы:
- Ускорение алгоритмов больших графов на графическом процессоре с использованием CUDA, Паван Хариш и П.
Дж.
Нараянан
- Новый подход к решению задачи кратчайшего пути на основе графического процессора, Гектор Ортега-Арранс, Юрий Торрес, Диего Р.
Льянос и Артуро Гонсалес-Эскрибано
Но во всех этих статьях используется один и тот же подход — идея алгоритма Daysktra. Я опишу, как можно использовать идею алгоритма Форда-Беллмана и преимущества архитектуры Кеплера для решения задачи.
Об архитектуре графического процессора и упомянутых алгоритмах уже много написано, поэтому дальше писать об этом в этой статье я не буду.
Также считается, что понятия варпа, cuda-блока, SMX и других базовых вещей, связанных с КУДА знаком читателю.
Описание структуры данных
Давайте кратко рассмотрим структуру хранения неориентированного взвешенного графа, так как к нему будут обращаться и трансформировать его позже.График указан в сжатом формате CSR. Этот формат широко используется для хранения разреженных матриц и графиков.
Для графа с N вершинами и M ребрами необходимы три массива: xadj, adjncy, Weights. Массив xadj имеет размер N+1, два других — 2*M, так как в неориентированном графе для любой пары вершин необходимо хранить прямую и обратную дуги.
Принцип хранения графа следующий.
Весь список соседей вершины I находится в массиве adjncy от индекса xadj[I] до xadj[I+1], не включая его.
Веса каждого ребра из вершины I хранятся с использованием аналогичных индексов.
Для иллюстрации на рисунке слева показан граф из 5 вершин, записанный с использованием матрицы смежности, а справа — в формате CSR. 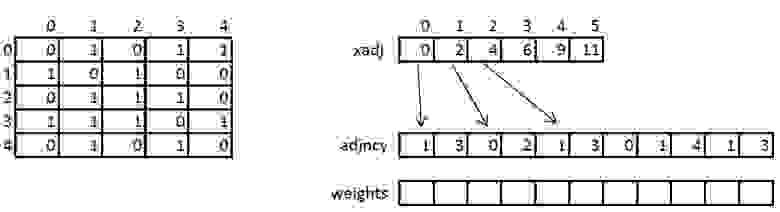
Реализация алгоритма на GPU
Подготовка входных данных
Чтобы увеличить вычислительную нагрузку на один потоковый мультипроцессор (SMX), необходимо преобразовать входные данные.Все преобразования можно разделить на два этапа:
- Расширение формата CSR до формата координат (COO)
- Сортировка формата COO
Тогда их концы будут храниться в массиве adjncy. Таким образом, вместо хранения соседей мы будем хранить дуги.
Пример такого преобразования на графе описан выше: 
На втором этапе необходимо отсортировать полученные ребра так, чтобы каждая пара (U,V) встречалась ровно один раз.
Таким образом, при обработке ребра (U,V) можно сразу обработать ребро (V,U), не перечитывая данные об этом ребре из глобальной памяти графического процессора.
Основное вычислительное ядро
Алгоритм взят за основу для реализации на GPU. Форд-Беллман .Этот алгоритм хорошо подходит для реализации на GPU благодаря тому, что ребра можно просматривать независимо друг от друга, а данные ребер и их веса располагаются подряд, что улучшает пропускную способность памяти GPU:
Теги: #sssp #cuda #GPGPU #nvidia #Intel #kepler #GPGPUint k = blockIdx.x * blockDim.x + threadIdx.x; if(k < maxV) {

-
Касперский Против Sopa
19 Oct, 24 -
Самая Трудная Игра
19 Oct, 24


