Вы можете свободно прочитать первую часть Здесь .
Итак, дорогие друзья, в предыдущей части мы говорили о параллельном переносе, а сегодня займемся ротацией.
Это будет интересно.
Теперь давайте быстренько вспомним основные понятия и двинемся дальше.
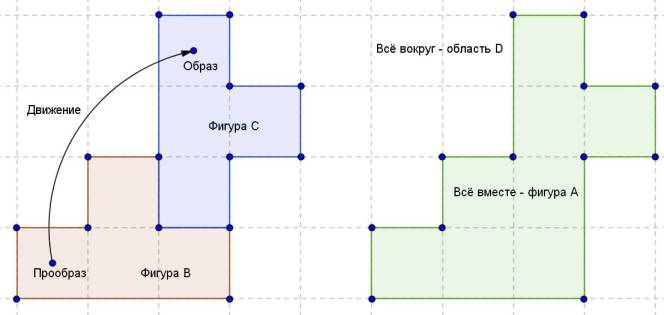
Случай 2: поворот
Вращение, как известно, характеризуется двумя параметрами: точкой, вокруг которой все вращается (центр вращения), и углом, на который происходит вращение.Начнем с поиска возможного центра вращения.
Для начала творчески переработаем терминологию, введенную в первой части.
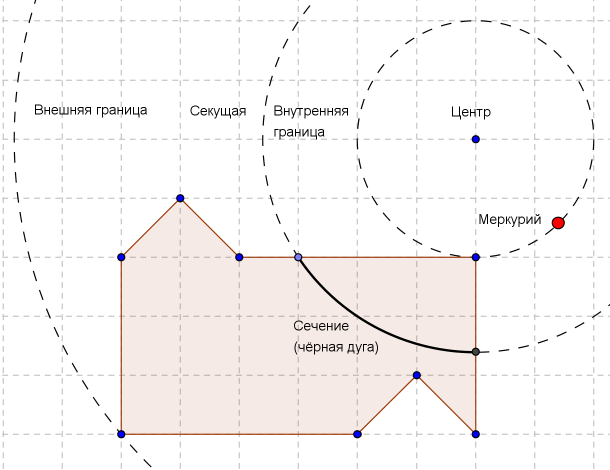
секанс Теперь появятся окружности с центром в центре вращения (простите за тавтологию), имеющие хотя бы одну общую точку с фигурой А.
Разделы — пересечение этих кругов с фигурой.
Границы - окружности, относительно которых фигура за вычетом сечения находится либо целиком внутри, либо целиком снаружи.
В первом случае это будет внешняя граница , В секунду - внутренняя граница .
Заметим, что внутренняя граница существует тогда и только тогда, когда центр вращения находится вне фигуры (если считать фигуру замкнутой, добавил бы дотошный математик).
В этих условиях остаются справедливыми леммы 1 и 2 из первой части, которыми мы свободно воспользуемся.
Случай 2.1: центр вращения вне фигуры
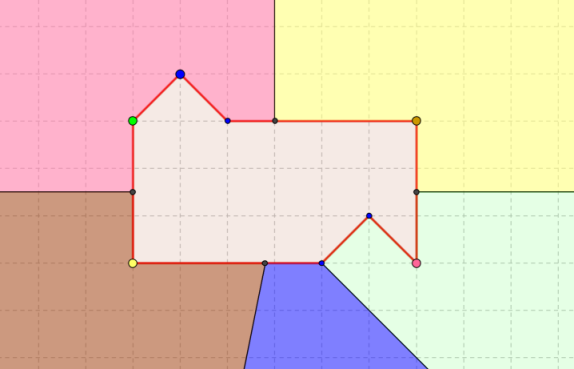
Сейчас я нарисую красивую разноцветную картинку.Каждый цвет представляет собой геометрическое положение точек, для которых, если бы они были центром вращения, дальняя граничная секция состояла бы из одной конкретной вершины фигуры А.
0 (каждая вершина имеет свой цвет, это показано на картинке).
Поскольку граничное сечение, как и любое другое сечение, не может состоять из одной точки (см.
лемму 1), центр вращения может располагаться только на черных линиях между цветными областями.
Если кому-то интересно, откуда у нас берутся черные линии, это медианные перпендикуляры к отрезкам между соответствующими парами вершин.
Потом нарисую еще одну красочную картинку, на этот раз для ближних границ.
Обратите внимание, что ближайшая к центру вращения точка, в отличие от самой дальней, не обязательно должна быть вершиной – она может лежать и на стороне (области, соответствующие сторонам, окрашены в оттенки серого).
Границы между областями, соответствующими стороне и вершине на этой стороне, не подходят для размещения центра вращения (в этом случае ближайший участок границы все равно состоял бы из одной точки), поэтому я нарисовал их пунктиром линия.
Толстая черно-желто-черная граница представляет собой кусок параболы (именно такая форма границы между областью сбоку и областью вверху, Нет принадлежность к этой партии).
Хотелось бы сказать, что желтая полоса посередине параболической дуги – это особенность, но на самом деле это непонятный неустранимый артефакт, возникший на стыке двух изогнутых участков.
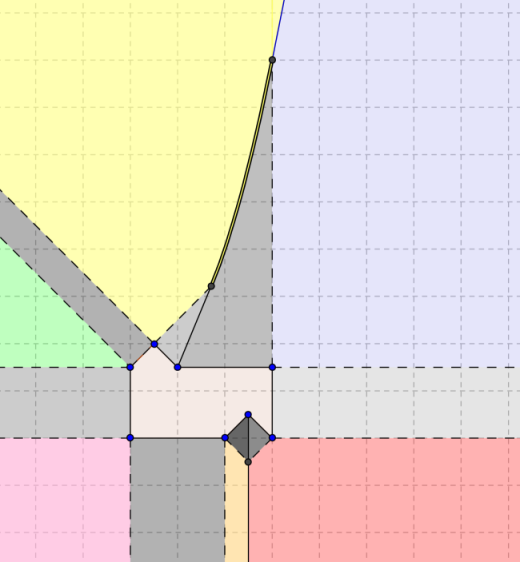
Из этой картинки (все сходства с кислотной атакой случайны и непреднамеренны) видно, что ограничение, наложенное на ближнюю границу, оставляет не так много мест, где мог бы располагаться центр вращения: балка внизу и сложная хрень (поворотный сегмент в дугу параболы, которая затем превращается в балку) вверху.
Теперь остается только наложить картинки друг на друга и посмотреть, какие точки «приемлемы» на обоих.

Легко видеть, что таких точек всего две (я их обозначил O 1 и О 2 ).
Однако могут ли они на самом деле быть центрами вращения, превращающими друг в друга гипотетические равные куски фигуры А? 0 ? Очевидно нет. Тогда дуги между парами точек на ближней и дальней границах имели бы одинаковую угловую меру, поскольку угол поворота не зависит от расстояния до центра.
При этом угловые меры всех четырех дуг (см.
рисунок) различны.
Таким образом, случай центра вне фигуры можно считать закрытым.
Заключение
Если фигура А 0 и можно разрезать на две равные фигуры В и С, то движение, превращающее В в С, не может быть не только параллельным переносом, но и вращением, центр которого находится вне фигуры.Случай вращения с центром внутри фигуры я решил вынести в отдельную статью: из-за незамеченных ранее технических трудностей объем доказательства для этого случая сильно раздулся.
Продолжение следует. Теги: #математика #геометрия #комбинаторная геометрия #ололошечки и бугагашечки #математика

-
Убунту+Линспайр
19 Oct, 24 -
Будущее Winrt Или Going Native 2.0
19 Oct, 24 -
Как Мы Снимали Видео Для Cms
19 Oct, 24 -
Джава. Остановить Задачу
19 Oct, 24 -
Еще Один «Гуглотелефон» Acer A1
19 Oct, 24


