В последнее время задача распознавания символов в прикладных программах не представляет особой сложности — можно использовать множество готовых библиотек оптического распознавания символов, многие из которых доведены практически до совершенства.
Но все же иногда может возникнуть задача разработать собственный алгоритм распознавания без использования сторонних «навороченных» библиотек OCR. Это именно та проблема, которая возникла во время моей работы, и есть несколько причин, по которым лучше не использовать готовые библиотеки: закрытость проекта, с его дальнейшей сертификацией, определенное ограничение на количество строк кода.
и размер подключаемых библиотек, тем более, что по предметной области приходится довольно много распознавать определенный набор символов.
Алгоритм распознавания прост и, конечно, не претендует на звание самого точного, быстрого и эффективного, но со своей небольшой задачей справляется хорошо.
Допустим, у нас есть входные данные в виде сканированных изображений документов в структурированном виде.
Эти документы имеют специальный односимвольный код, расположенный в левом верхнем углу.
Наша задача — распознать этот символ и затем выполнить какие-то действия, например, классифицировать исходный документ по заданным правилам.

Схема алгоритма выглядит следующим образом: 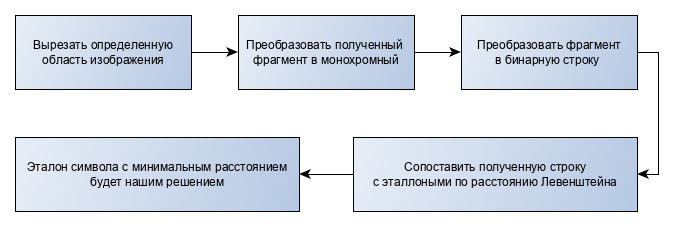
Поскольку мы заранее знаем, где находится наш символ, вырезать определенную область не составит труда.
Чтобы убрать все «неровности» краев символа, преобразуем изображение в монохромное (черно-белое).
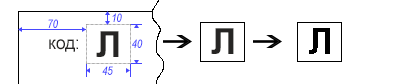
Далее необходимо преобразовать полученный фрагмент «попиксельно» в бинарную строку, то есть строку, где, например, черный пиксель соответствует '*', а белый пиксель соответствует пробелу.short width = 45, height = 40, offsetTop = -10, offsetLeft = -70; BufferedImage image = ImageIO.read(file); BufferedImage symbol = new BufferedImage(width, height, BufferedImage.TYPE_BYTE_BINARY); Graphics2D g = symbol.createGraphics(); g.drawImage(image, offsetLeft, offsetTop, null);
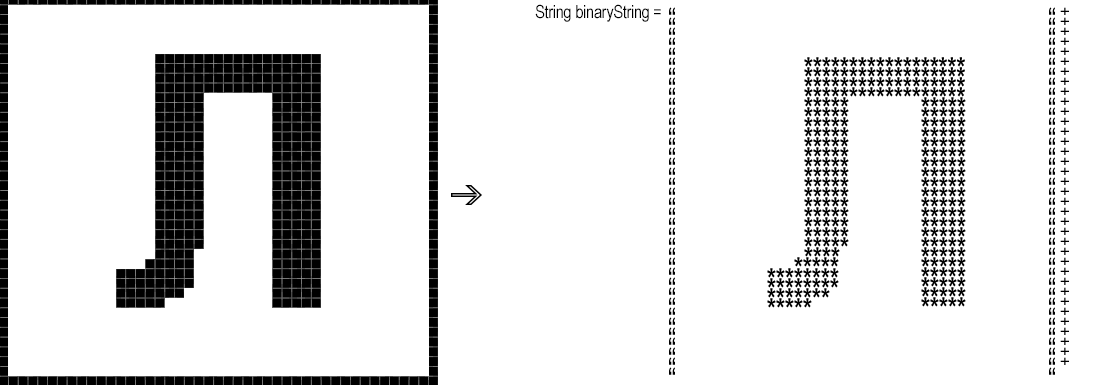
short whiteBg = -1;
StringBuilder binaryString = new StringBuilder();
for (short y = 1; y < height; y++)
for (short x = 1; x < width; x++) {
int rgb = symbol.getRGB(x, y);
binaryString.append(rgb == whiteBg ? " " : "*");
}
Далее необходимо найти минимальное расстояние Левенштейна между полученной строкой и заранее подготовленными эталонными строками (по сути, можно использовать любой метод сравнения строк).
int min = 1000000;
char findSymbol = "";
for (Map.Entry<Character, String> entry : originalMap.entrySet()) {
int levenshtein = levenshtein(binaryString.toString(), entry.getValue());
if (levenshtein < min) {
min = levenshtein;
findSymbol = entry.getKey();
}
}
Функция нахождения расстояния Левенштейна реализована в виде метода по стандартному алгоритму: public static int levenshtein(String targetStr, String sourceStr) {
int m = targetStr.length(), n = sourceStr.length();
int[][] delta = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++)
delta[i][0] = i;
for (int j = 1; j <= n; j++)
delta[0][j] = j;
for (int j = 1; j <= n; j++)
for (int i = 1; i <= m; i++) {
if (targetStr.charAt(i - 1) == sourceStr.charAt(j - 1))
delta[i][j] = delta[i - 1][j - 1];
else
delta[i][j] = Math.min(delta[i - 1][j] + 1,
Math.min(delta[i][j - 1] + 1, delta[i - 1][j - 1] + 1));
}
return delta[m][n];
}
Полученный findSymbol будет нашим распознаваемым символом.
Этот алгоритм можно оптимизировать для повышения производительности и дополнить различными проверками для повышения эффективности распознавания.
Многие показатели зависят от конкретной предметной области решаемой задачи (количество символов, разнообразие шрифтов, качество изображения и т. д.).
Практическим путем выяснилось, что метод качественно справляется даже с такими проблемными вопросами, как «похожесть» символов, например «Л».
<-> «П», «5»<-> "ТАК"<-> «0» Так как, например, расстояние между двоичными строками «L» и «P» всегда будет больше, чем между распознаваемым «L» и эталонной строкой «L», даже с некоторыми «неровностями».
В общем, если вам нужно решить подобную задачу (например, распознавание игральных карт) с рядом ограничений на использование нейронов и других готовых решений, то можно смело брать и модифицировать этот метод. Теги: #программирование #java #дистанция Левенштейна #распознавание символов

-
Автономный Роутер Для 4G Мегафон
19 Oct, 24 -
Intel На Ces 2017: Планы На Год
19 Oct, 24


