В этой статье я описываю простой метод генерации точечного ряда на основе псевдослучайного ряда с малой расходимостью, который демонстрирует улучшенные изотропные свойства синего шума.
Он обеспечивает высокую скорость сходимости с минимальными артефактами сглаживания.
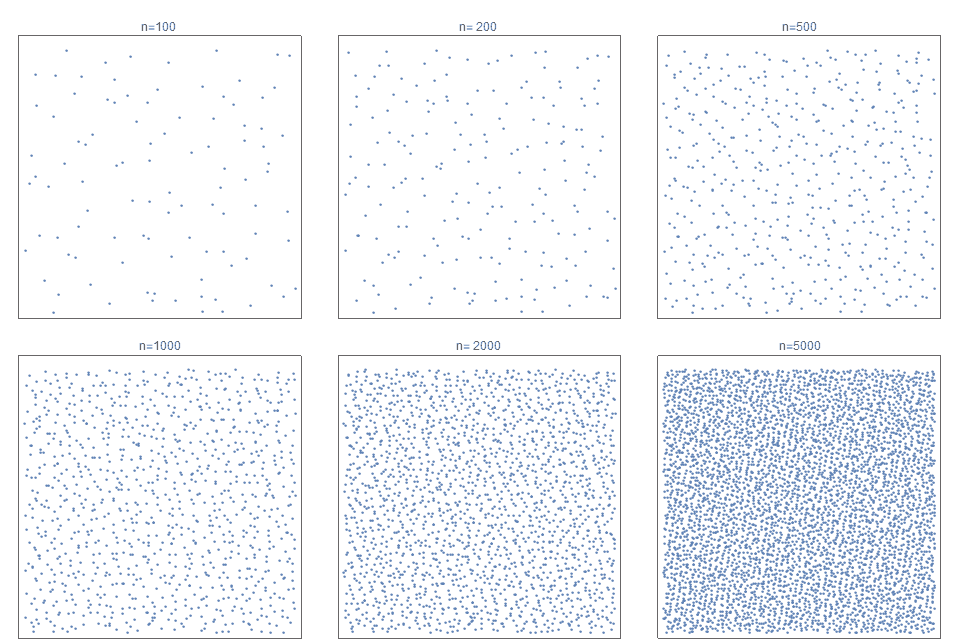
Рисунок 1. Первые 100, 200, 500, 1000, 2000 и 5000 точек выборки из предложенного прогрессивного нестохастического ряда точек (уравнение 11), демонстрирующие почти изотропные характеристики синего шума с быстрой сходимостью QMC и уменьшенными артефактами.
Ряд основан на новой простой псевдослучайной последовательности с низкой дивергенцией.
.
Введение Псевдослучайные ряды с низким расхождением используются для создания распределений, которые менее регулярны, чем сетки, но более регулярны, чем простые случайные распределения (см.
рисунок 2).
Они играют важную роль во многих областях численных вычислений, включая физику, финансы и, в последнее время, компьютерную графику.

Рисунок 2. Сравнение регулярной решетки (слева) с тремя различными псевдослучайными функциями (в центре) и простым случайным распределением (справа).
Обратите внимание, что псевдослучайные распределения кажутся менее регулярными, чем решетка, но не имеют такого количества кластеров и редких точек, как случайное распределение.
Классическая статья о том, как использование псевдослучайной выборки вместо равномерной выборки может улучшить 2D-изображения: Стохастическая выборка в компьютерной графике [ Кук, 1986 год. ].
За последние десятилетия псевдослучайная выборка стала важным инструментом 3D-рендеринга.
Рендереры (и сэмплеры) могут использовать для вычислений как ЦП, так и графический процессор.
Отличным примером их использования в 3D-рендеринге является Сглаженные сэмплеры с низким расхождением для оценщиков Монте-Карло при физически обоснованном рендеринге [ Перье, 2108 г.
].
В этой статье автор рассказывает о задаче 3D-рендеринга (см.
рисунок 3) следующим образом: «Когда вы отображаете 3D-объект на экране компьютера, эта 3D-сцена превращается в 2D-изображение, представляющее собой набор упорядоченных цветных пикселей.
Мы называем рендерингом процесс, целью которого является поиск правильных цветов для этих пикселей.
Это реализуется путем моделирования и интеграции всего освещения.
Мы аппроксимируем уравнение численно, взяв случайные выборки в области интегрирования и аппроксимируя значение интегрируемой функции методами Монте-Карло.
Стохастический сэмплер должен минимизировать дисперсию интегрирования, чтобы сходиться к правильному приближению с использованием как можно меньшего количества выборок.
Существует множество различных сэмплеров, которые можно условно разделить на два семейства: — Синие ушные пробоотборники, которые имеют низкую дисперсию интегрирования, но генерируют неструктурированные наборы точек.
Проблема с этими пробоотборниками заключается в том, что они часто медленно генерируют несколько точек.
- Пробоотборники с низким расхождением, которые минимизируют дисперсию интегрирования и могут очень быстро генерировать и заполнять несколько точек.
Однако при использовании при рендеринге они создают множество структурных артефактов».
Недавно были предприняты попытки объединить преимущества сглаживания джиттерной выборки с высокой скоростью сходимости (низкой дисперсией), характерной для псевдослучайных последовательностей с низкой расходимостью.
].
С этой же целью я ввел новый способ построения бесконечный ряд точек, что чрезвычайно простой , быстрый в вычислительной технике, прогрессивный , в полной мере детерминированный , что демонстрирует быстрая сходимость (низкая дисперсия) с необходимым изотропный спектр синий шум и, следовательно, приводит к минимальные артефакты .
Итак, начнем.


Рисунок 3. 3D-рендеринг (слева).
Процесс выборки часто приводит к появлению нежелательных артефактов псевдонимов (справа).
Источник :[ Перье, 2018 г.
] Краткое содержание
простые флуктуационные (конечные) множества точек флуктуационные псевдослучайные наборы точек колебания (бесконечных) псевдослучайных серий Сравнение сходимости QMC заключение пример кода Простая выборка колебаний Простейшими флуктуационными (возмущенными) множествами точек являются флуктуационные сетки.
В нашем случае пространство выборки разделено на сетку
квадратные площади.
Вместо простого выбора точки в центре каждой ячейки выбирается любая (псевдо)случайная точка внутри каждой ячейки.
Преимуществами выборки сетки джиттера являются простота понимания и реализации, а также чрезвычайная скорость вычислений.
Однако у него есть очевидное ограничение –
должен быть идеальный квадрат.
Хотя прямоугольная типологическая выборка может снизить остроту этого ограничения, так что
было произведением двух соответствующих целых чисел, я опишу другой подход, информативный, очень элегантный и гораздо менее известный.
Представим себе, не ограничивая общности, что пространство выборки представляет собой единичный квадрат.
.
Определим решетку Фибоначчи как решетку
точки, где:
Где
- золотое сечение и
обозначает дробную часть
.
Обратите внимание, что в расчетах этот дробный оператор обычно записывается и реализуется как
(произносится как «мод 1»), и поскольку этот пост в основном нацелен на вычислительные приложения, в дальнейшем мы будем использовать это обозначение.
Стоит отметить, что сетка Фибоначчи — очень элегантный способ размещения любое количество точки в единичном квадрате чрезвычайно регулярным образом.
Например, на рисунке 2а показана стандартная сетка Фибоначчи для N=41 точки.
При использовании джиттерной выборки вместо того, чтобы выбирать центр каждого диска в качестве точки выборки, мы можем просто выбрать точку
внутри каждого
диски (см.
рисунок 4б).
Учитывая, что типичное расстояние между точками равно
,
Где
означает, что для
- этого члена случайная выборка берется из круга с центром в нуле и радиусом
.
Следует отметить, что простой прямой метод равномерной выборки окружности радиуса
заключается в том, чтобы сначала взять две равные выборки
И
, каждый из которых находится в интервале
а затем примените следующее преобразование:
Конечно, вы можете уменьшить степень колебания, просто выбрав меньшее значение.
.

Рисунок 4-1. (а) Каноническая сетка Фибоначчи; (б) Флуктуационная решетка Фибоначчи.
Распределения точек, приближенные радиальные спектральные функции и спектры Фурье этих наборов точек показаны ниже.
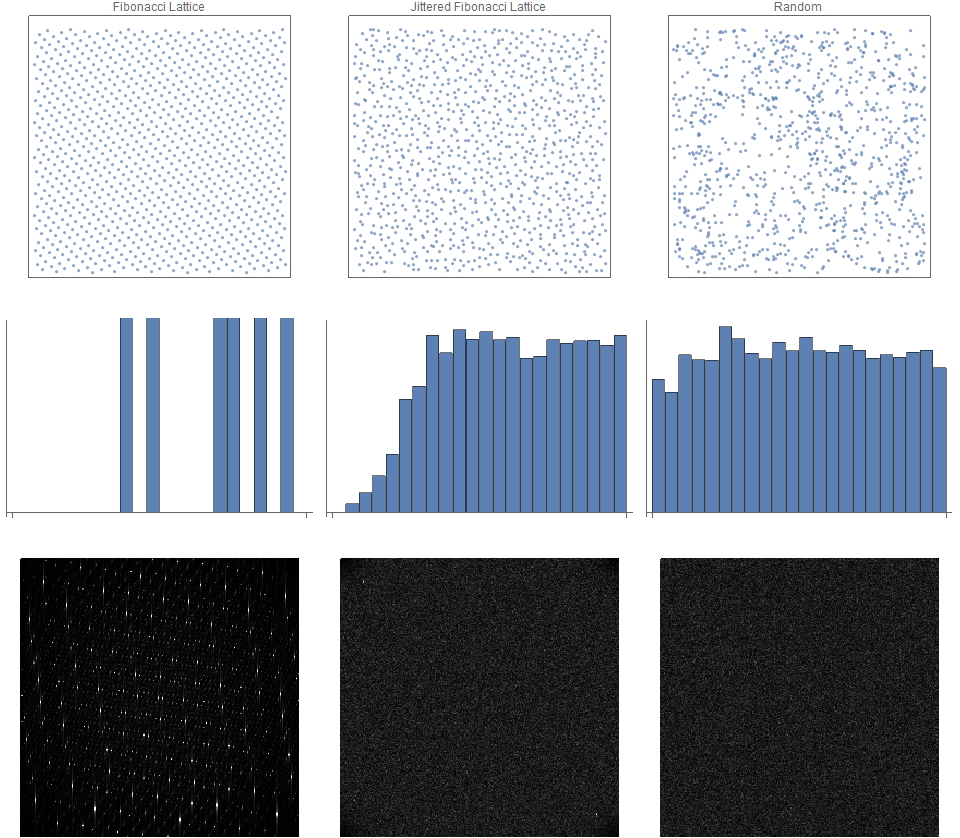
Рисунок 4-2. (а) Каноническая сетка Фибоначчи; (б) решетка флуктуаций Фибоначчи; и (c) случайные выборки.
Если
известно заранее, это простой, но эффективный способ создания изотропного набора точек.
Интересно, что, несмотря на интуитивное ощущение, что между соседними точками существует постоянное расстояние, спектр Фурье для флуктуационного множества точек Фибоначчи не демонстрирует спектр классического синего шума.
Однако эта версия с колебаниями очень хорошо работает во многих приложениях и контекстах!
Однако известно, что существует множество отличных способов создания изотропных наборов точек с учетом априори известных
.
В этом посте мы исследуем менее изученную область прямых построений для открытых/бесконечных изотропных серий точек синего шума, в которых
заранее неизвестно.
Более того, несмотря на чрезвычайно высокую скорость вычислений флуктуационной сетки и флуктуационной решетки Фибоначчи, они обе страдают от построчного упорядочения точек.
Часто предпочтительны методы выборки, при которых последовательные точки не находятся рядом, а скорее «равномерно распределены» по пространству выборки.
Это свойство часто называют «прогрессивной выборкой».
Таким образом, мы исследуем практичность построения прогрессивных изотропных наборов и серий точек синего шума.
Флуктуационные псевдослучайные наборы точек Псевдослучайный ряд с низкой дивергенцией представляет собой (бесконечный) ряд точек, распределенных более равномерно, чем простое случайное распределение, но менее регулярно, чем сетки.
Такие ряды полезны во многих приложениях, таких как интеграция Монте-Карло.
Существует много типов псевдослучайных рядов, включая ряды Вейля/Кронекера, Ван дер Корпута/Холтона, Нидеррайтера и Соболь.
Подробно о них, в том числе и о новом, я рассказал в своем предыдущем посте: Необоснованная эффективность квазислучайных последовательностей .
В этом посте мы рассмотрим только одну из описанных серий – сериал
.
Для сравнения мы также рассмотрим серию Холтона и серию Соболь, поскольку именно они сегодня наиболее часто используются в QMC. Я представлю краткое изложение псевдослучайных рядов с низкой дивергенцией, описанных в этом посте.
: ряд
— это рекурсивный ряд Кронекера/Вейля/Рихтмайера, представленный в моем предыдущем посте.
Он основан на обобщении золотого сечения и поэтому может рассматриваться как естественный способ построения обобщенной сетки Фибоначчи, соединяющей слева направо и сверху вниз.
Оно указано следующим образом:
Стоит отметить, что
, часто называемая пластической константой, имеет набор красивая недвижимость (также см Здесь ).
Серия Холтона :
-мерные ряды Холтона не зависят от
ряды обратного фундамента Ван дер Корпута с частичными швами.
В этом посте мы будем придерживаться традиционной схемы с выбором в качестве баз первых.
простые числа.
Поэтому в этом посте я всегда буду использовать ряд {2,3}-Халтона.
Серия Соболь : Серия «Соболь» обладает множеством превосходных свойств с низкой расходимостью, включая высокую скорость сходимости.
В этом посте построение ряда Соболя (и выбор параметров) будет выполнено с использованием Mathematica версии 10. В документации Mathematica указано, что реализация Соболя «закрытые, проприетарные и полностью оптимизированные генераторы из библиотеки Intel MKL» .
В отличие от конечных наборов точек, строки точек бесконечный .
Ключевое преимущество бесконечной серии состоит в том, что если ошибка после
все еще слишком велико, то вы можете просто выбрать дополнительные точки без необходимости пересчитывать все предыдущие точки.
А преимуществом выборки на основе псевдослучайных рядов является их прогрессивность .
То есть каждая последующая точка находится проксимально далеко от предыдущей, и по мере увеличения количества точек выборки они равномерно заполняют пространство выборки.
На рисунке 5 показаны эти три ряда с малой расходимостью вместе с их преобразованиями Фурье и радиальными спектральными функциями.
Мы можем видеть это: Точки
очень равномерно распределены.
Для многих приложений такое распределение идеально, но для других приложений оно «слишком равномерное».
Все строки с низким неравенством демонстрируют четкие закономерности, которые часто приводят к появлению нежелательных артефактов в изображениях, обработанных с помощью QMC. Спектры Фурье для всех рядов с малой расходимостью состоят из множества пространственно регулярных пиков.
ни один из псевдослучайных наборов точек не является изотропным
радиальная спектральная функция ряда
состоит только из дискретного числа пиков.
радиальные спектральные функции рядов Холтона и Соболя непрерывны, но не гладки.
То есть артефакты рендеринга являются прямым результатом (i) дискретных ярких пиков в спектрах Фурье и/или (ii) дискретных пиков в радиальных спектральных функциях.
Небольшое замечание о том, почему здесь может быть полезен термин «синий шум».
В общем смысле распределение
можно назвать синим шумом, поскольку его низкие (синие) частоты явно подавлены.
Однако он состоит только из дискретных пиков, поэтому, возможно, лучше называть его «дискретным синим шумом» (или вообще не называть его синим шумом).
В более общем контексте «синий шум» требует (i) изотропных спектров Фурье и (ii) радиальной спектральной функции, которая плоская, как белый шум, но с полностью подавленными низкими частотами.
Отличный обзор различных спектров синего шума см.
] Кроме того, некоторые авторы [Perrier, 2018] отмечают, что большинство методов дискретизации диска Пуассона, таких как лучший кандидат Митчелла, не используют строго синий шум, поскольку их спектральные функции малы, но не равны нулю на самых низких частотах.
В этом смысле его лучше называть «приближенным синим шумом».
Также отмечается, что разница между почти нулем и полным нулем может сильно негативно повлиять на скорость сходимости.

Рисунок 5. Наборы точек (n=2000) на основе различных псевдослучайных серий: (i)
, (ii) Холтон; и (iii) Соболь, с (iv) случайным рядом для сравнения.
Спектральные функции ни одного из псевдослучайных рядов не напоминают ни случайный белый шум, ни классический синий шум.
Все они имеют заметные и регулярные дискретные пики, и ни один из них не является изотропным — два классических индикатора того, что они будут вызывать визуальные артефакты.
Нам хотелось бы совместить преимущества сглаживающей флуктуационной выборки с быстрой сходимостью псевдослучайных рядов с низкой расходимостью и, следовательно:
Основная цель этой статьи проста: определить минимальный уровень флуктуации, применяемой к псевдослучайным точкам, такой, чтобы все пики Фурье были подавлены, преобразование стало изотропным, а радиальная спектральная функция для высоких частот стала плоской и однородной - в идеале.Интуитивно понятно, что этот критический уровень колебаний будет тесно связан с типичным расстоянием (деленным напри сохранении низкой частоты подавления
) между соседними точками.
На рисунке 6а показано минимальное расстояние между соседними точками для строк.
, Холтон и Соболь.
Стоит отметить, что ряд
— единственная строка с небольшим расхождением, в которой минимальное расстояние между соседними точками уменьшается со скоростью всего
.
Для серий Холтона и Соболь расстояние падает гораздо быстрее, близко к
.
Аналогично, рисунок 6б показывает, что среднее расстояние между соседними точками
Не меньше
Для
для всех значений
.
Эти показатели дают понять, что колебания будут идеальными.
в радиусе половины этого значения.
Эмпирические тесты подтверждают это.
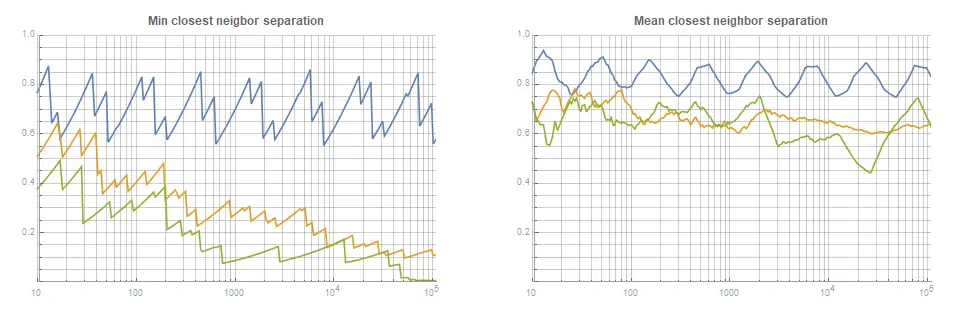
Рисунки 6а, 6б.
Метрика ближайшего соседа для ряда
(синий); Холтон (оранжевый); и Соболь (зеленый).
Все показанные расстояния представляют собой абсолютные расстояния между ближайшими соседями, умноженные на
.
Обратите внимание, что строка
является единственным, чье минимальное расстояние падает со скоростью всего
, в остальном оно падает со скоростью примерно
.
Он также имеет самое большое среднее расстояние для всех значений.
.
Используя этот подход, критический радиус колебаний для
, Холтон и Соболь, показаны в таблице ниже.
Соответствующие им распределения точек показаны на рис.
5. Заметим, что для ряда Соболя флуктуация должна уменьшаться гораздо медленнее, чем
, чтобы замаскировать весьма отчетливые артефакты, поэтому я не рекомендую его для какого-либо применения, но я все равно представил его для полноты картины.

На рисунке 7 показано, что флуктуация R2, флуктуация Холтона и даже флуктуация Соболя создают распределения изотропных точек синего шума.
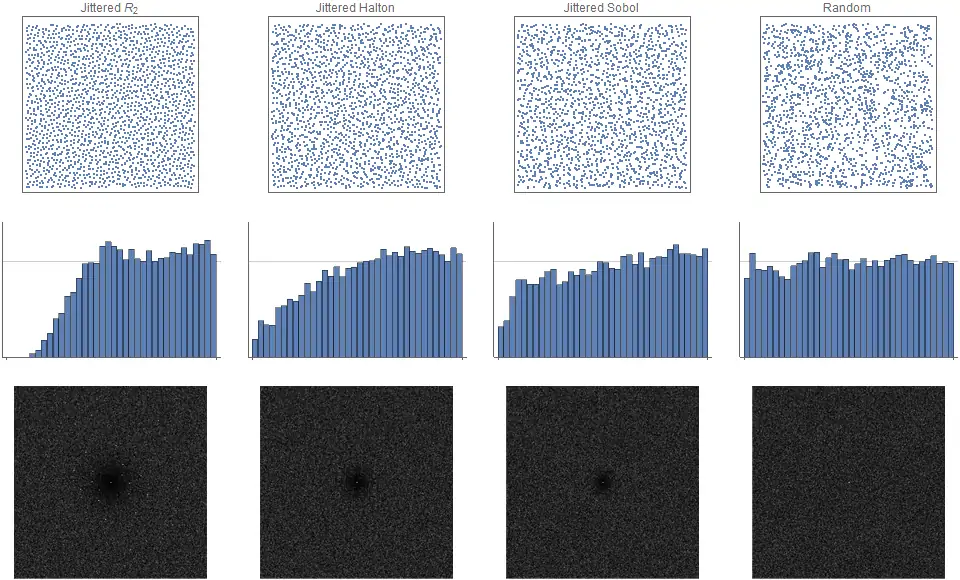
Рисунок 7. Наборы флуктуаций точек (n=2000) на основе различных псевдослучайных рядов: (i)
, (ii) Холтон; и (iii) Соболь, с (iv) случайным образом для сравнения.
Обратите внимание, что преобразование Фурье для всех псевдослучайных версий теперь изотропно с небольшими, но заметными признаками синего шума.
Также обратите внимание, что колебания серии Соболь должны быть намного больше, чтобы замаскировать очень большие артефакты.
Стоит отметить, что радиальные спектральные функции флуктуации R2 и флуктуации Холтона кажутся похожими на рандомизированные и флуктуационные сетки Оуэна (не показаны), но их спектры Фурье сильно различаются.
Стоит отметить, что для
критический уровень колебания мы можем определить и другим способом - как максимально возможный уровень колебаний, обеспечивающий нулевое значение радиальной спектральной функции для самых низких частот .
Эмпирически это определение дает нам
схожее значение
, но соответствующие уровни для Холтона и Соболя будут гораздо ниже указанных в таблице, и должны падать со скоростью
, но нет
, как и в случае
.
Из-за желаемых спектров Фурье часто необходимо построить наборы точек с хорошим разделением между соседними точками.
Ниже приведены минимальные и средние расстояния для n=500 точек с использованием различных методов.
Данные, отмеченные звездочкой, взяты из статьи «Progressive Multi-jittered Sample Sequences» [ Кристенсен, 2018 г.
], а новые результаты выделены жирным шрифтом.
(Стандартные данные для Холтона и Соболя, а также общие данные для случайного ряда).
Данные представлены в порядке убывания среднего расстояния.

Также стоит помнить, что расхождение формально является показателем, зависящим от площади.
Он измеряет разницу между плотностью числа точек в произвольной (прямоугольной) области распределения точек и плотностью точек, распределенных в однородной решетке.
В общем, строки с низкой дивергенцией обычно связаны с хорошими показателями сходимости.
В отличие от дивергенции, метрики разделения точек основаны на длине.
Интуитивно понятно, что распределения с хорошим разделением точек имеют тенденцию иметь низкую дивергенцию, и наоборот. Поэтому на практике эти понятия очень близки и часто (произвольно и неправильно) используются как синонимы.
Однако иногда между этими разными понятиями могут возникать тонкие различия.
Оптимальная серия точек с низким расхождением может иметь хорошо, но не оптимально разделение точек.
И наоборот, ряды с идеальным разделением точек могут иметь хорошо, но несовершенно расхождение.
Другими словами, «лучшие образцы дисков-кандидатов имеют хорошее распределение пространства между точками, но неравномерное распределение в целом» [ Кристенсен, 2018 г.
].
Это может помочь нам получить более глубокое интуитивное понимание того, почему ряд Соболя имеет отличные показатели сходимости, но только хорошее разделение точек; и почему аппроксимированная дисковая выборка может иметь почти оптимальные характеристики синего шума, но лишь приличные показатели сходимости.
Также стоит отметить, что, судя только по метрике разделения минимальной и средней точки, может показаться, что флуктуационные ряды Холтона на практике бесполезны и неотличимы от случайного шума.
Однако из рисунка 4 хорошо видно, что ряд флуктуаций Холтона показывает меньшую
Теги: #математика #Алгоритмы #Метод Монте-Карло #рендеринг графики #артефакты #псевдослучайность #синий шум #бесконечный ряд #конвергенция
-
Почему Моя Тема Видна Только Мне?
19 Oct, 24


