В предыдущем ряд Мы рассмотрели дробные числа, в состав которых не входят рациональные числа.
Сегодня нас ждет именно эта часть, которая не рассматривалась, а также будем готовиться к чуть более сложной заключительной части без привлечения таких терминов, как кольца классов вычетов или сравнения по модулю с дискретными логарифмами.
Также в третьей части желающих ждут призы в размере $400K. Почему в третьем? Потому что без введения в тему не всегда легко понять причины, по которым призы не так просто получить.
А после прочтения - просто удача и целеустремленная, терпеливая, но не очень трудная деятельность, вот и все, что вам нужно.

Рациональные звезды
Чтобы ответить на ранее заданные вопросы о рациональных числах, нам снова понадобится небольшое отступление.Во-первых, помните, что в процессе деления на «угол» мы постоянно получаем остаток от деления какой-то части числа, делимого на делитель.
В этом случае в результат записывается вся часть деления, а остаток деления умножается на основание системы счисления, после чего процедура деления с остатком повторяется до тех пор, пока не будет обнаружен период или все делители уменьшаются и мы получаем конечную дробь.
Это выглядит так:
Здесь остаток от вычитания 18 из 20 всегда равен двум, которые мы затем умножаем на основание десятичной системы счисления.5 | 3 ------ 1.66(6) 3 20 18 20 18 2 .
Теперь давайте подумаем, чем деление 5 на 3 отличается, например, от деления 1 на 3? Ответ прост – наличие в результате целой части.
Но нас интересует период и та часть, которая предшествует периоду (называемая предпериодом), но не входит в целую часть результата.
Поэтому нам нет необходимости рассматривать всю часть.
Это означает, что в данном примере мы можем исключить из рассмотрения все числа, большие 3 или равные ему.
И что еще более интересно, законы деления в большинстве случаев фигурируют без какого-либо другого числа, кроме единицы.
То есть достаточно изучить деление единицы на ряд целых чисел, больших единицы, и мы с вами поймем, как ответить на все заданные вопросы, а заодно познакомимся с очень приличным количеством новых звезд. .
Пока мы не приступили к серьезному изучению предмета, вот несколько хитростей.
Знаете ли вы, что можно делить «наоборот»? Не так, как мы привыкли со школы, а начиная с конца.
Покажем это на другом примере, в котором мы берем последний остаток и, исходя из него, вычисляем период дроби.
Вспомним, что остаток при делении 5 на 3 был равен 2. Какое число мы вычитали последним, чтобы получить два? Нам не нужно запоминать, потому что мы знаем, что всегда вычитаем числа из предыдущего остатка, умноженного на 10, то есть последняя цифра уменьшаемого всегда равна 0. Это значит, что достаточно перебрать произведения тройки чисел от 1 до 9, =(3,6 ,9,12,15,18,21,24,27), увидеть - среди них только одна оканчивается на 8 и при добавлении к остатку 2 дает ноль в последней цифре уменьшаемого.
Это значит, что прежде чем получить остаток 2, мы из 20 вычли 18. Почему из 20? Потому что любое другое число с нулем в последней цифре даст разницу Х0-18 больше трёх или меньше нуля.
Аналогично вычисляем все остальные числа: 2 - известный остаток 18 - добавление к числу с нулём, одновременно показывающее значение следующей цифры результата - 6 (6*3=18) 20 — подходящее число с нулем 2 - число с нулём перед умножением на 10 (=20/10) 18 – это дополнение числа с нулём.
20 — подходящее число с нулем … В результате мы получим точно такую же последовательность, как и при делении углом, но «на другой стороне».
Таким образом можно вычислить «с конца» период любой периодической дроби.
А что такое предпериод (и нецелесообразность его расчета для данного случая показанным методом) мы увидим далее.
Целая часть результата всегда равна нулю при использовании единицы в качестве делимого, поэтому нам снова не нужно вычислять что-либо еще, кроме периода.
Теперь вспомните, как мы делим одно на три:
.
Здесь все просто, период короткий, предменструального периода нет, вроде бы ничего примечательного.
Но давайте попробуем еще раз умножить результат деления на три:
, то есть
.
А вначале было так:
.
Не замечаете разницы? На входе стояла единица, и после прямых и обратных действий получаем.
Как это проще назвать? То есть, если проследить всю цепочку девяток до бесконечности, то мы поймем, что перед нами одна, но все равно она как-то не та, вам не кажется? Ну не похоже на оригинал, вот и всё.
Математики скажут, что это всего лишь две формы записи одного и того же числа, но повседневное понимание «одного и того же» несколько восстает против таких определений.
В принципе, с математиками трудно не согласиться, ведь многие девятки после запятой отличаются от единицы чем-то совершенно эфемерным, бесконечно малым и стремящимся в пределе к нулю.
А конкретно, можете ли вы постичь в своих мыслях весь этот набор бесконечностей? Бесконечное количество девяток, бесконечно малая разница, стремящаяся к нулю при движении по ряду девяток к бесконечности.
А теперь сравним это с этой записью - 1. Один знак - и нам все ясно.
Сколько знаков было в рассуждении о равенстве бесконечного числа девяток одной? Значит, разница все-таки есть? Или ваш мозг легко игнорирует такие мелочи в наборе различий? Но если мы не дойдем мысленным взором до бесконечности в списке девяток, то в том месте, где мы остановимся, сразу возникнет разница, которую даже математики признают существенной – если мы не увидим все остальные девятки, то мы вообще ни на что не смотрим.
Поэтому возникает вопрос – можете ли вы видеть на глубину всю бесконечность? В общем, как хотите, математики распорядились считать это явление одним и тем же числом.
Поэтому, рассмотрев эту звезду (с, прямо скажем, странным свечением), перейдем к следующей.
Из открытия бесконечного числа девяток следует интересный вывод – если делителем единицы является простое число, большее 3, то полученный период всегда делится на 9, и конечно на 3, а также, если его длина больше чем один знак - по 11, а когда и больше символов - 13, 37, 101 и так далее.
И это все независимо от делителя единицы, лишь бы он был простым и больше трех.
Вы можете проверить это самостоятельно, например, разделив период 1/7, равный 142857, на 3, 9, 11, 13, 37. Ну и перед Кучмой зададим себе простой вопрос - можно ли построить период самостоятельно? Да, ты можешь.
Например, мы хотим получить период 0123456789, можем ли мы найти делимое и делитель, которые дают нечто подобное? Может! Но без цифры 8. Тогда будет 1/81. А чтобы число 8 появилось на своем законном месте, нам нужно будет к числу 81 добавить довольно много цифр после запятой или без запятой, но тогда в точке будет много нулей.
Другая закономерность заключается в том, что для некоторых делителей единицы мы можем вообще не вычислять период, а просто циклически сдвигать его при умножении делимого (единицы) на какое-либо число.
Например - 1/7=0.(142857), а 2/7=0.(285714), 5/7=0.(714285), 3/7=0.(428571) и так далее.
Если делимое больше 7, то вся часть результата деления уйдет в часть до запятой, а период все равно будет состоять из тех же шести цифр, но опять же циклически сдвинутых - 25/7=3.( 571428), 86/7=12. (285714) и т. д. Как вам это? Любое число при делении на 7 дает набор одинаковых цифр! Что-либо! Абсолютно что угодно.
И да, этих «любых чисел» — бесконечное число.
И результат всегда включает одни и те же 6 цифр.
Дальше вы поймете, почему мир чисел устроен именно так, а пока отметим, что при делении единицы на 7 мы неявно получали абсолютно всю необходимую информацию для расчета периода из результата деления любых других чисел на семь, поскольку мы теперь знаем, что достаточно просто циклически сдвинуть один единственный результат деления.
То есть еще раз подтверждается, что на выбранное для исследования число делить никакие числа, кроме единицы, не нужно.
Правда, возможно, придется умножить на какие-то числа и запомнить промежуточные результаты, но об этом позже.
Теперь, чтобы получить более общее представление, покажем «карту боя».
Составляется карта деления единицы на изучаемое число, причем деление производится во всех системах счисления с основанием меньшим, чем изучаемое число.
На карте не указан результат деления, то есть период рассматриваемой дроби, а вместо этого на карте показаны остатки, полученные на каждом этапе деления на «уголок».
Вот как это выглядит: 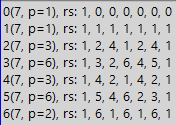
В таблице ниже вы видите строки от 0 до 6. 0 также является основой системы счисления.
Вы не согласны? Давайте попробуем вас убедить.
Что такое система счисления? Это база, умноженная на определенное значение, а затем прибавленная к результату, который в самом начале равен нулю.
Именно так получаются все числа, например, в десятичной системе счисления.
Что, если база равна нулю? Тогда все члены, умноженные на ноль, также будут равны нулю.
Но какая разница? Нарушили ли мы правило построения чисел в выбранной системе счисления? Поэтому для общности картинки на карте сражения мы используем все системы счисления, от 0 до 6 в случае изучения числа 7. Но помимо общности линия с нулями будет иметь и дополнительное назначение.
Но что означают все эти строки? Каждая строка показывает нам последовательность остатков при делении единицы на число семь в системе счисления, подписанное в крайнем левом столбце.
То есть при делении 1/7 в системе с основанием 0 мы имеем начальный остаток 1 (единицу, которую мы делим).
Далее, как мы всегда делали при делении на угол, умножаем первый остаток на основание системы счисления.
Мы получаем ноль.
Теперь ноль — это текущий баланс.
Обычно при вычислении частного после получения остатка, равного нулю, и если в делимом числе нет дополнительных цифр, деление прекращают (так как получен результат).
Но в нашем случае мы заполняем таблицу, которая не терпит пустоты и помимо нетерпеливости обладает дополнительными свойствами, которые также требуют наличия каких-то чисел во всех ячейках.
Поэтому продолжаем деление и делим остаток 0 на 7. Обычно, пока остаток меньше делителя, его умножают на основание системы счисления, но много раз умножать на ноль бесполезно, поэтому просто пишем что после умножения на ноль остаток снова станет нулевым, и теперь поместим его в таблицу в соседнюю ячейку.
Затем повторим процедуру.
И так заполняем нулями все ячейки первой строки.
А затем заполним вторую строку.
Но у него уже другое основание системы счисления – одно.
После деления 1 на 7 имеем первый остаток – единицу.
Затем умножаем на основание системы счисления, то есть на единицу.
Мы снова получаем 1. Напишите в соответствующую ячейку.
Снова умножаем на 1, снова получаем 1, снова пишем.
И так до тех пор, пока не заполнится вторая строка.
Но после этих двух замечательных во всех отношениях строк мы наконец доходим до более осмысленного деления – по двоичной системе (и смысл первых двух систем станет ясен позже).
Во-первых, у нас все еще есть тот же блок.
Давайте напишем его в третьей строке.
Затем умножаем на основание системы счисления (на 2).
Получаем 2. 2 меньше семи, вычесть его пока нельзя, поэтому запишем остаток 2 в таблицу.
Умножаем еще раз на 2, получаем 4, что опять меньше 7, а значит снова попадает в таблицу без изменений.
Но на следующем шаге мы получаем 8, что больше 7, а значит, нужно вычитать.
Результат – 1. Запишите в таблицу.
Но раньше у нас уже была такая, поэтому все остальные шаги будут такими же — поэтому добавим в конец третью строку.
И точно так же сложим остальные строки, но не забывая, что умножать нам нужно на другое основание системы счисления.
Итак, когда у нас наконец-то будет заполненная таблица, мы сможем сделать некоторые выводы.
Давайте сначала посмотрим на повторы.
Для двоичной системы имеем 1,2,4,1,2,4,1, то есть два раза 1,2,4 и потом еще один раз 1. Здесь список 1,2,4 соответствует периоду полученная двоичная дробь.
То есть период будет иметь длину 3. И хотя вместо чисел от периода мы использовали остатки, длина от этого никак не пострадала, а потому вся информация сохранилась.
И даже больше – в таблице на самом деле осталось больше информации.
Но об этом чуть позже, а пока отметим, что все линии сделаны одинаковой длины для удобства изучения и потому, что такое представление имеет ряд полезных свойств.
Итак, линии начинаются и заканчиваются единицами, что ярко подчеркивает свойства числа 7. И если бы мы сократили линии до длины точки, мы бы не смогли насладиться такой красотой симметричного отображения сути числа.
номер 7. Теперь об информации.
Остатки однозначно определяют цифру в соответствующей позиции периода, поэтому информация в этом представлении не теряется, но поскольку остатки могут быть больше, например, максимум одной десятичной позиции (т.е.
9), то информация с их участием становится наиболее полная, потому что одна позиция в системе исчисления не может сказать нам, что остаток составил, например, 19, но остаток 19 ясно скажет, какая цифра находится в периоде и из какого предыдущего остатка мы вычли произведение делимого ( вспомните фокус с делением «с конца»).
И кроме того, мы сразу замечаем одну простую вещь – остатков не может быть больше, чем
, Где
– изучаемое число, на которое делим единицу.
Это очень важный момент. Кроме того, легко доказать, что если при делении на угол повторить встретившийся ранее остаток, то произойдет повторение всей последовательности остатков, которые ранее следовали за повторяющимся значением.
Это значит, что нам больше не нужно считать, так как период найден.
Если мы записываем только числа из точки, то повторение числа в точке не означает завершения расчета.
Поэтому балансы важнее цифр за период. Но самое интересное - это остатки всего
, и, следовательно, периоды длиннее
Не может быть.
Вот так мы просто нашли верхнюю границу количества цифр в периоде, двигаясь от собственно цифр периода к остаткам.
Как говорится, легкое движение руки и никакого мошенничества.
Так демонстрируется преимущество более полной информации.
Ну, вот почему ширина нашей «карты боя» для 7 равна 6+1 столбца, то есть 6 столбцов для всех возможных остатков и 1 столбец для обнаружения симметричности единиц, что отнюдь не обязательно для всех чисел, и, следовательно, его не следует скрывать, чтобы сэкономить место для одного столбца.
Что ж, теперь давайте посмотрим на приведенную выше «карту» с точки зрения ее полезности.
Сразу можно заметить набор простых закономерностей.
Каждая строка начинается с единицы и заканчивается ею.
Вторая позиция каждой строки указывает основание системы счисления, а середина каждой строки содержит либо N-1, либо 1. Обратите внимание, что мы не пытались расположить числа в таблице в указанном порядке, кроме простой записи Результаты деления представлены в таблице.
Но несмотря на наше игнорирование любого приказа (кроме последовательности шагов деления), сам приказ возник из ниоткуда и нарисовал нам букву П из единиц, поставил на нее колпачок из нулей (с козырьком из единиц), разделил таблицу со средним столбиком единиц и его дополнением к числу 7 (по формуле 7-1=6).
Кроме того, сам приказ поместил во второй столбец номера систем счисления.
Сравните его с цифрами в самом первом столбце слева, они добавлены намеренно, чтобы мы точно знали, какая система счисления какая.
Ну а период получившихся дробей мы легко можем вычислить сами, хотя для удобства он указан в столбце со значениями вида p = X. По сути, это что-то вроде таблицы Менделеева, только не для химии, а для теории чисел.
Так же, как и Менделеев, можно просто посмотреть на таблицу, чтобы обнаружить определенную закономерность, а затем, как и после Менделеева, наличие этой закономерности можно обосновать и доказать, что она повторяется для всех чисел, удовлетворяющих определенному набору уравнений.
условия.
И это самое главное в таких таблицах.
Просто рассматривая и наблюдая закономерности, вы можете открыть законы, например, теории чисел.
Ну а для более вдумчивых читателей здесь открывается дорога к полному циклу – найдя закономерность, нужно потом доказать (или опровергнуть) ее актуальность для всех чисел, либо для чисел определенного класса.
Как уже отмечалось, эта таблица содержит полную информацию о простом числе 7. Но на основе этой информации можно вывести гипотезы обо всех простых числах.
И даже некоторые из этих гипотез до нас уже доказаны, так что нам остаётся только проверить выводы других людей.
Доказательства давали такие известные люди, как, например, Ферма и Эйлер.
Ферма дал нам эту формулу
(здесь операция мод берет остаток от деления значения слева на значение справа, в программировании это обычно обозначается знаком %), то есть остаток от деления
на p всегда равен единице для всех простых чисел (именно простых чисел, это важно).
Но число 7 тоже простое.
А каждый остаток в каждой строке можно рассчитать по следующей формуле:
.
Здесь b – основание системы счисления (от английской основы), i – номер позиции в строке (от английского индекса), начиная с нуля для первой позиции, N – изучаемое число (в данном случае 7), r — остаток (от англ.
напоминания), образующийся на i-м шаге деления на угол и содержащийся в i-м столбце таблицы.
Сравним формулу Ферма и формулу вычисления остатка, заданного индексом i. Они идентичны для последнего члена всех последовательностей остатков.
И в полном соответствии с формулой Ферма для каждого остатка в позиции
у нас есть равенство единице.
То есть закономерность, наблюдаемая невооруженным глазом в виде столбика единиц, была подтверждена и доказана еще во времена Ферма (хотя Ферма не баловал нас доказательствами, но обычно все его утверждения были правдой).
«Илер добавил к формуле Ферма возможность использовать ее не только для простых чисел, но и для составных чисел.
Правда, нужно знать все делители числа, но для небольших чисел это не проблема.
Итак, во второй таблице (ниже) мы видим последовательности остатков числа 21, которое является составным числом.
Айлер доказал, что остаток от деления произвольного числа в степень, равную количеству чисел, меньших и не имеющих общих делителей с N, также равен единице.
И именно этот факт мы наблюдаем в таблице для числа 21, у которого из 20 меньших чисел 8 имеют общий делитель с 21, а 12 — нет. Поэтому мы видим много единиц в 12-м столбце (при индексации с нуля).
И эти единицы не находятся в конце строк, потому что некоторые числа, меньшие 21, имеют с 21 общие делители.
Но для простых чисел ни одно меньшее число не имеет с ними общих делителей, поэтому число чисел без общих делителей для простых чисел всегда больше, чем для составных чисел.
И поэтому одиночные остатки в таблице у простых находятся дальше, чем у сложных.
Но учтите, что не все значения в 12 столбце таблицы для 21 равны единице.
Ошибся ли Эйлер? Нет, он просто не собирался использовать свою формулу для работы с числами, которые можно сокращать, и именно в строках, кратных 3 и 7 (делителям числа 21), мы имеем расхождение с формулой Эйлера.
В общем, оказывается, что Ферма и Эйлер дали нам подходящие формулы, полезные для понимания задач делимости чисел, а приведенные таблицы во всей красе подтверждают результаты Эйлера и Ферма.

Хотя стоит отметить, что ни Ферма, ни Файлер не знали о приведенной выше таблице.
А если и знали, то никому об этом не говорили.
Хотя, с другой стороны, в их времена альтернативные десятичные системы счисления были несколько менее популярны, чем в наше время.
В то время еще не все знали о десятичной системе; они могли только пересчитать по пальцам.
И поэтому формула, выведенная Ферма, а затем расширенная Эйлером для связи основания и степени, не дает нам объяснения остальных закономерностей этой таблицы.
Поэтому нас ждут новые звезды, а затем период условного открытия электронных оболочек атомов, с помощью которых химики наконец объяснили магические предсказательные свойства таблицы Менделеева.
Но начнем с магии.
От звезд к волшебству
Любителям головоломок знакомы так называемые «магические квадраты».Это таблицы, в которых нужно расположить числа таким образом, чтобы суммы по вертикалям, горизонталям и двум диагоналям были одинаковыми.
Многие люди долго и упорно ломали голову над тем, чтобы уместить цифры в прокрустово ложе пределов сумм, и даже сумели заполнить довольно большие квадраты.
Но сегодня мы знакомимся с гораздо более могущественной магией.
Да, таблица Менделеева по теории чисел содержит гораздо больше ограничений, и заполнить ее сможет даже первоклассник, который научится делить «уголком».
Вдумайтесь — умнейшие люди заполняли магические квадраты, но так и не нашли общего метода их заполнения и не продвинулись в размерах даже до жалкой сотни столбцов.
Первоклассник легко справится даже с миллиардом, если у него будет достаточно времени.
Это такая галактика, доверху набитая звездами, ожидающими нас в числовых квадратах.
Начнем перечислять очевидные закономерности.
Умножение.
Любую строку таблицы можно умножить на любую другую.
Результатом будет ряд, количество которого рассчитывается как произведение чисел умноженного ряда, разделенное с остатком на изучаемое число.
То есть, если умножить 2 строку таблицы для 7 на 3 строку, то получим 6 строку.
А если 4 строку умножить на 6 строку, то получим 24 по модулю 7 = 3, то есть третью строку.
А само свойство деления по модулю (то есть с остатком) делает ненужными все системы счисления, большие, чем изучаемое число.
Так что система счисления по основанию 24 нам не нужна, так как значения остатков в ней будут точно такими же, как и в системе счисления по основанию 3. В какой бы системе счисления мы ни вычисляли остатки от деления 1/7, мы всегда получим результат, который уже есть в таблице.
Интересный? И это только начало.
Симметрия.
Каждый второй столбец содержит верхнюю и нижнюю части, которые являются отражением друг друга.
А остальные столбцы содержат значения, равные дополнению N отраженного остатка.
То есть во втором столбце таблицы для числа 7 цифра 1 дополняет 6 до 7, 2 дополняет 5 и 3 дополняет 4. В результате формула, рассмотренная выше
дополнена следующей системой:
, для нечетных столбцов
, для четных столбцов
Здесь N — изучаемое число (например, 7), b — основание системы счисления, i — индекс столбца, начиная с нуля, r — значение остатка в заданных b и i ячейке.
По горизонтали симметрия выражается ранее упомянутыми внешними столбцами единиц и средним столбцом единицы и ее дополнениями к N. Это работает точно только для простых чисел, но для составных чисел есть отклонения.
При этом (опять же только для простых чисел, но иногда и для составных чисел) разделяющий средний столбик всегда либо начинается с единицы для повторения имевшего место остаточного периода, либо дает ряд прибавок справа к N для левой половины из серии.
То есть если в среднем столбце стоит единица, то повторяется левая часть.
Если есть прибавление к N, то следующей идет та же левая часть, но после вычитания из N. Таким образом, из всей таблицы (для простых чисел) можно оставить только левый верхний квадрат со стороной
(без нулевой строки), а все остальные остаточные значения однозначно выводятся на основе информации из такого квадрата.
Хотя не следует забывать, что в целом вся таблица выводится на основе знания одного-единственного числа – делителя, при этом делимое – это константа, равная 1. Теперь суммы.
В основном для простых, но иногда и для сложных соблюдают следующие правила.
Горизонтальная сумма (без добавления последнего столбца для ясности) всегда кратна изучаемому числу.
Вертикальная сумма также всегда кратна изучаемому числу.
Суммы остатков внутри периода от одного до одного (период может быть меньше ширины таблицы) также кратны или равны изучаемому числу.
Далее идет делимость.
Ряды остатков между единицами (периоды остатка) могут иметь разную длину, но все длины рядов для простых чисел всегда делят общую длину таблицы на целое число.
То есть, если хотя бы одна строка между единицами не делит общую длину таблицы целиком, то перед вами составное число (сравните таблицы для 21 и 7).
Длина и уникальность.
Каждая строка четной длины и короче ширины таблицы состоит из двух частей — ряда остатков до середины, за которым следует ряд прибавлений к N для исходного ряда остатков.
При этом все значения внутри периода уникальны, то есть повторяются только при повторении периода, но внутри периода они никогда не повторяются.
Умножение.
Если каждую ячейку таблицы умножить на целое число, то получим либо циклический сдвиг остатков в случае длины периода, равного ширине таблицы, либо новую строку в случаях, когда период короче ширины таблицы.
стола.
При этом в случае коротких периодов все значения в новом ряду будут уникальными, то есть ни одно из них не находится в ряду, полученном делением единицы на изучаемое число, а также в ряду получается умножением на другие числа и в исходном ряду, который мы умножили на константу.
Общее количество уникальных периодов равно ширине таблицы, деленной на длину периода (для простых чисел).
А для составных чисел во всех возможных периодах нет «запрещенных» остатков, которые при умножении на ряды, кратные делителям изучаемого числа, дают нулевой остаток, но об этом чуть позже.
В результате перемножения ряда можно получить либо циклический сдвиг периода, либо новый период. Новый период также можно циклически сдвигать, умножая его на другие значения.
Общее правило выбора смены или нового периода простое – если в остаточном периоде есть число, на которое мы умножаем, то мы получим циклический сдвиг, а если такого числа нет – получим новую серию.
.
И конечно, это напрямую относится к периодическим дробям, точнее к их периодам (периоды из остатков следует отличать от периодов из цифр в обозначении дроби, хотя обычно разница понятна из контекста).
Итак, на показанном ранее примере числа 7 мы увидели, что как бы мы не умножали результат деления на 7, мы всегда получим один и тот же набор чисел в периоде, но циклически сдвинутый относительно исходного деления 1/ 7. В случае числа 7 мы имеем период (в десятичной системе счисления) с длиной, соответствующей ширине таблицы, поэтому никаких других цифр в нем получить нельзя (остатков больше нет), а только возможны циклические сдвиги.
Но есть еще один момент – мы делили в десятичной системе, а в таблице такой строки нет. Это значит, что для его нахождения нам нужно разделить 10 на 7 и получить остаток — 3. Именно система счисления с основанием 3 полностью повторяет поведение десятичной системы по отношению к остаткам, поэтому именно в третьем ряду находится мы видим полный период, то есть длину, равную ширине стола.
А чтобы из остатков получить период в десятичном выражении, можно взять любой остаток и начать делить его с углом, тогда результатом будут все цифры периода дроби.
Сдвиг периода при умножении определяется путем нахождения остатка при делении множителя на N в ряду остатков.
Сдвиг будет равен индексу найденного остатка, то есть нам всегда нужно циклически сдвигать период справа налево на количество цифр, равное индексу найденного остатка.
И несколько зависимостей между различными изучаемыми числами: 
Здесь мы видим ряды для чисел от 2 до 39 в двоичной системе.
Обратите внимание на нижний ряд. От него вверх поднимаются столбцы цифр 1,2,4,8,16,32. После числа 32 мы видим столбец значений, увеличивающихся на единицу (25,26,27,.
).
В следующем столбце значения увеличиваются на три.
Затем на 6, 13, 26 и т. д. Прибавка «переключается» после достижения значения, большего изучаемого числа (столбец слева в скобках, перед длиной периода).
Так рост на единицу переключается на рост на два, затем на три и т. д. Вообще все такие столбцы начинаются с
, где i — индекс столбца.
Ниже
значение не меняется, а выше изменяется в соответствии с формулой
, где j — приращение при сдвиге вверх по строке (больше нуля).
То есть, пока номер строки находится между
И
, приращение равно j. После пересечения границы
, приращение будет равно
, то граница будет
Теги: #Научно-популярные #математика #число #делимость #дроби #остатки

-
Роуленд, Шервуд
19 Oct, 24 -
Легче, Чем Кажется. 20
19 Oct, 24 -
Iriver E50 «В Металле»
19 Oct, 24


