Привет Хабр! По основной профессии я инженер по разработке месторождений нефти и газа.
Я только погружаюсь в науку о данных, и это мой первый пост, в котором я хотел бы поделиться своим опытом использования машинного обучения в нефтяном секторе.
Прогнозирование добычи нефти и газа является одной из важнейших задач нефтегазовой отрасли.
Без обоснованного прогноза добычи невозможно принимать решения о рентабельности проектов, капитальных вложениях, бурении новых скважин и оперативном планировании эксплуатации существующих скважин.
В этой статье я хочу поделиться своим опытом создания модели машинного обучения применительно к нефтегазовому сектору.
Целью построения модели было прогнозирование одного из параметров работы скважин и проверка способности модели прогнозировать обводненность существующих скважин и скважин, которые планируется к бурению (кандидатов на бурение).
Данные о добыче фактически представляют собой временной ряд, который требует построения более сложной модели.
В целях упрощения и ускорения было решено построить модель под конкретно выбранную дату.
Обзор: как прогнозируется добыча нефти и газа
На данный момент, помимо классического аналитического метода оценки (Excel + метод математического баланса), общепринято строить геологические (статические) и гидродинамические (динамические) модели, на основе которых принимаются решения.Геологическая модель строится на основе скважинных данных (обычно с использованием сейсмических данных).
Сначала строится трехмерная сетка (каркас) продуктивных пластов.
Далее каждой ячейке сетки присваиваются такие свойства породы, как пористость, проницаемость, водонефтегазонасыщенность, давление и другие.
После этого на основе статической модели рассчитывается динамическая модель, которая отличается от геологической тем, что рассчитывает, как изменяются указанные выше параметры ячейки во времени в зависимости от объема добычи скважин и наоборот. Динамическая модель помогает ответить на вопрос, где бурить новые скважины и сколько нефти можно добыть.
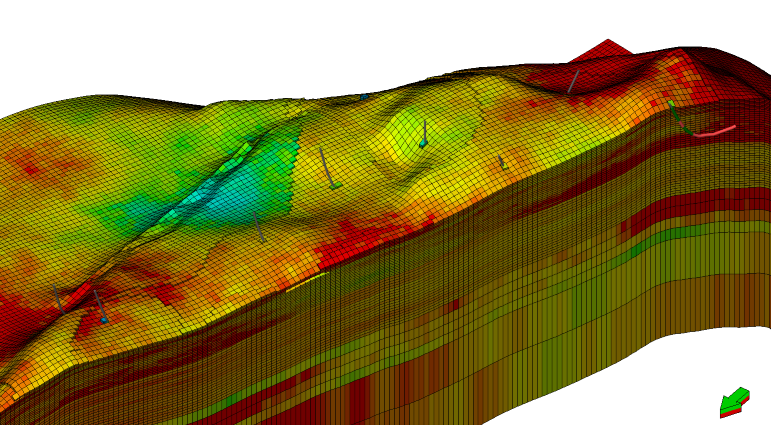
Гидродинамическая модель в 3D представлена на самой первой картинке (вверху).
Недостатком подхода к построению полноценной гидродинамической модели является то, что построение модели занимает много времени (от нескольких месяцев до года и даже больше).
Это зависит от количества скважин и имеющихся полевых данных.
При этом построенная гидродинамическая модель представляет собой сложную систему с высокой чувствительностью к входным данным.
Поэтому любая неточность в данных может привести к неверным результатам.
Неудивительно.
Протяженность залежей достигает десятков километров.
А типичный диаметр колодцев находится в пределах 10 – 15 см.
Скважины, в свою очередь, бурятся на глубину около 3 километров и на расстоянии 250 – 1000 метров друг от друга.
Таким образом, модель построена на крайне ограниченных данных, которые можно охарактеризовать как «точечные инъекции».
Колодец обычно представляют собой яму в земле.
Это не совсем правда.
Классическое определение колодца звучит так.
Колодец представляет собой цилиндрическое шахтное отверстие, во много раз длиннее его диаметра.
.
Обычно это 3-километровая скважина (иногда, конечно, больше, иногда меньше) скважина, в которую опускаются несколько колонн обсадных труб, вложенных друг в друга (для предотвращения обрушений).
Пространство между обсадными колоннами и породой цементируется для герметичности.
На поверхности устанавливается елочная сборка, которая изолирует колодец от окружающей среды.
Скважины бурят не только для добычи нефти и газа.
Подавляющее большинство данных о недрах добывается из скважин.
Данные скважины включать:
- данные, полученные при спуске приборов в скважину (например, давление, температура, глубина залегания нефте/газонасыщенного пласта, кажущееся сопротивление горных пород, радиоактивность и т.д.),
- измеренные на поверхности - количество добытой нефти, газа и попутной воды, их состав.
В этой статье речь пойдет о нефтяных скважинах.
Это означает, что на поверхность мы получаем нефть с растворенным в ней газом и попутной водой.
Как правило, в начале эксплуатации скважины добывается чистая нефть, но в дальнейшем скважина обводняется и доля воды увеличивается.
Когда доля воды увеличивается, а доля нефти снижается до определенного предела, скважина перестает быть рентабельной и закрывается.
Обводненность выражается в процентах и рассчитывается как отношение количества попутной воды к добытой жидкости, т.е.
Qoil/(Qoil + Qwater)*100% Типичный профиль добычи нефти с течением времени (в данном случае по годам) выглядит следующим образом: 
Построение модели
В качестве входных данных для обучения модели были выбраны следующие параметры скважины:- Кумовая нефть: совокупная добыча нефти
- Дни: количество дней работы скважины (до момента полива (и ее остановки по причине нерентабельности) или до текущего момента, если скважина находится в эксплуатации).
- В проде: скважина в работе/остановлена из-за полива
- Q Oil: текущий расход масла.
- wct: текущая обводненность
- Top perf: глубина верха интервала перфорации - глубина верха и низа
- Bottom perf: глубина дна интервала перфорации.
- СТ: 0 - основной ствол скважины, 1 - боковой ствол скважины
- x, y: координаты скважины
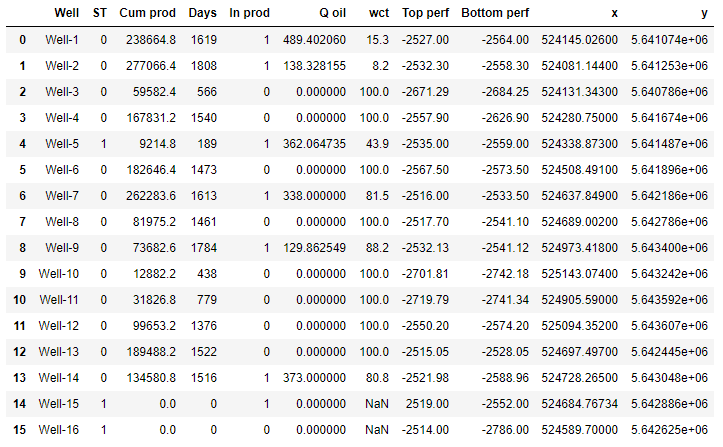
Мы загружаем исходные данные на определенную дату из Excel и визуализируем фрейм данных.import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline %config InlineBackend.figure_format = 'svg' import pylab from pylab import rcParams import plotly.express as px import plotly.graph_objects as go from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import r2_score as r2, mean_absolute_error as mae, mean_squared_error as mse, accuracy_score from sklearn.metrics.pairwise import euclidean_distances
data_path = 'art_df.xlsx'
df = pd.read_excel(data_path, sheet_name='artificial')
df
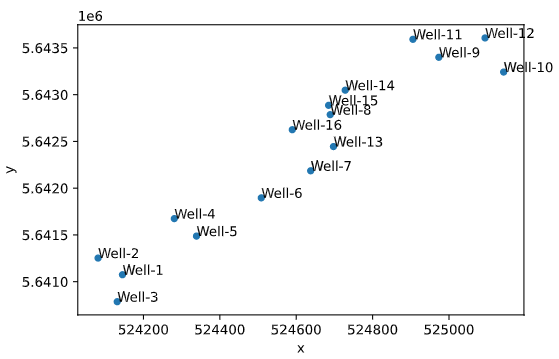
Проверяем расположение скважин - строим карту расположения скважин.
В данном случае это карта забоев (нижних точек заканчивания скважин).
ax = df.plot(kind='scatter', x='x', y='y')
df[['x','y','Well']].
apply(lambda row: ax.text(*row),axis=1);
rcParams['figure.figsize'] = [11, 8]
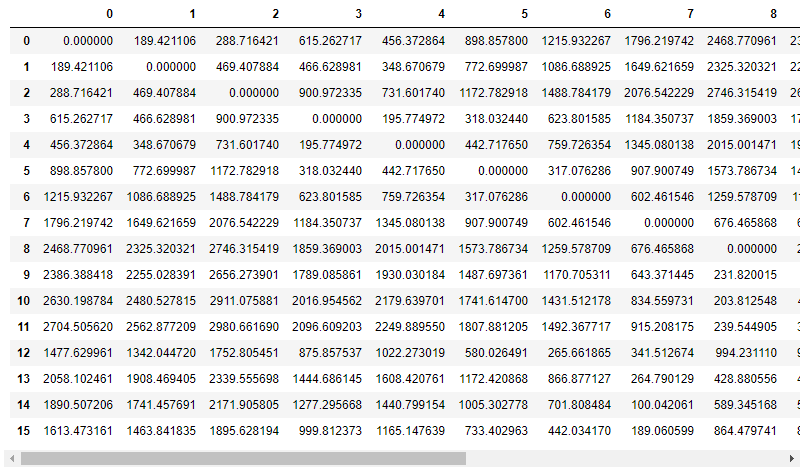
В процессе построения модели было обнаружено, что загрузка координат скважины в модель «как есть» работает хорошо.
Но значительное улучшение качества модели происходит, если координаты преобразовать в матрицу расстояний между скважинами.
Таким образом, мы даем возможность алгоритму сразу распознать, что близлежащие скважины имеют больший вес, чем удаленные.
Особенности проектирования
Рассчитываем матрицу евклидовых расстояний между скважинами по их координатам.
distance = pd.DataFrame(euclidean_distances(df[['x', 'y']]))
distance
Получение списка названий скважин.
Мы присваиваем названия скважин столбцам матрицы расстояний.
well_names = df['Well']
distance.columns = well_names
Мы объединяем набор данных параметров работы скважин с матрицей расстояний между скважинами.
Таким образом, мы добавляем в набор данных новый признак — расстояние, которое представляет собой вес скважин друг над другом.
df_distance = pd.concat([df.drop(['x', 'y'], axis=1), distance], axis=1)
df_distance

Проверка модели
Из-за небольшого объема данных мы будем тестировать модель методом слепого тестирования.Создаем обучающий набор данных, удаляя из него выбранные для тестирования и прогнозирования скважины.
df_train_1 = df_distance.drop([12, 13, 14, 15], axis=0)
df_train_1
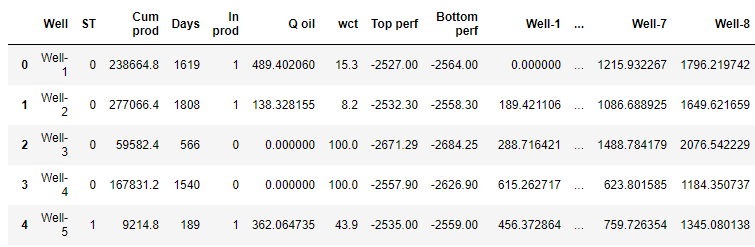
Создание тестового набора данных df_test_1 = df_distance.loc[[12, 13]]
df_test_1

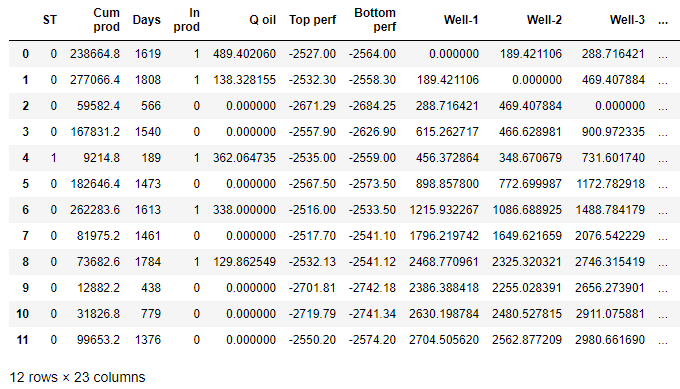
Мы создаем обучающий DataFrame для функций X_1. Мы удаляем категориальный атрибут (имя скважины) и прогнозируемое значение wct. x_1 = df_train_1.drop(['Well', 'wct'], axis=1)
x_1
Создайте обучающий вектор целевых значений y_1 y_1 = df_train_1['wct']
Создайте тестовый вектор целевых значений y_ тест_ 1 y_test_1 = df_test_1['wct']
В качестве алгоритма был выбран обычный Random Forest Regressor, как наиболее универсальный алгоритм, подходящий для большинства типов данных.
x_test_1 = df_test_1.drop(['Well', 'wct'], axis=1)
model = RandomForestRegressor(random_state=42, max_depth=14)
model.fit(x_1, y_1)
y_pred_train_1 = model.predict(x_1)
y_pred_1 = model.predict(x_test_1)
print('Predicted values from train data:')
r2_train = r2(y_1, y_pred_train_1)
mae_train = mae(y_1, y_pred_train_1)
mse_train = mse(y_1, y_pred_train_1)
print(f'R2 train: {r2_train.round(4)}')
print(f'MAE train: {mae_train.round(4)}')
print(f'MSE train: {mse_train.round(4)}')
print('Predicted values from test data:')
r2_test = r2(y_test_1, y_pred_1)
mae_test = mae(y_test_1, y_pred_1)
mse_test = mse(y_test_1, y_pred_1)
print(f'R2 test: {r2_test.round(4)}')
print(f'MAE test: {mae_test.round(4)}')
print(f'MSE test: {mse_test.round(4)}')
model
Predicted values from train data:
R2 train: 0.8832
MAE train: 8.2855
MSE train: 131.1208
Predicted values from test data:
R2 test: 0.8758
MAE test: 3.164
MSE test: 11.4485
RandomForestRegressor(max_depth=14, random_state=42)
Метрика R2 в метрике обучения превышает R2 в метрике теста на 1%.
Это значит, что модель прошла обучение отлично.
Сравним прогнозируемую обводненность с фактической на тестовой выборке, которая не использовалась при обучении модели (слепой тест).
df_y_test = pd.DataFrame({'Well': df_test_1['Well'],
'wct predicted, %': y_pred_1.round(1),
'wct actual, %': y_test_1.round(1),
'difference': (y_pred_1 - y_test_1).
round(1)})
df_y_test

Сравним прогнозируемую обводненность с фактической на обучающей выборке.
df_y_train = pd.DataFrame({'Well': df_train_1['Well'],
'wct predicted, %': y_pred_train_1.round(1),
'wct actual, %': y_1.round(1),
'difference': (y_pred_train_1 - y_1).
round(1)})
df_y_train
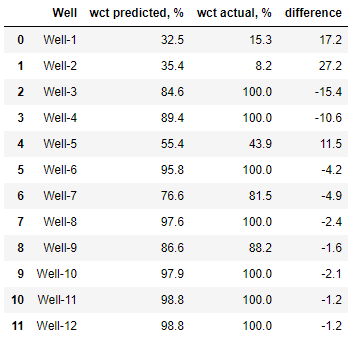
Рассчитаем среднее отклонение обводненности: round(sum(abs(y_pred_train_1 - y_1)) / len(y_1), 1)
8.3 Мы видим, что среднее отклонение по обводненности составляет 8%, что является приемлемым результатом.
Создание модели на всех доступных данных
Создаем обучающий набор данных, удаляя из него выбранные для прогнозирования скважины.
df_train_2 = df_distance.drop([14, 15], axis=0)
Мы создаем набор прогнозных данных из скважин, удаленных на предыдущем шаге.
Прогнозируемый параметр WCT (обводненность) теперь равен NaN. df_fc = df_distance.loc[[14, 15]]
Создайте обучающий DataFrame с функциями x_2. Мы удаляем категориальный атрибут (имя скважины) и прогнозируемое значение wct. x_2 = df_train_2.drop(['Well', 'wct'], axis=1)
Создаем обучающий вектор целевых значений y_2 и обучаем модель.
y_2 = df_train_2['wct']
x_fc = df_fc.drop(['Well', 'wct'], axis=1)
model = RandomForestRegressor(random_state=42, max_depth=14)
model.fit(x_2, y_2)
y_pred_train_2 = model.predict(x_2)
y_fc = model.predict(x_fc)
print('Predicted values from train data:')
r2_train = r2(y_2, y_pred_train_2)
mae_train = mae(y_2, y_pred_train_2)
mse_train = mse(y_2, y_pred_train_2)
print(f'R2 train: {r2_train.round(4)}')
print(f'MAE train: {mae_train.round(4)}')
print(f'MSE train: {mse_train.round(4)}')
print('Forecasted values could be compared with real data!')
model
Predicted values from train data:
R2 train: 0.9095
MAE train: 6.5196
MSE train: 89.9625
RandomForestRegressor(max_depth=14, random_state=42)
R2 увеличился.
Либо модель была перетренирована, либо больше данных помогло более точно настроить модель.
Сравним прогнозируемую обводненность с фактической на обучающей выборке.
df_y_train = pd.DataFrame({'Well': df_train_2['Well'],
'wct predicted, %': y_pred_train_2.round(1),
'wct actual, %': y_2.round(1),
'difference': (y_pred_train_2 - y_2).
round(1)})
df_y_train
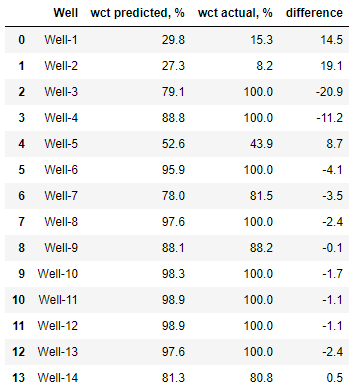
round(sum(abs(y_pred_train_2 - y_2)) / len(y_2), 1)
6,5 Средняя ошибка обводненности снизилась до 6,5. Большой! Прогнозируем обводненность по боковым стволам: df_y_test = pd.DataFrame({'Well': df_test_1['Well'],
'wct predicted, %': y_pred_1.round(1),
'wct actual, %': y_test_1.round(1),
'difference': (y_pred_1 - y_test_1).
round(1)})
df_y_test

Выводим список признаков в порядке убывания их важности и строим диаграмму важности признаков.
model.feature_importances_
feature_importances = pd.DataFrame()
feature_importances['feature_name'] = x_2.columns.tolist()
feature_importances['importance'] = model.feature_importances_
feature_importances = feature_importances.sort_values(by='importance', ascending=False)
feature_importances
fig = px.bar(feature_importances,
x=feature_importances['importance'],
y=feature_importances['feature_name'],
title="Важность функций")
fig.update_layout(yaxis={'categoryorder':'total ascending'})
fig.show()
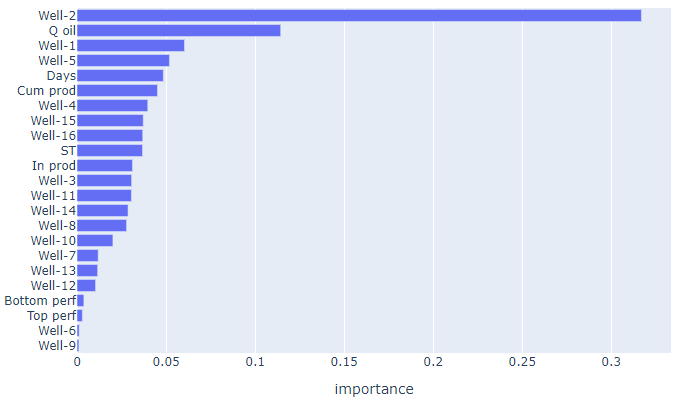
Мы видим, что самая важная особенность – это расстояние до 2-й скважины.
Возможно, стоит проанализировать признаки дальше и исключить некоторые из них из обучения.
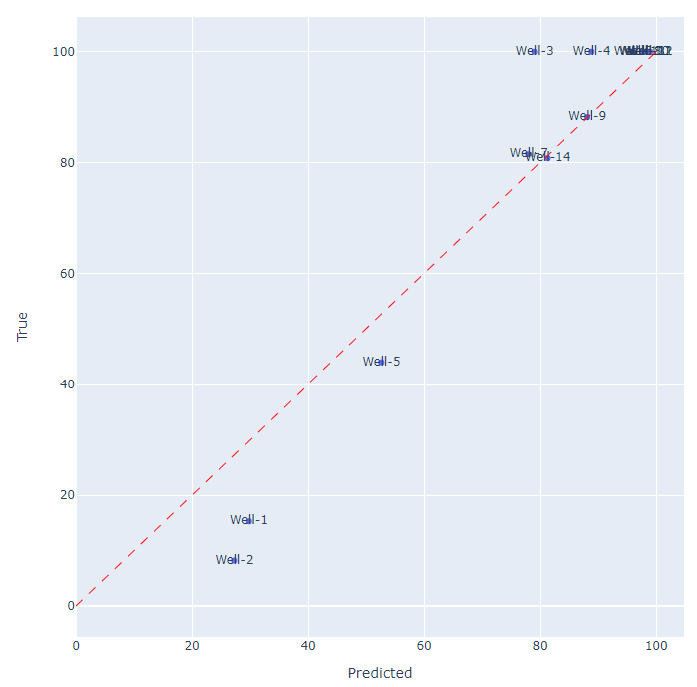
Сравнительный график фактических и прогнозируемых значений.
Чем дальше скважина находится от красной линии, тем хуже она прогнозируется.
fig = px.scatter(x=y_pred_train_2, y=y_2, title="Истинные и прогнозируемые значения",
text=df_train_2['Well'], width=850, height=800)
fig.add_trace(go.Scatter(x=[0,100], y=[0,100], mode='lines', name='True=Predicted',
line = dict(color='red', width=1, dash='dash')))
fig.update_xaxes(title_text='Predicted')
fig.update_yaxes(title_text='True')
fig.show()
Заключение
Прогнозирование параметров работы скважин возможно различными методами.Некоторые из них очень сложны и трудоемки (геолого-гидродинамические модели), другие просты и быстры (матбаланс, кривые падения добычи).
Данный пример построения модели и сравнения прогноза с реальными данными позволяет сделать вывод, что даже очень простая модель «без наворотов» хорошо предсказывает рабочие параметры скважины.
Это означает, что в набор инженера-разработчика нефтяных и газовых месторождений добавляется еще один метод выполнения рабочих задач, который также позволяет решить задачу в очень сжатые сроки.
Примечания
- Эта модель имеет важное ограничение.
Любое месторождение имеет нефтеносный контур – участок, за которым пробуренная скважина будет «сухой» – нефти там нет.
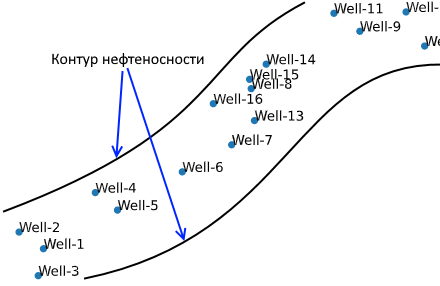
Эта модель слабо чувствительна к местоположению.
Модель «не знает», что за пределами определенной зоны нефти нет. Для решения этой проблемы можно найти и скачать данные о «сухих» скважинах, пробуренных в окрестностях и не обнаруживших нефти.
Также возможно создание искусственных данных по нефтеносному контуру при нулевых дебитах нефти.
В этом примере я не использовал ни один из методов, чтобы не усложнять модель.
- Целью исследования было оценить применимость методов машинного обучения в этой области.
Задача выбора лучшего алгоритма не ставилась, поэтому сравнения разных алгоритмов не проводились.
- Данные скважины не являются общедоступными данными, а являются собственностью компании, владеющей лицензией на разработку месторождения.
Поэтому для иллюстрации проделанной работы мы сгенерировали данные искусственной скважины которые доступны для этой работы.
- Источник вместе с текстом статьи доступен здесь: https://github.com/alex-kalinichenko/re/tree/master/wct_fc

-
Инопланетные Злоумышленники!
19 Oct, 24 -
Интересный Баг Google Earth
19 Oct, 24


