Распространенная аналогия для объяснения градиентный спуск вот так: человек застрял в горах во время сильного тумана и должен спуститься вниз.
Самый логичный способ — сканировать поверхность вокруг себя и медленно спускаться по склону.
В этом суть градиентного спуска, но аналогия всегда разваливается, когда мы переходим в пространство более высоких измерений, о реальной геометрии которого мы мало что знаем.
Хотя обычно это не становится проблемой, поскольку градиентный спуск работает вполне нормально.
Но вот важный вопрос: насколько хорошо работает градиентный спуск на реальной Земле? Определение весов и функций стоимости В общей модели градиентный спуск выбирает веса для модели, которые минимизируют функцию стоимости.
Обычно это некоторое представление ошибок, допущенных моделью в ряде прогнозов.
Но здесь мы ничего не прогнозируем, поэтому «ошибок» у нас нет, поэтому адаптация к наземным путешествиям требует немного расширения контекста обычного машинного обучения.
В нашем алгоритме путешествия по Земле цель состоит в том, чтобы достичь уровня моря из любой начальной позиции.
То есть мы определяем «веса» как широту и долготу, а «функцию стоимости» как текущую высоту.
Другими словами, градиентный спуск должен оптимизировать значения широты и долготы таким образом, чтобы минимизировать высоту над уровнем моря.
К сожалению, у нас нет математической функции для всей земной поверхности, поэтому значения стоимости будем рассчитывать с помощью растра набор данных о высоте от НАСА:
Градиентный спуск учитывает градиент функции стоимости по отношению к каждой переменной, для которой проводится оптимизация.import rasterio # Open the elevation dataset src = rasterio.open(sys.argv[1]) band = src.read(1) # Fetch the elevation def get_elevation(lat, lon): vals = src.index(lon, lat) return band[vals] # Calculate our 'cost function' def compute_cost(theta): lat, lon = theta[0], theta[1] J = get_elevation(lat, lon) return J
Он корректирует переменные так, чтобы они уменьшали функцию стоимости.
Это легко, если ваша функция стоимости является математической метрикой, такой как среднеквадратическая ошибка.
Но, как мы уже упоминали, наша «функция стоимости» представляет собой поиск в базе данных, поэтому нет ничего, из чего можно было бы извлечь.

К счастью, градиент можно аппроксимировать так же, как путешественника в нашей аналогии: осмотревшись вокруг.
Градиент эквивалентен наклону, поэтому давайте оценим наклон, взяв точку немного выше текущего местоположения и точку немного ниже него (в каждом измерении) и разделив их, чтобы получить расчетную производную.
Это должно работать очень хорошо: def gradient_descent(theta, alpha, gamma, num_iters):
J_history = np.zeros(shape=(num_iters, 3))
velocity = [ 0, 0 ]
for i in range(num_iters):
cost = compute_cost(theta)
# Fetch elevations at offsets in each dimension
elev1 = get_elevation(theta[0] + 0.001, theta[1])
elev2 = get_elevation(theta[0] - 0.001, theta[1])
elev3 = get_elevation(theta[0], theta[1] + 0.001)
elev4 = get_elevation(theta[0], theta[1] - 0.001)
J_history[i] = [ cost, theta[0], theta[1] ]
if cost <= 0: return theta, J_history
# Calculate slope
lat_slope = elev1 / elev2 - 1
lon_slope = elev3 / elev4 - 1
# Update variables
theta[0][0] = theta[0][0] - lat_slope
theta[1][0] = theta[1][0] - lon_slope
return theta, J_history
Большой! Обратите внимание, что эта функция отличается от большинства реализаций градиентного спуска тем, что ей не передаются переменные X или Y. Наша функция стоимости не требует расчета ошибки каких-либо прогнозов, поэтому нам нужны только те переменные, которые мы здесь оптимизируем.
Давайте запустим это гора Олимп в Вашингтоне: 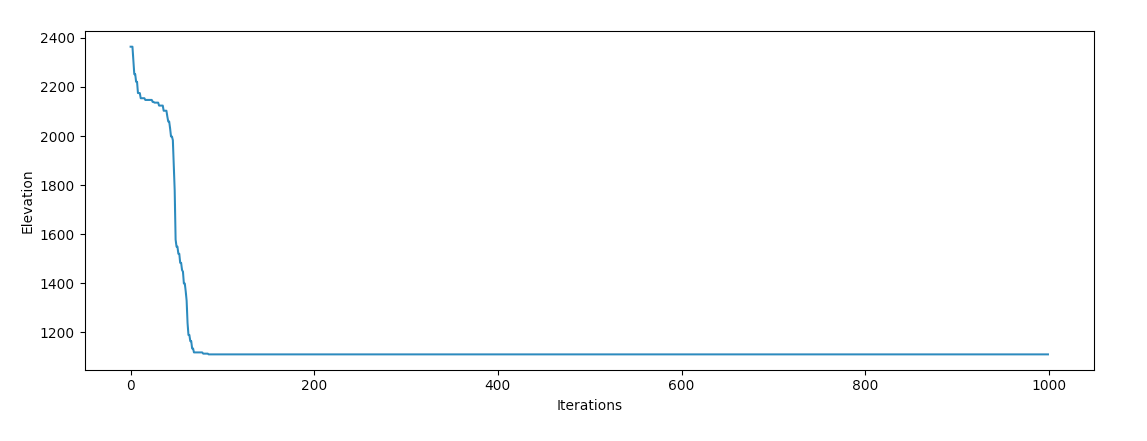
Хм, похоже, он застрял! То же самое происходит при тестировании в большинстве других мест. Оказывается, наша Земля переполненный локальные минимумы, а градиентный спуск испытывает огромные трудности с поиском глобального минимума, если он запущен из локального региона, даже близко к океану.
Оптимизация по инерции Стандартный градиентный спуск — не единственный инструмент, поэтому давайте попробуем его.
оптимизация по инерции (оптимизация импульса).
Инерция основана на реальной физике, поэтому применение ее к градиентному спуску в реальной геометрии — привлекательная идея.
К сожалению, если разместить на вершине Олимпа даже очень большой валун и отпустить его, то вряд ли ему хватит инерции, чтобы скатиться к океану, поэтому придется использовать какие-то нереальные (в физическом смысле) значения гаммы.
здесь: def gradient_descent(theta, alpha, gamma, num_iters):
J_history = np.zeros(shape=(num_iters, 3))
velocity = [ 0, 0 ]
for i in range(num_iters):
cost = compute_cost(theta)
# Fetch elevations at offsets in each dimension
elev1 = get_elevation(theta[0] + 0.001, theta[1])
elev2 = get_elevation(theta[0] - 0.001, theta[1])
elev3 = get_elevation(theta[0], theta[1] + 0.001)
elev4 = get_elevation(theta[0], theta[1] - 0.001)
J_history[i] = [ cost, theta[0], theta[1] ]
if cost <= 0: return theta, J_history
# Calculate slope
lat_slope = elev1 / elev2 - 1
lon_slope = elev3 / elev4 - 1
# Calculate update with momentum
velocity[0] = gamma * velocity[0] + alpha * lat_slope
velocity[1] = gamma * velocity[1] + alpha * lon_slope
# Update variables
theta[0][0] = theta[0][0] - velocity[0]
theta[1][0] = theta[1][0] - velocity[1]
return theta, J_history
После некоторой настройки переменных градиентный спуск должен иметь больше шансов найти океан: 
Успех! Интересно наблюдать за поведением оптимизатора.
Похоже, что он упал в долину и во время спуска «перекатился» из одной стороны в другую, что согласуется с нашим представлением о том, как объект с чрезвычайно высокой инерцией должен вести себя в реальном мире.
Последние мысли На самом деле Земля должна быть Очень простая функция для оптимизации.
Поскольку большая часть территории покрыта океанами, более двух третей возможных входных значений для этой функции возвращают оптимальное значение функции стоимости.
Но наша планета страдает от локальных минимумов и невыпуклой географии.
Я думаю, что именно поэтому это предоставляет много интересных возможностей для изучения того, как методы оптимизации машинного обучения работают с осязаемыми и понятными локальными геометриями.
Похоже, на Олимпе они неплохо поработали, так что давайте считать обычную аналогию, объясняющую градиентный спуск, «подтверждённой»! Если у вас есть какие-либо мысли по этому поводу, пожалуйста, дайте мне знать.
Теги: #Машинное обучение #Алгоритмы #Работа с 3D-графикой #градиентный спуск #инерция #оптимизация импульса #алгоритмы оптимизации

-
Internet Explorer Для Xbox
19 Oct, 24 -
Новый Вид Спама – Спам От Антиспамеров
19 Oct, 24 -
Reactjs + Mobx — Опыт Использования Di
19 Oct, 24 -
«Год Молодежи». Авторы В Студии.
19 Oct, 24


