1. Введение В этой статье представлено применение квантового алгоритма Гровера для решения задачи поиска гамильтоновых циклов в графе.
Сразу хочу отметить, что данное решение проблемы носит обучающий характер.
Это не даст так называемого «квантового превосходства», так как по мере увеличения количества вершин в графе нам потребуется большее количество кубитов, циклов Гровера и запусков самого алгоритма.
Однако я думаю, что этот вариант заслуживает внимания, возможно, кого-то он вдохновит на поиск более оптимального решения.
2. Постановка задачи
Представим, что имеется граф, состоящий из пяти вершин.О , А , Б , С , Д , и восемь ребер.
Вершина О мы будем считать отправной точкой.
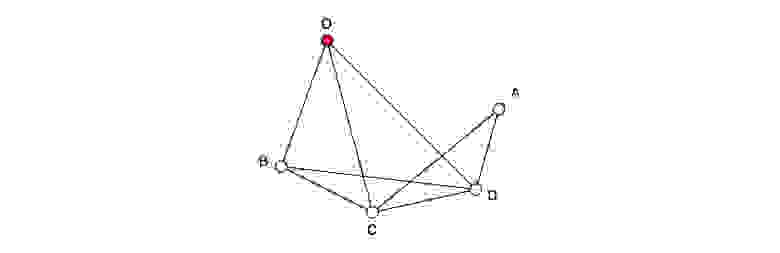
5-вершинный граф Некий путешественник, находящийся в какой-то точке О , хочет пройти все вершины графа, войти в каждую из них только один раз и снова вернуться в исходную точку О .
Необходимо найти все возможные маршруты передвижения, удовлетворяющие условиям задачи.
Решение этой проблемы легко найти самостоятельно.
Всего существует 4 варианта этого пути, несмотря на то, что два из них являются обратными последовательностями двух других:
- ОКАДБО и ОБДАКО

Гамильтоновы циклы в графе (1)
- ОДАКБО и ОБКАДО
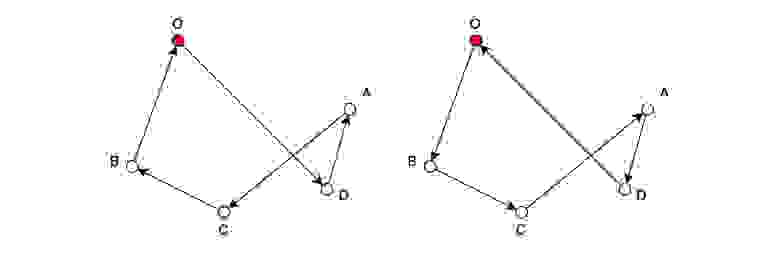
Гамильтоновы циклы в графе (2) Путешественнику в отправной точке О , вам нужно сделать 5 шагов.
На каждом шаге путешественник движется по соединительному ребру от одной вершины к другой.
Все посещенные вершины должны быть уникальными для маршрута, за исключением точки О , путник попадает в нее дважды, так как последний 5-й шаг должен привести его в исходное положение.
Маршрутом будем называть последовательность вершин, через которые должен пройти путешественник, например: ОБКАДО .
Каким бы ни был маршрут (последовательность вершин), он должен удовлетворять следующим правилам:
- вершины маршрута должны быть уникальными, путешественник не заходит в одну и ту же точку дважды;
- Переход на любом шаге маршрута возможен только в ту вершину, которая соединена с текущей:
- А соединяется с С И Д
- Б соединяется с О , С И Д
- С соединяется с О , А , Б , С , Д
- Д соединяется с О , А , Б , С , Д
- маршрут начинается и заканчивается в точке О , поэтому для простоты исключим ее из маршрута, оставив только меняющуюся часть — 4 вершины.
Итак, мы будем перебирать 4 * 4 * 4 * 4 = 256 комбинаций вершин:
При поиске нам необходимо определить, удовлетворяет ли рассматриваемый маршрут в конкретный момент условиям задачи.
Давайте посмотрим на несколько примеров.
Допустим, мы рассматриваем маршрут АДЦБ .
Для путешественника это невозможно, так как первый шаг должен быть из точки О к одной из вершин, соединенных с этой точкой.
Вертекс А не подключается к точке О , нам следует отказаться от такого маршрута.
Другой пример, маршрут СААБ - его тоже нужно выбросить, так как в нем путешественнику придется дважды подняться на вершину А .
Другой пример, маршрут БАКД , его тоже отбрасываем, путешественнику не выбраться из топа Б прямо наверх А (второй шаг), так как эти вершины не связаны.
Итак, нам нужно перебрать 256 комбинаций, из которых следует отбросить те, в которых:
- хотя бы одна из вершин повторяется
- любые две соседние вершины в комбинации не соединены ребром
- первая вершина в комбинации не соединена с начальной точкой О
- последняя вершина в комбинации не соединена с начальной точкой О
Для этого воспользуемся квантовым алгоритмом Гровера.
Давайте выразим маршрут и вершины на языке кубитов.
Возьмем 8 кубитов и разделим их на 4 пары.
Первая пара соответствует первой вершине пути, вторая пара — второй вершине и т. д. В каждой паре кубитов возможна одна из 4-х комбинаций кубитов: 00, 01, 10, 11. Предположим, что каждая из этих комбинаций соответствует одна из возможных вершин: А , Б , С , Д :
Ранее обсуждавшиеся комбинации АДЦБ , СААБ И БАКД будет соответствовать следующим комбинациям кубитов: 00111001, 10000001 и 01001011 соответственно.
Если применить к этим восьми кубитам оператор Адамара, то мы получим суперпозицию всех возможных вариантов движения путешественника, то есть всех 256 комбинаций.
Далее в оракуле нам необходимо реализовать процедуры, которые будут проверять эти комбинации на соответствие условиям задачи.
Однако еще до реализации оракула мы можем использовать один трюк, который позволит нам сократить количество комбинаций почти вдвое.
3. Суперпозиция
Самым первым шагом большинства квантовых алгоритмов является создание суперпозиции всех входных кубитов.Однако здесь мы можем отступить от традиции и использовать небольшую хитрость, которую применили авторы.
Суть трюка в следующем: если мы знаем невозможные комбинации кубитов, мы можем заранее исключить их из суперпозиции.
Так как 1-й шаг делается из точки О , и первая вершина должна быть соединена с этой точкой, а значит, она не может быть вершиной А , это могут быть только вершины Б , С или Д .
Аналогично делается последний 5-й шаг от 4-й вершины до точки О , и он должен быть соединен с точкой О , что означает, что это не может быть вершиной А .
Поскольку первой вершиной маршрута может быть только вершина Б , С или Д , то первая пара кубитов, соответствующая первой вершине маршрута путешественника, может принимать только следующие значения: 01, 10 и 11. То же самое справедливо и для последней пары кубитов, соответствующей четвертой вершине маршрута.
.
Таким образом мы исключим ненужную комбинацию 00 (вершина А ) для первой и четвертой вершин и благодаря этому нам больше не нужно проверять в оракуле связь этих вершин с точкой О , и сократим количество комбинаций до 3*4*4*3 = 144. Итак, давайте посмотрим, как эта техника работает для пары кубитов.
Начальное состояние системы двух кубитов запишем следующим образом:
Выполним ряд преобразований.
Шаг 1. Подействуем на первый кубит оператором
с этим углом
, в котором операторная матрица принимает следующий вид:
Мы не пойдем за угол
ищем «красивое» значение, установим его равным:
Посмотрим, как этот оператор повлияет на первый кубит
:
После того, как оператор воздействует на первый кубит пары, мы получаем следующую суперпозицию двух кубитов:
Шаг 2. Подействуем на второй кубит управляемым вентилем Адамара Управляемый вентиль Адамара изменяет второй кубит только тогда, когда первый кубит равен
Шаг 3. Подействуем на второй кубит гейтом НЕТ Примените гейт ко второму кубиту НЕТ :
Итак, мы имеем суперпозицию, в которой отсутствует комбинация 00. После того как мы подробно рассмотрели теоретическую часть, приступим к написанию соответствующей процедуры.
Библиотека кискит имеет в своем арсенале все клапаны, приведенные в теоретической части:
- Однокубитный вентиль
- Квантовая схема.рай (тета, целевой_кубит)
- тэта - угол
- целевой_кубит — кубит, на который действует ворота
- тэта - угол
- Управляемый вентиль Адамара — QuantumCirquit. ч (control_qubit, target_qubit)
- control_qubit — управляющий кубит
- целевой_кубит — кубит, на который действует ворота
- Однокубитный вентиль НЕТ - Квантовая схема.
Икс (target_qubit)
- целевой_кубит — кубит, на который действует ворота
Сразу отмечу, что должна быть возможность выполнить эту процедуру в обратном порядке, поэтому мы ввели дополнительный аргумент обеспечить регресс .import numpy as np theta = 2 * np.arccos(1 / np.sqrt(3)) def exclude_00(qc, pair, reverse=False): if not reverse: qc.ry(theta, pair[0]) qc.ch(pair[0], pair[1]) qc.x(pair[1]) else: qc.x(pair[1]) qc.ch(pair[0], pair[1]) qc.ry(-theta, pair[0])
О необходимости этого я расскажу позже.
Исключить возможность получения опциона А мы будем с первой и четвёртой вершин маршрута.
Вторая и третья вершины должны иметь все возможные варианты в суперпозиции, поэтому действовать на них будем классически — вентилем Адамара.
4. Оракул
В алгоритме Гровера оракул должен инвертировать фазу «хорошей» комбинации входящих кубитов.Если комбинация удовлетворяет условиям единственности и требованию связности вершин, то оракул должен изменить фазу такой комбинации.
В противном случае, если хотя бы одно из условий нарушено, оракул оставляет фазу неизменной.
Фазовая инверсия эквивалентна простой инверсии полученного кубита из
В
, который не является частью маршрута входного кубита.
Оракул должен быть построен таким образом, чтобы при «хорошей» комбинации результирующий кубит менял свое состояние.
за условие
.
По умолчанию комбинация объявляется «хорошей».
Однако если будет найдена хотя бы одна совпадающая вершина или один несвязный переход между ними, маршрут будет считаться «плохим» и полученный кубит не будет инвертирован.
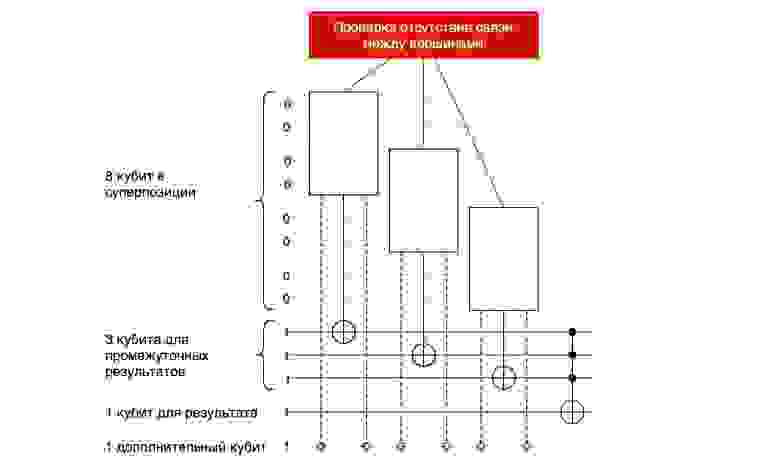
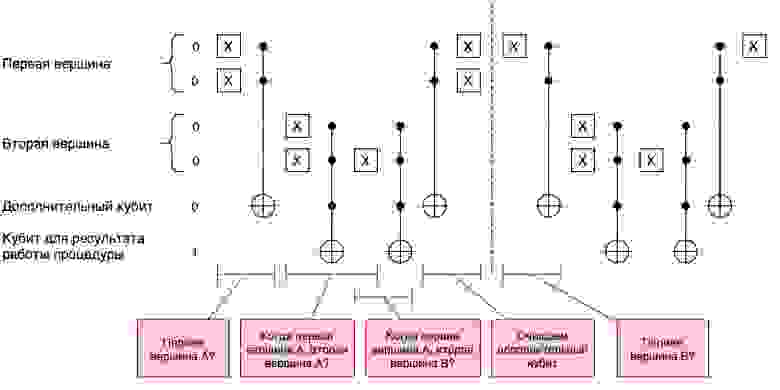
На рисунке примерно показана схема алгоритма решения нашей задачи.

Рассмотрим подробно содержание проверок на уникальность и связность вершин.
4.1. Контроль соответствия вершин
Задача этого блока — не дать оракулу инвертировать полученный кубит, если в комбинации вдруг появятся хотя бы две одинаковые вершины.Чтобы проверить, есть ли в комбинации совпадающие вершины, нам нужно последовательно проверить все возможные пары вершин на равенство.
Для каждой пары вершин мы проверим, являются ли они обеими вершинами одновременно.
А , или Б , или С , или Д .
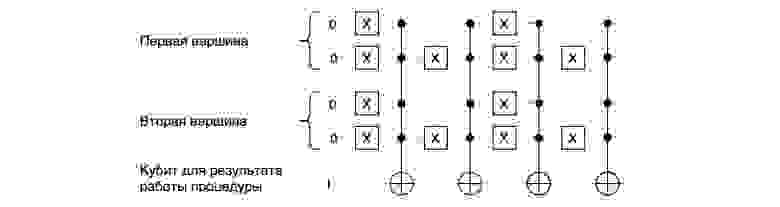
Проверка совпадения вершин Представим, что на вход даны две вершины.
А , то все четыре входных кубита равны 0. После применения вентиля ко всем четырем кубитам НЕТ они становятся равными 1. Множественный вентиль Тоффоли инвертирует полученный кубит. Далее в схеме кубиты будут подвергаться преобразованию для проверки одновременного равенства вершин.
Б , С И Д .
Эти проверки завершатся неудачно и не изменят результирующий кубит; его значение останется инвертированным.
Если на вход подаются несовпадающие вершины, то результирующий кубит останется нетронутым на всех этапах схемы.
Процедура сопоставления вершин Напишем простую процедуру, на входе которой будут две пары кубитов, соответствующих двум вершинам маршрута, а также кубит, в который функция будет передавать результат проверки.
Если одинаковые вершины передаются парами, то процедура меняет полученный кубит на противоположный, сигнализируя о совпадении вершин.
def find_equality(qc, pair_1, pair_2, result_qubit):
qc.x(pair_1 + pair_2)
qc.mct(pair_1 + pair_2, result_qubit)
qc.x([pair_1[1], pair_2[1]])
qc.mct(pair_1 + pair_2, result_qubit)
qc.x(pair_1 + pair_2)
qc.mct(pair_1 + pair_2, result_qubit)
qc.x([pair_1[1], pair_2[1]])
qc.mct(pair_1 + pair_2, result_qubit)
Полная схема «детектора совпадений» будет выглядеть примерно так: 
В оракуле нам нужно будет применить эту процедуру ко всем парам вершин, а так как вершин у нас 4, то процедуру придется запустить 6 раз — это количество комбинаций 4 на 2:
Имея восемь вершин, нам уже нужно будет запустить эту функцию для 28 пар вершин.
Именно эта часть алгоритма является узким местом.
4.2. Проверка связности вершин
Задача этого блока оракула — определить для всех трёх пар соседних вершин, есть ли соединяющее их ребро.Если хотя бы одна такая пара не имеет связи, то процедура не позволяет оракулу объявить комбинацию «хорошей» и изменить полученный кубит. Изменив полученный кубит на 0, процедура не позволит оракулу объявить такой маршрут «хорошим».
Общая логика должна быть следующей: результирующий кубит проверки на связность вершин должен измениться (1 → 0), если хотя бы одна пара соседних вершин не соединена ребром.
Как мы решим эту проблему? Допустим, мы проверяем 3-ю и 4-ю вершины маршрута.
И допустим, третья вершина — это вершина А .
Но мы знаем это сверху А ты можешь добраться только до вершины С И Д .
Поэтому сначала нужно проверить, упала ли вершина на 3 шаге.
А , и если да, то проверяем, какая вершина следующая.
Нам необходимо выявить именно отрицательные случаи, когда следующая 4-я вершина не является вершиной.
С, ни один Д , и только в этом случае объявить комбинацию неудачной.
Мы можем проверить это наоборот, если 4-я вершина является вершиной А или Б (логически эквивалентно «ни С, ни один Д "), то считаем текущую комбинацию неудачной.
Такая "обратная" форма нам проще реализовать и уменьшит количество дополнительных кубитов.
Не забываем, что аналогичные проверки нам нужно провести и для всех остальных случаев, когда третья вершина Б , С или Д .
А также для всех возможных пар соседних вершин маршрута.
Приступим к реализации этой процедуры.
На вход мы дадим ему один кубит для результата и две пары кубитов двух вершин.
Первый назовем основным, второй соседним.
Будем последовательно проверять, какая вершина ( А , Б , С или Д ) — главная вершина.
Для этого нам понадобится клапан Тоффоли.
Далее для каждой из возможных ситуаций мы проверим соседнюю вершину, связана ли она с основной вершиной.
Логика процедуры следующая:
- Проверка, является ли главная вершина вершиной А , если это правда, то проверьте:
- Является ли соседняя вершина вершиной А или Б , если true, то инвертировать полученный кубит.
- Проверка, является ли главная вершина вершиной Б , если это правда, то проверьте:
- Является ли соседняя вершина вершиной А или Б , если true, то инвертировать полученный кубит.
- Проверка, является ли главная вершина вершиной С , если это правда, то проверьте:
- Если соседняя вершина какая-либо, то инвертируем полученный кубит (условие всегда выполняется).
- Если соседняя вершина какая-либо, то инвертируем полученный кубит (условие всегда выполняется).
- Проверка, является ли главная вершина вершиной Д , если true, то логика ниже аналогична логике с вершиной С .
Сначала проверяем, является ли главная вершина вершиной А .
Но как мы можем это проверить? Вертекс А в виде кубита имеет представление 00, мы можем применить гейт к обоим кубитам НЕТ , то пара станет равна 11. Далее мы отправляем эту пару в вентиль Тоффоли в качестве управляющего кубита, он инвертирует дополнительный кубит (0 → 1).
Если главная вершина не является вершиной А , то дополнительный кубит останется неизменным.
Если оно равно, то дополнительный кубит будет инвертирован.
Далее нам нужно проверить соседнюю вершину на равенство с вершиной А или Б .
Для этого введем дополнительный кубит для хранения промежуточного результата проверки, применим кратный гейт Тоффоли к двум кубитам проверяемой вершины, а также в качестве управляющего кубита подадим в гейт с результатом дополнительный кубит проверки того, равна ли главная вершина вершине А .
В случае успеха вентиль Тоффоли инвертирует кубит промежуточного результата теста.
Теперь, когда мы закончили с теоретической частью, приступим к написанию процедуры.
Для начала составим общий список вершин, а заодно зафиксируем представления вершин в кубитах: vertex_names = {
'A': '00',
'B': '01',
'C': '10',
'D': '11',
}
Зафиксируем все соединения вершин (кроме точки О ).
connections = {
'A': ['C','D'],
'B': ['C','D'],
'C': ['A','B','D'],
'D': ['A','B','C'],
}
Создадим каталог функции, который при подаче на вход вершины, соответствующей ключу в словаре, будет выдавать на выходе пару кубитов 11. Вместе с воротами Тоффоли этот каталог можно использовать как условный оператор.
vertex_to_11 = {
'A': lambda qc, pair: qc.x(pair),
'B': lambda qc, pair: qc.x(pair[0]),
'C': lambda qc, pair: qc.x(pair[1]),
'D': lambda qc, pair: None,
}
Далее создадим процедуру, которая получает в качестве аргументов две пары кубитов — основную и соседнюю вершину — и проверяет наличие связи между ними.
Также передаем в процедуру полученный кубит, который заранее подготовлен в состоянии
.
def find_disconnection(qc, pair_1, pair_2, ancilla_qubit, result_qubit):
for letter_1 in connections.keys():
vertex_to_find = [x for x in vertex_names.keys() if x not in connections[letter_1]]
if len(vertex_to_find) > 0:
vertex_to_11[letter_1](qc, pair_1)
qc.toffoli(*pair_1, ancilla_qubit)
for letter_2 in vertex_to_find:
vertex_to_11[letter_2](qc, pair_2)
qc.mct([*pair_2, ancilla_qubit], result_qubit)
vertex_to_11[letter_2](qc, pair_2)
qc.toffoli(*pair_1, ancilla_qubit)
vertex_to_11[letter_1](qc, pair_1)
Эта процедура проверяет одну пару соседних вершин на наличие связи между ними.
Если такой связи нет, то он инвертирует полученный кубит (1 → 0) процедуры, что не позволит оракулу объявить эту комбинацию «хорошей».
5. Оператор диффузии
Оператор диффузии Гровера в матричном выражении представляет собой обычную единичную матрицу, все диагональные элементы которой равны -1, за исключением крайнего левого элемента, который равен 1. Оператор инвертирует фазу любого вектора, кроме вектора.
.
Пример действия оператора над вектором
: Пример действия оператора на любом другом векторе:
Нет необходимости «создавать» конфигурацию клапана для оператора диффузии; оно уже разработано.
Для набора н Оператор кубита будет выглядеть так:
Теги: #Квантовые технологии #Алгоритмы #графы #qiskit #Алгоритм Гровера #Гамильтонов цикл

-
Застой В Развитии: Формат Вывода Сообщений
19 Oct, 24 -
Остерегайтесь Фишинга Firstvds
19 Oct, 24 -
В Животном Мире
19 Oct, 24 -
Fathomdb — Новый Стартап От Y Combinator.
19 Oct, 24


