Часть I Часть II Данная статья в основном посвящена приближениям к Золотое сечение .
Рассмотрим алгоритмическое решение задачи №.
38 из книги «Задания для детей от 5 до 15 лет»
Рассчитайте сумму:
(при ошибке не более 1% ответа)
Ниже представлен алгоритм вычисления частичных сумм этого ряда на языке Схема (Лисп) в окружающей среде DrRacket ( Схема позволяет производить расчеты в обыкновенных дробях):
drRacket рассчитал два последних примера с ошибкой#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000)
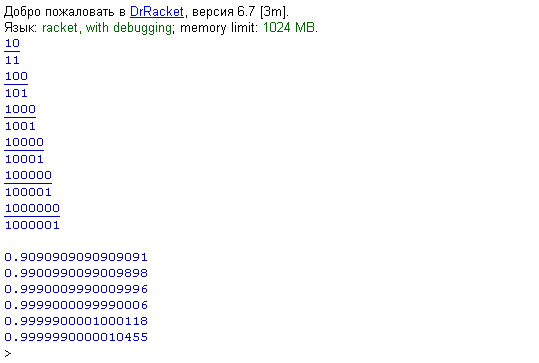
?Эту программу можно запустить в онлайн-режиме ideone.com И codepad.org .
Тот же алгоритм в Python
def series_sum(n):
Теги: #фибоначчи #золотое сечение #непрерывные дроби #приближения #Lisp #python #Занимательные задачи #программирование #математика
Вместе с данным постом часто просматривают:
-
Лазеры Для Повышения Эффективности Двигателя
19 Oct, 24 -
Новый Образовательный Семинар В Киеве
19 Oct, 24


