Всем привет! Новогодние каникулы подошли к концу, а это значит, что мы снова готовы поделиться с вами полезным материалом.
Перевод данной статьи подготовлен в преддверии запуска нового потока на курсе.
«Алгоритмы для разработчиков» .
Идти! 
Обратное распространение ошибки, вероятно, является наиболее фундаментальным компонентом нейронной сети.
Впервые он был описан в 1960-х годах и популяризирован почти 30 лет спустя Румельхартом, Хинтоном и Уильямсом в статье под названием «Изучение представлений с помощью ошибок обратного распространения» .
Метод используется для эффективного обучения нейронной сети с использованием так называемого цепного правила (правила дифференцирования сложной функции).
Проще говоря, после каждого прохода по сети обратное распространение ошибки делает проход в противоположном направлении и корректирует параметры модели (веса и смещения).
В этой статье я хотел бы подробно, с математической точки зрения, рассмотреть процесс обучения и оптимизации простой 4-слойной нейронной сети.
Я считаю, что это поможет читателю понять, как работает обратное распространение ошибки, а также его важность.
Определение модели нейронной сети
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов скрытых слоев и одного нейрона выходного слоя.

Простая иллюстрация четырехслойной нейронной сети.
Входной слой
На рисунке нейроны, выделенные фиолетовым цветом, представляют собой входные данные.Это могут быть простые скалярные величины или более сложные — векторы или многомерные матрицы.

Уравнение, описывающее входные данные xi.
Первый набор активаций (а) равен входным значениям.
«Активация» — значение нейрона после применения функции активации.
Подробности смотрите ниже.
Скрытые слои
Итоговые значения в скрытых нейронах (на рисунке выделены зеленым) рассчитываются с помощью z л – взвешенные входы в слоях I и a я активаций в слое L. Для слоев 2 и 3 уравнения будут следующими: Для l = 2:
Для l = 3:

Вт 2 и Вт 3 — веса на слоях 2 и 3, а b 2 и б 3 – смещения на этих слоях.
Активации 2 и 3 рассчитываются с помощью функции активации f. Например, эта функция f является нелинейной (например, сигмовидная , РеЛУ И гиперболический тангенс ) и позволяет сети изучать сложные закономерности в данных.
Мы не будем вдаваться в подробности того, как работают функции активации, но если вам интересно, очень рекомендую прочитать эту замечательную статья .
Если вы присмотритесь, то увидите, что все x, z 2 ,а 2 , з 3 ,а 3 , Вт 1 , Вт 2 ,б 1 и б 2 не имеют индексов, показанных на рисунке четырехслойной нейронной сети.
Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям.
Это стандартный способ работы с нейронными сетями, и он достаточно удобен.
Однако я пройдусь по уравнениям, чтобы избежать путаницы.
В качестве примера возьмем слой 2 и его параметры.
Те же операции можно применить к любому слою нейронной сети.
Вт 1 представляет собой матрицу весов размерности (н, м) , Где н — количество выходных нейронов (нейронов следующего слоя), а м – количество входных нейронов (нейронов предыдущего слоя).
В нашем случае п=2 И м = 4 .

Здесь первое число в индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущий слой (в нашем случае это входной слой).
Икс – входной вектор с размерностью ( м , 1), где м – количество входных нейронов.
В нашем случае м = 4. 
б 1 – вектор размерного смещения ( н , 1), где н – количество нейронов на текущем слое.
В нашем случае н = 2. 
Следуя уравнению для z 2 мы можем использовать приведенные выше определения W 1 , х и б 1 чтобы получить уравнение z 2 :
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше: 
Как видите, з.
2 может быть выражено через z 1 2 и г 2 2 , где z 1 2 и г 2 2 – сумма произведений каждого входного значения x я соответствующему весу W ij 1 .
Это приводит к тому же уравнению для z 2 и доказывает, что матричные представления z 2 ,а 2 , з 3 и 3 – верны.
Выходной слой
Последняя часть нейронной сети — это выходной слой, который выдает прогнозируемое значение.
В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитанного следующим образом: 
Опять же, мы используем матричное представление, чтобы упростить уравнение.
Вы можете использовать описанные выше методы, чтобы понять основную логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение через нейронную сеть.
Вот краткий обзор: 
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Последним шагом прямого прохода является оценка прогнозируемого выходного значения.
с относительно ожидаемого выходного значения й .
Выходные данные y являются частью набора обучающих данных (x, y), где Икс – входные данные (как мы помним из предыдущего раздела).
Оценка между с И й происходит через функцию потерь.
Это может быть так же просто, как Средняя квадратическая ошибка или более сложный, например перекрестная энтропия .
Мы назовем эту функцию потерь C и обозначим ее следующим образом: 
Где расходы может быть равна среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
На основе значения C модель «знает», насколько ей нужно скорректировать свои параметры, чтобы приблизиться к ожидаемому выходному значению.
й .
Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиента
На основе статьи 1989 года метод обратного распространения ошибки: Постоянно корректирует веса соединений в сети, чтобы минимизировать разницу между фактическим выходным вектором сети и желаемым выходным вектором..
И .
предоставляет возможность создавать новые полезные функции, которые отличают обратное распространение ошибки от более ранних, более простых методов.
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети.
Степень коррекции определяется градиентами функции потерь по этим параметрам.
Возникает один вопрос: Зачем рассчитывать градиенты ? Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые вычислительные концепции: Градиент функции C(x 1 , Икс 2 , …, Икс м ) в точке x называется вектор частных производных От до Икс .

Производная функции C отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента.
Икс ( входное значение ).
Другими словами, производная говорит нам, в каком направлении движется C. Градиент показывает, насколько нужно изменить параметр.
Икс (положительный или отрицательный), чтобы минимизировать C. Эти градиенты рассчитываются с использованием метода, называемого цепочкой.
правило .
За одну гирю (в джк ) л градиент: 
(1) Правило цепочки
(2) По определению m — количество нейронов на l – 1 слое.
(3) Расчет производной
(4) Окончательное значение
Аналогичную систему уравнений можно применить к (b дж ) л : 
(1) Правило цепочки
(2) Расчет производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом: 
«Локальный градиент» можно легко определить с помощью правила цепочки.
Я не буду сейчас описывать этот процесс.
Градиенты позволяют оптимизировать параметры модели:
До достижения критерия остановки выполняются следующие действия: 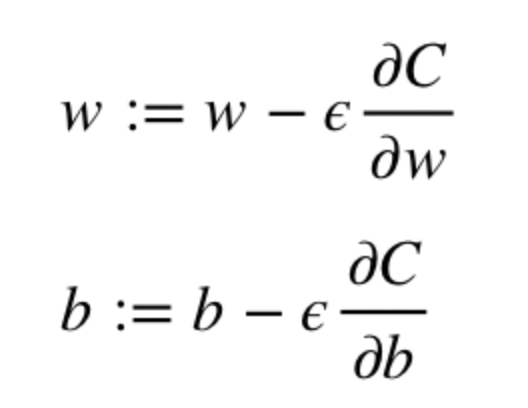
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском) Начальные значения ш И б выбираются случайным образом.
Эpsilon (e) — скорость обучения.
Он определяет эффект градиента.
ш И б – матричные представления весов и смещений.
Производная от C по ш или б может быть рассчитан с использованием частных производных C относительно отдельных весов или смещений.
Условие завершения выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы вычисляем градиент C относительно одного веса (w 22 ) 2 .
Давайте увеличим нижнюю часть приведенной выше нейронной сети: 
Визуальное представление обратного распространения ошибки в нейронной сети
Вес (вес 22 ) 2 соединяет (а 2 ) 2 и (з 2 ) 2 , поэтому для расчета градиента необходимо применить правило цепочки к (z 2 ) 3 и (а 2 ) 3 : 
Расчет конечного значения производной C по (a 2 ) 3 требует знания функции C. Поскольку C зависит от (a 2 ) 3 , вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить свет на математику расчета градиентов.
Если вы хотите узнать больше, я настоятельно рекомендую вам просмотреть серию статей о НЛП в Стэнфорде, где Ричард Сочер дает 4 замечательных объяснения.
обратное распространение ошибки .
Заключительное примечание
В этой статье я подробно объяснил, как работает обратное распространение ошибки, используя математические методы, такие как расчет градиента, цепное правило и т. д. Знание механики этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными модели.Удачи в вашем путешествии по глубокому обучению! Вот и все.
Приглашаем всех на бесплатный вебинар по теме «Дерево сегментов: просто и быстро» .
Теги: #математика #Алгоритмы #Большие данные #наука о данных #искусственный интеллект #глубокое обучение #алгоритмы #Математика

-
Кропоткин Петр Алексеевич
19 Oct, 24 -
Биткаса Стартовала!
19 Oct, 24 -
Рождественские Развлечения С Google Maps
19 Oct, 24 -
Откуда Приходит Внутренний Голос?
19 Oct, 24


