Понимание Теоремы Байеса

Когда вы решаете совершить действие (если, конечно, вы разумный человек), вы делаете ставку на то, что после совершения этого действия оно приведет к лучшему результату, чем если бы этого действия не произошло.

Но ставки - это вещь ненадежный, как ты в конечном итоге решаешь, делать тот или иной шаг или нет? В любом случае вы оцениваете вероятность успешного результата, и если эта вероятность превышает определенный порог, вы делаете шаг.

Поэтому возможность точно оценить вероятность успеха имеет решающее значение для принятия правильных решений.

Хотя случай всегда будет играть роль в конечном результате, вам следует научиться правильно использовать эти шансы и со временем обратить их в свою пользу.

Именно здесь на помощь приходит теорема Байеса — она дает нам количественную основу для сохранения нашей веры в результат действия при изменении факторов окружающей среды, что, в свою очередь, позволяет нам со временем улучшать процесс принятия решений.

Сейчас это кажется порочным кругом, но скоро мы поймем, почему эта формула работает; П(А) – априорная (безусловная) вероятность наступления события А; П(Б) – априорная (безусловная) вероятность наступления события Б.

Допустим, вы недавно прошли курс по анализу данных в учебном лагере.

Вы не получили ответа от некоторых компаний, в которых брали интервью, и начинаете беспокоиться.

Итак, вы хотите посчитать вероятность того, что конкретная компания сделает вам предложение о работе, учитывая, что прошло уже три дня, а вам так и не перезвонили.

Перепишем формулу на примере нашего примера.

В этом случае результат А ( Предложение ) получает предложение о работе, а результат B ( Нет вызова ) – «Три дня не звонил».

Исходя из этого, нашу формулу можно переписать следующим образом: П( Предложение | Нет вызова ) = Р( Нет вызова | Предложение ) * П( Предложение )/П( Нет вызова ) Значение П( Предложение | Нет вызова ) — это вероятность получения предложения при условии отсутствия звонка в течение трех дней.

Эту вероятность чрезвычайно сложно оценить.

Однако обратная вероятность П( Нет вызова | Предложение ) , то есть отсутствие телефонного звонка в течение трех дней, с учетом того, что в итоге вы получили предложение о работе от компании, вполне можно придать некоторый смысл.

Из разговоров с друзьями, рекрутерами и консультантами вы узнаете, что вероятность невелика, но иногда компания все же может хранить молчание в течение трех дней, если все же планирует вас нанять.

Итак, вы оцениваете: П( Нет вызова | Предложение ) = 40% 40% — это неплохо и кажется надежда еще есть! Но мы еще не закончили.

Теперь нам нужно оценить П( Предложение ) , вероятность выхода на работу.

Всем известно, что поиск работы — долгий и трудный процесс, и, возможно, вам придется пройти собеседование несколько раз, прежде чем вы получите это предложение, поэтому оцените: П( Предложение ) = 20% Теперь нам осталось только оценить П( Нет вызова ) , скорее всего, вам не позвонят из компании в течение трех дней.

Есть много причин, по которым вам могут не перезвонить в течение трех дней – возможно, вашу заявку отклонили или все еще проводят собеседование с другими кандидатами, или рекрутер просто болен и поэтому не звонит. Что ж, есть много причин, по которым вам могут не позвонить, поэтому вы оцениваете эту вероятность как: П( Нет вызова ) = 90% Теперь, сложив все это вместе, мы можем вычислить П( Предложение | Нет вызова ) : П( Предложение | Нет вызова ) = 40% * 20%/90% = 8.9% Это совсем немного, поэтому, к сожалению, рациональнее оставить надежду на эту компанию (и продолжать рассылать свое резюме другим).

Если это все еще кажется немного абстрактным, не волнуйтесь.

Я почувствовал то же самое, когда впервые узнал о теореме Байеса.

Теперь давайте посмотрим, как мы пришли к этим 8,9% (имейте в виду, что ваша первоначальная оценка в 20% уже была низкой).

В нашем примере априорную вероятность можно рассматривать как вероятность того, что вы получите предложение о работе в момент выхода из собеседования.

Появляется новая информация - прошло 3 дня, а компания вам так и не перезвонила.

Поэтому мы используем другие части уравнения, чтобы скорректировать нашу априорную вероятность нового события.

Давайте посмотрим на вероятность Р(Б|А) , который в нашем примере называется П( Нет вызова | Предложение ) .

Именно это и делает теорема Байеса.

Давайте переформулируем теорему Байеса в статистических терминах, чтобы сделать ее более понятной (я выучил это отсюда ):



Для меня, например, такая запись выглядит более наглядно.

У нас есть априорная гипотеза (Hypothesis) - что мы получили работу, и наблюдаемые факты - доказательства (Evidence) - три дня нет телефонного звонка.

Теперь мы хотим узнать вероятность того, что наша гипотеза верна с учетом данных фактов.

Как мы решили выше, у нас есть возможность Р(А) = 20% .

Пора перевернуть все с ног на голову! Мы используем П( Доказательство | Гипотеза ) посмотреть на проблему с другой стороны и спросить: «Какова вероятность того, что эти свидетельствующие события произойдут в мире, где наша гипотеза вернаЭ» Итак, возвращаясь к нашему примеру, мы хотим знать, насколько вероятно, что, если нам не позвонят в течение трех дней, нас все равно возьмут на работу.

На изображении выше я отметил П( Доказательство | Гипотеза ) , как и «скалер» (скалер), потому что это слово хорошо отражает суть значения.

Когда мы умножаем его на априорное значение, это уменьшает или увеличивает вероятность события, в зависимости от того, «вредит» ли какое-либо очевидное событие нашей гипотезе.

В нашем случае, чем больше дней пройдет без звонка, тем меньше вероятность, что нас вызовут на работу.

3 дня молчания — это уже плохо (они снижают нашу априорную вероятность на 60%), а 20 дней без звонка полностью уничтожат всякую надежду получить работу.

Таким образом, чем больше событий-доказательств накапливается (больше дней проходит без звонка), тем быстрее масштабатор снижает вероятность.

Скелер — это механизм, который теорема Байеса использует для корректировки наших суждений.

Есть одна вещь, с которой я боролся в оригинальной версии этой статьи.

Это было заявление о том, почему П( Доказательство | Гипотеза ) легче оценить, чем P(гипотеза|доказательства).

Причина этого в том, что П( Доказательство | Гипотеза ) — это гораздо более ограниченная область суждения о мире.

Сужая площадь, мы упрощаем задачу.

Можно провести аналогию с огнем и дымом, где огонь — это наша гипотеза, а наблюдение дыма — событие, доказывающее наличие огня.

P(огонь|дым) Оценить сложнее, поскольку дым может быть вызван многими вещами: выхлопными газами автомобилей, заводами, человеком, жарящим гамбургеры на углях.

В которой P(дым|огонь) легче оценить, потому что в мире, где есть огонь, почти наверняка будет дым.

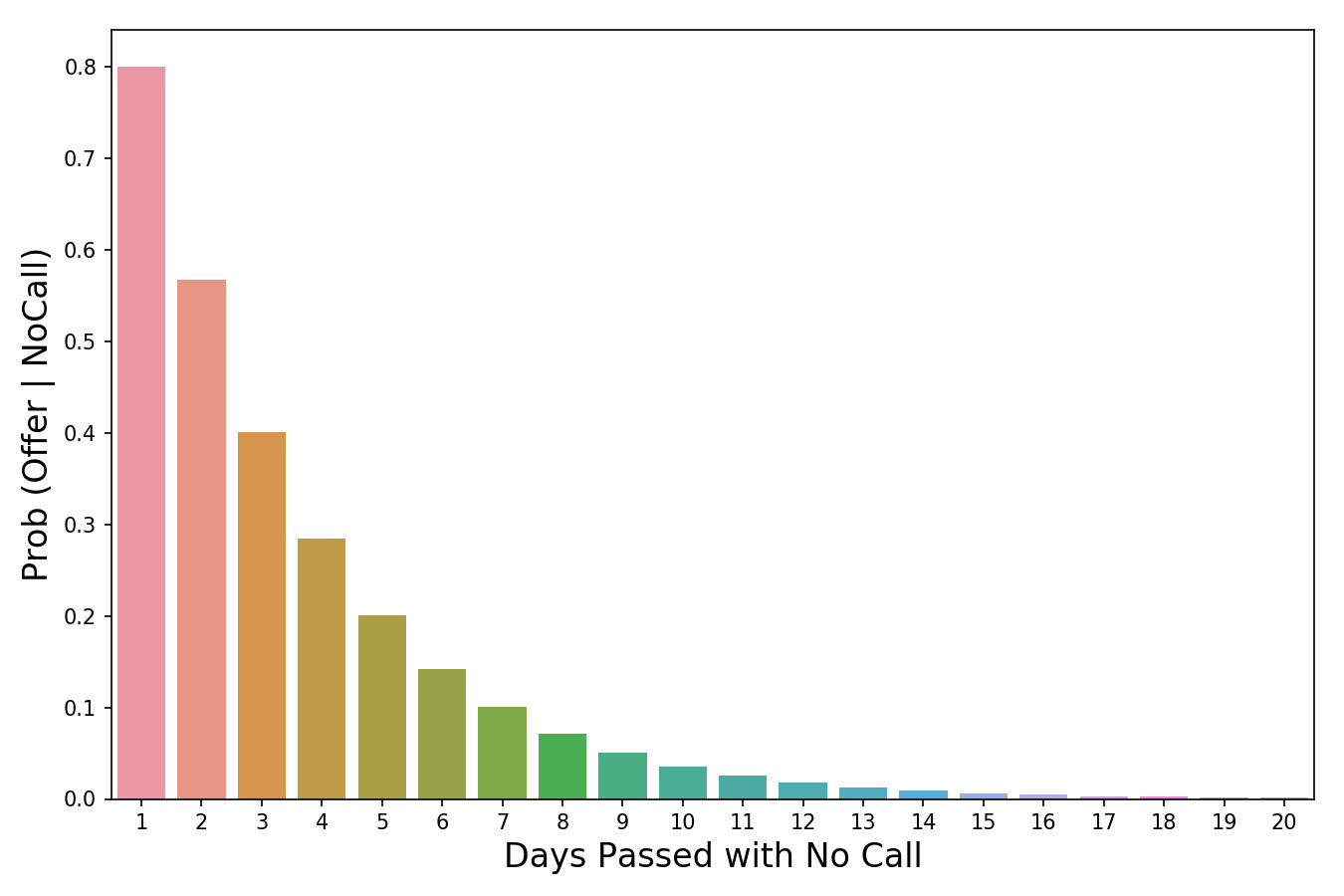
Значение вероятности уменьшается по мере того, как проходят дни без звонка.

Последняя часть формулы, П(Б) или П( Доказательство ) является нормализатором.

Как следует из названия, его цель — нормализовать произведение априорной вероятности и масштабатора.

Если бы у нас не было нормализатора, мы бы имели следующее выражение:



Обратите внимание, что произведение априорной вероятности и масштабатора равно совместной вероятности.

И поскольку один из компонентов в нем П( Доказательство ) , то на совместную вероятность будет влиять малая частота событий.

Это проблема, поскольку совместная вероятность — это величина, включающая все состояния мира.

Но нам не нужны все состояния, нам нужны только те состояния, которые подтверждены доказательными событиями.

Другими словами, мы живем в мире, где события — доказательства — уже произошли, и их количество уже не имеет значения (поэтому мы не хотим, чтобы они в принципе влияли на наши расчеты).

Разделив произведение априорной вероятности и масштабатора на П( Доказательство ) меняет его с совместной вероятности на условную (апостериорную).

Условная вероятность учитывает только те состояния мира, в которых произошло событие доказательства, чего мы и пытаемся достичь.

Другой способ понять, почему мы делим скалер на нормализатор, состоит в том, что они отвечают на два важных вопроса, и их отношения объединяют эту информацию.

Возьмем пример из моего недавнего статьи о Байесе .

Предположим, мы пытаемся выяснить, является ли наблюдаемое животное кошкой, основываясь на одном атрибуте: ловкости.

Все, что мы знаем, это то, что животное, о котором мы говорим, проворное.

Чем больше дней проходит без звонка, тем меньше вероятность, что нас возьмут на работу.

Например, после трех дней без звонка мы считаем, что в мире, где мы можем получить эту работу, существует только 40% вероятность того, что компания будет ждать так долго, прежде чем позвонить вам.

Умножаем масштабатор на априорную вероятность и получаем 20% * 40% = 8%.

Наконец, мы понимаем, что 8% рассчитано для всех состояний, в которых может находиться мир.

Но нас беспокоят только те условия, когда нам не позвонили в течение трех дней.

Чтобы работать только с этими условиями, мы принимаем априорную вероятность того, что звонка не будет в течение трех дней, за 90% и получаем нормализатор.

Делим полученные ранее 8% на нормализатор 8%/90%=8,9% и получаем окончательный ответ. Итак, независимо от ситуации в мире, если вам не позвонили из компании в течение трех дней, ваш шанс получить работу составляет всего 8,9%.