В этом посте я расскажу о том, как можно найти похожие документы, используя MinHash + Locality Sensitive Hashing. Описание LHS и Minhash в Википедии пестрит пугающим количеством формул.
На самом деле это довольно просто.
1. Извлечение признаков
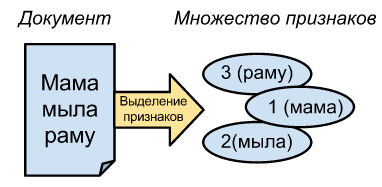
Под документом в этой статье я подразумеваю простой текст, но в целом это может быть любой массив байтов.
Все дело в том, что для сравнения любого документа с помощью MinHash его сначала необходимо преобразовать в набор элементов.
Для текстов хорошей идеей является преобразование в набор идентификаторов слов.
Допустим, «мама постирала раму» -> [1, 2, 3], а «мама постирала раму» -> [1, 2].
Сходство этих наборов составляет 2/3, где 2 — количество похожих элементов, а 3 — общее количество разных слов.
Также можно разбить эти тексты на N-граммы, например, «мама мыла рамку» разбивается на триграммы «мама, ама, ма_, а_м,.
», что даст сходство 7/12.
2. Создание подписи с помощью MinHash
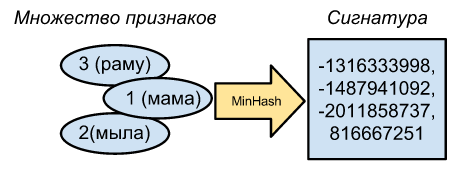
Капитан Очевидность сообщает нам, что MinHash — это минимальный хеш из всех хэшей в нашем наборе.
Скажем, если у нас есть простая случайная хеш-функция f(v) = v, то наши наборы идентификаторов слов [1, 2, 3] и [1, 2] преобразуются в набор хешей [ 1078 , 2573, 7113] и [ 1078 , 2573], и для каждого набора минхеш равен 1078 .
Кажется, это легко.
Вероятность того, что минимальные хеши для двух наборов совпадут, в точности равна сходству двух наборов.
Я не хочу это доказывать, потому что.
у меня аллергия на формулы, а это очень важно.
Ладно, имея один минхеш, мы многого не сделаем, но уже понятно, что одинаковые наборы будут давать один и тот же минхеш, а для совершенно разных наборов и идеальной хеш-функции он гарантированно будет разным.
Для консолидации результата мы можем взять множество разных хэш-функций и найти минхеш для каждой из них.
Получить множество различных хэш-функций довольно легко, сгенерировав множество случайных, но разных чисел, и на основе этих чисел сгенерировать нашу первую хеш-функцию.
Допустим, мы генерируем полностью случайные числа 700 и 7000, что даст нам две дополнительные хэш-функции.
Тогда минхеши для [1, 2, 3] будут (1078, 2573, 7113) -> 1078 , (1674, 2225, 6517) -> 1674 , (8046, 4437, 145) -> 145 , а для [1, 2] минхеши та же сигнатура будет равна (1078, 2573) -> 1078 , (1674, 2225) -> 1674 , (8046, 4437) -> 4437 .
Как видите, первые две пары минхешей совпадают, из чего можно очень грубо предположить, что сходство исходных наборов составляет 2/3. Понятно, что чем больше хеш-функций, тем точнее можно определить сходство исходных наборов.
3. Генерация ключей с помощью локально-зависимого хеширования
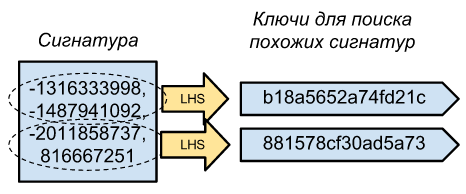
Теперь мы можем определить, насколько похожие документы используют только свои подписи (значения N минхэшей), но что нужно записать в хранилище «ключ-значение», чтобы иметь возможность выбирать все более или менее похожие документы? Если мы будем использовать в качестве ключей целые подписи, то мы будем делать выборку только из практически одинаковых документов, поскольку вероятность совпадения N минхэшей равна s^N, где s — идентичность документов.
Решение простое — допустим, наша подпись состоит из 100 цифр, мы можем разбить ее на несколько частей (скажем, 10 частей по 10 цифр), а затем сделать все эти части ключами всей подписи.
Вот и все, теперь определимся, что подобный документ у нас уже есть в базе.
Вам необходимо получить его подпись из 100 минхэшей, разбить ее на десять ключей и для всех соответствующих им полных подписей вычислить ее сходство (количество совпадающих минхешей).
Для десяти ключей по десять элементов в каждом вероятность выбора документа в зависимости от сходства документа будет следующей: 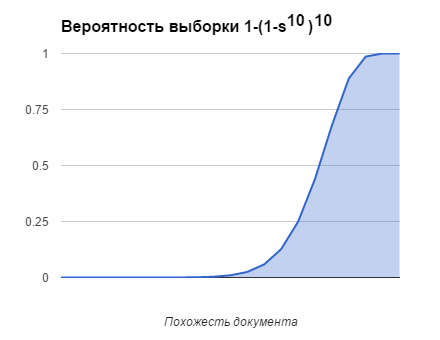
Теги: #minhash #lhs #похожие наборы #jaccard #Интеллектуальный анализ данных #Алгоритмы #Большие данные

-
Опрос По Opera Mini 7 Далее
19 Oct, 24 -
Изменить Размер
19 Oct, 24 -
За Нами Следят Или Кликджекинг Ради Бизнеса
19 Oct, 24


