Есть хорошая статья Питера Норвига, в которой он рассказывает о том, как написать проверку орфографии в 20 строк кода.
В этой статье он показывает, как поисковые системы могут исправлять ошибки в запросах.
И делает это весьма элегантно.
Однако его подход имеет два серьезных недостатка.
Во-первых, исправление более трёх ошибок требует много ресурсов.
А Google, кстати, неплохо справляется с четыре ошибки .
Во-вторых, нет возможности проверить связный текст. 
Итак, я хочу решить эти проблемы.
А именно, написать корректор для коротких фраз или запросов, которые:
- сможет обнаружить три (или более) ошибки в запросе;
- сможет проверять «сломанные» или «слипшиеся» фразы, например expertexchange — expert_exchange, ma na ger — менеджер
- для реализации не потребовалось много кода
- может быть расширен для исправления ошибок на других языках и других типов ошибок
Как определить ошибку
Для начала решим задачу на поиск ошибки в одном слове.Допустим, у нас есть словарь и есть слово, которое нужно проверить.
Мы можем пойти по пути, о котором писал Норвиг:
- найди это слово в словаре
- если нет, сгенерируйте однобуквенные ошибки и проверьте словарь
- в случае неудачи снова сгенерировать двухбуквенные ошибки и снова использовать словарь
Для проверяемого слова создается набор слов, которые получаются с помощью 4 операций: удаления, вставки, замены и перестановки.
Например, ошибки замены «а» на «о» в слове «ашибка» дадут следующие слова: ошибка, аайбка, ашабка, ашиака, ашибаа, ашибка.
Понятно, что это делается для всех букв алфавита.
Аналогичным образом формируются варианты слов для вставки, удаления и перестановки.
У этого подхода есть один недостаток.
Если посчитать, то для английского алфавита и слова длиной в 5 символов получим около 400 вариантов одной ошибки.
За две ошибки – 160 000. За три ошибки – более шести миллионов.
И даже если проверка словаря происходит за константное время, генерация такого количества вариантов занимает слишком много времени.
И это съест много памяти.
Мы можем пойти другим путем: сравнить проверяемое слово с каждым словом в словаре, используя некоторую меру сходства.
Это поможет нам Расстояние Левенштейна .
Короче говоря, расстояние Левенштейна — это минимальное количество правок, которое необходимо применить к первой строке, чтобы получить вторую.
Классическая версия рассматривает три операции: вставку, удаление и замену.
Например, чтобы получить слово «кафе» от слова «кот», нам нужны две операции: одна замена (t-> f) и одна вставка (-> e).
Калифорния т Калифорния фе Но и здесь есть подвох.
Расстояние Левенштейна вычисляется за время O(n*m), где n,m — длины соответствующих строк.
Таким образом, вычислить расстояние Левенштейна в лоб невозможно.
Однако с этим можно работать, преобразуя словарь в конечный автомат.
Конечные автоматы
Да-да, те самые.А они нужны для того, чтобы представить словарь как единую структуру.
Эта структура очень похожа на trie, с небольшими отличиями.
Итак, конечный автомат — это своего рода логическое устройство, которое принимает на вход строку и либо принимает, либо отклоняет ее.
Формально все это можно записать, но я постараюсь обойтись без этого, чтобы вид формул никого не усыпил.
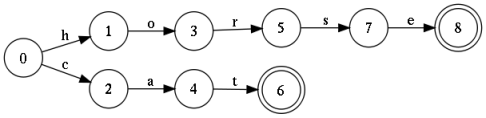
На рисунке изображен автомат, который принимает на вход любую конечную последовательность символов, но допускает только два слова: «кошка» и «лошадь».
Такой автомат называется акцептором.
К этой конструкции легко добавить еще несколько тысяч слов, и в результате получится полноценный словарь.
Стоит отметить, что эту конструкцию можно свернуть и хранить сотни тысяч слов.
Если соблюдать условие детерминированности (дуги, выходящие из любого состояния, не имеют одинаковых меток), то поиск будет осуществляться за линейное время.
И это хорошо.
Но простого акцептора здесь недостаточно.
Вам нужно представить немного более сложную конструкцию, называемую преобразователем конечного состояния или преобразователем.
От акцептора он отличается тем, что каждая дуга имеет два символа: входящий и исходящий.
Это позволяет не только «принять» или «отклонить» строки, но и преобразовать входящую строку.

Вот пример преобразования строки «кошка» в строку «лиса».
Состав игровых автоматов
Конвертер — это математический объект. Как набор, или, лучше сказать, как регулярное выражение.Как и регулярное выражение, преобразователь определяет конкретный язык, то есть набор строк.
Также преобразователи можно скрещивать, комбинировать, инвертировать и т. д. Но в отличие от регулярного выражения, в нем есть очень полезная операция, называемая композицией.
Если описать неформально, то суть операции заключается в следующем.
Проходим одновременно через первый и второй преобразователь, при этом символы на выходе первого «подаются» на вход второго.
Если успешный путь найден как в первом, так и во втором преобразователе, мы записываем его в новый результирующий преобразователь.
Надо сказать, это очень неформальное объяснение.
Однако формализация приведет к необходимости раскатать целый пласт теории, а это не входило в мои планы.
Для официальной информации обращайтесь: Википедия .
Дает строгую формализацию Мехриар Мори .
Он пишет очень интересные статьи на эту тему, хотя и непростые для чтения.
Расстояние Левенштейна через композицию
Пришло время перейти к объяснению, чем это поможет при расчете расстояния Левенштейна.Здесь следует отметить, что преобразователь может содержать специальные символы, обозначающие пустую строку (пустой символ, обозначим его «eps»).
Это позволит нам использовать их в качестве операций редактирования.
Все, что нам нужно, это выполнить композицию из трех преобразователей:
- преобразователь, представляющий первое слово
- преобразователь, представляющий модель ошибки
- преобразователь, представляющий второе слово
рисунки).
Они позволяют слова кот И ванна .


Модель ошибки – это состояние с рефлексивными (замкнутыми на себе) переходами.
Все они, за исключением перехода a:a, представляют собой операции редактирования:
- a:a - оставить символ без изменений
- a:b — замена символов; здесь от «а» до «б»
- eps:a — вставить символ
- a:eps — удалить символьный символ
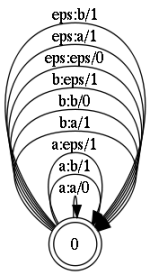
Чтобы не загромождать картинку, на ней показаны исправления только для двух букв.
Здесь следует отметить, что каждый переход отмечен номером.
Это обозначения корректирующих грузов.
Те.
для операций вставки, замены, удаления вес равен 1. Тогда как для перехода типа а:а, который просто переводит исходный символ без исправления, вес равен 0. В результате итоговая композиция примет следующий вид .
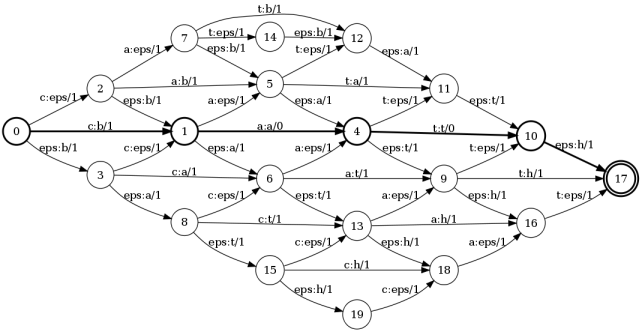
И вот результат: сумма весов по кратчайшему пути есть расстояние Левенштейна .
В этом примере этот путь: 0 — 1 — 4 — 10 — 17 .
Сумма весов на этом пути равна 2. Теперь проследим по меткам на этом пути: c:ba a:a t:t eps:h. Это не что иное, как операции редактирования.
Те.
чтобы получить слово ванна от слова кот нам нужно заменить первую букву и добавить «h» к последней.
Таким образом, мы можем рассчитать расстояние Левенштейна между двумя преобразователями.
Но это означает, что мы можем вычислить это расстояние между строкой и словарем.
Это позволит вычислить ближайшее слово в словаре и дать правильный вариант исправления.
Языковая модель
Как исправить ошибки в отдельных словах, уже понятно.Но как исправить ошибку, когда два слова слиплись.
Например, если вместо Pen Island кто-то напишет penisland. Причем разделять эти слова нужно правильно, чтобы не травмировать нежную психику пользователя.
Кстати, и Яндекс, и Рамблер делай работу хорошо , тогда как mail.ru порезы от плеча .
Чтобы правильно сегментировать или объединить строки, вам необходимо знать, какая фраза наиболее вероятна.
В статистической лингвистике для этой цели используются так называемые языковые модели, которые обычно строятся на основе модели нгграмм (или байесовской сети).
Здесь я не буду подробно объяснять, что это такое.
Читатель может посмотреть мой предыдущий пост , где такая модель создана для простого генератора текста.
Хорошая новость в том, что эту модель можно представить как трансдиссер.
Более того, есть готовые библиотеки, позволяющие рассчитать модель на основе заданного корпуса.
Основная идея состоит в том, чтобы посчитать пары, тройки или n-последовательностей слов, перейти от частот к вероятностям и построить автомат. Эта машина делает простую вещь — оценивает вероятность появления последовательности слов на входе.
Там, где вероятность больше, мы используем эту последовательность.

На рисунке показана языковая модель для нескольких слов.
Картина кажется несколько запутанной, но алгоритм ее построения прост. Однако языковая модель — это тема, требующая отдельной статьи.
Надеюсь написать это в ближайшем будущем.
Веса перехода в языковой модели — это не что иное, как вероятность встретить следующее слово.
Однако для численной стабильности его представляют в виде отрицательного логарифма.
Таким образом, веса превращаются в своего рода штраф, и чем меньше штраф, тем более вероятна данная линия.
Собираем все это вместе
У нас есть все необходимое для создания программы проверки орфографии.Все, что вам нужно сделать, это выполнить композицию из четырех преобразователей: R = S о E о L о M
- S - исходная строка
- E - модель ошибки
- Л - лексикон
- М - языковая модель
Здесь есть пара моментов, которые требуют пояснения.
Во-первых, преобразователь L. Это довольно тривиальный преобразователь, который «склеивает» слово из букв, чтобы передать целое слово на модель.
Таким образом, это помогает перейти от букв и символов в модели ошибок к словам в языковой модели.
Второй момент – это вес преобразователей.
Для составления корректной композиции необходимо, чтобы веса всех преобразователей имели одинаковое значение.
Исходная строка и словарь не имеют весов, языковая модель представляет вероятности, а модель ошибок дает Левенштейна.
Нам нужно перейти от этой оценки к вероятностям.
Этот процесс близок к шаманству, но тем не менее можно подобрать веса, наиболее подходящие для реальных ошибок.
Пожалуй, это все.
Вы можете справедливо спросить, а где код? Но его там нет. Все делается с помощью операций над преобразователями.
И эти операции уже реализованы в библиотеках.
Например, в этом: openfst.org .
Все, что вам нужно сделать, это построить исходные объекты.
Выводы, за и против
Я нахожу этот подход очень интересным.У него есть ряд сильных сторон.
Первая сила в том, что мы не пишем код, а просто оперируем математическими объектами.
Это упрощает разработку инструментов для работы с текстом и экономит массу времени.
Еще одним преимуществом является его универсальность.
Нет необходимости писать разные алгоритмы для операций со строками.
Например, если вам нужно обнаружить некорректные ошибки верстки вида «fkujhbnv» -> «алгоритм», то для этого не нужно писать новую программу.
Достаточно немного модифицировать модель ошибки: добавить переходы, отмеченные буквами двух языков и парой состояний.
Однако есть и отрицательные стороны.
Добиться стабильной и быстрой скорости довольно нетривиально.
Я не мог получить.
Скорость работы сильно зависит от структуры преобразователей, количества переходов и степени недетерминированности.
Кроме того, некоторые операции с преобразователями требуют больших объемов памяти.
Но все эти вопросы так или иначе разрешимы.
Надеюсь, статья была полезной.
Задавайте вопросы, если что-то не понятно.
Я буду рад ответить.
Теги: #Проверка орфографии #Проверка орфографии #алгоритмы #Конечный автомат #Алгоритмы

-
Бедленд
19 Oct, 24 -
12 Книг, Которые Мы Читали
19 Oct, 24 -
Viacom Тайно Загрузила Видео На Youtube
19 Oct, 24 -
Флейта Забытых Снов
19 Oct, 24 -
Понимание C Путем Изучения Ассемблера
19 Oct, 24 -
Где Живут Удаленные Темы?
19 Oct, 24


