Перевод статьи подготовлен специально для студентов курса.

Обучение с подкреплением покорило мир искусственного интеллекта.
Начиная с AlphaGo и АльфаСтар , все большее количество видов деятельности, в которых раньше доминировали люди, теперь контролируются агентами ИИ, работающими на основе обучения с подкреплением.
Короче говоря, эти достижения зависят от оптимизации действий агента в конкретной среде для достижения максимального вознаграждения.
В последних нескольких статьях из ГрадиентПолумесяца мы рассмотрели различные фундаментальные аспекты обучения с подкреплением, от основ систем до бандиты и подходы, основанные на политика , прежде чем оптимизировать поведение на основе вознаграждений в Марковские среды .
Все эти подходы требовали полного знания нашей окружающей среды.
Динамическое программирование , например, требует, чтобы у нас было полное распределение вероятностей всех возможных переходов состояний.
В действительности, однако, мы обнаруживаем, что большинство систем невозможно полностью интерпретировать и что распределения вероятностей не могут быть выведены явно из-за сложности, присущей им неопределенности или вычислительных ограничений.
В качестве аналогии рассмотрим задачу метеоролога — количество факторов, участвующих в прогнозировании погоды, может быть настолько большим, что точно вычислить вероятность невозможно.
В таких случаях решением являются такие методы обучения, как Монте-Карло.
Термин Монте-Карло обычно используется для описания любого подхода к оценке, основанного на случайной выборке.
Другими словами, мы не предсказываем знания о нашем окружении, а учимся на опыте, проходя через примерные последовательности состояний, действий и вознаграждений, получаемых в результате взаимодействия с окружением.
Эти методы работают путем непосредственного наблюдения за вознаграждениями, возвращаемыми моделью во время нормальной работы, чтобы оценить среднее значение ее состояний.
Интересно, что даже без каких-либо знаний о динамике окружающей среды (которую следует рассматривать как распределение вероятностей переходов состояний) мы все равно можем получить оптимальное поведение для максимизации вознаграждения.
В качестве примера рассмотрим результат броска 12 игральных костей.
Рассматривая эти броски как единое состояние, мы можем усреднить эти результаты, чтобы приблизиться к истинному прогнозируемому результату.
Чем больше выборка, тем ближе мы подходим к фактическому ожидаемому результату.
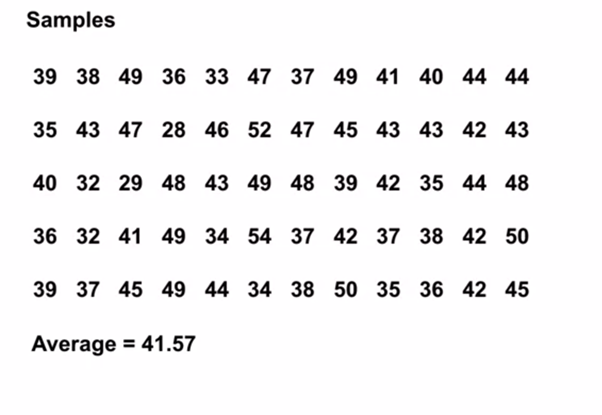
Средняя ожидаемая сумма на 12 кубиках при 60 бросках равна 41,57.
Этот тип оценки на основе выборки может показаться читателю знакомым, поскольку такая выборка выполняется и для k-бандитных систем.
Вместо сравнения разных бандитов методы Монте-Карло используются для сравнения различных политик в марковских средах, определяя ценность государства, поскольку конкретная политика соблюдается до завершения.
Оценка стоимости состояния с использованием методов Монте-Карло
В контексте обучения с подкреплением методы Монте-Карло — это способ оценить значение состояния модели путем усреднения результатов выборки.Из-за необходимости терминального состояния методы Монте-Карло по своей сути применимы к эпизодическим средам.
Из-за этого ограничения методы Монте-Карло обычно считаются «автономными», в которых все обновления выполняются после достижения конечного состояния.
Можно провести простую аналогию с поиском выхода из лабиринта: автономный подход заставит агента дойти до самого конца, прежде чем использовать опыт, полученный между ними, чтобы попытаться сократить время, необходимое для прохождения лабиринта.
С другой стороны, при онлайн-подходе агент будет постоянно менять свое поведение уже во время прохождения лабиринта; возможно, он заметит, что зеленые коридоры ведут в тупики, и решит, например, обходить их стороной.
Мы обсудим онлайн-подходы в следующей статье.
Метод Монте-Карло можно сформулировать следующим образом: 
Чтобы лучше понять, как работает метод Монте-Карло, рассмотрим диаграмму перехода состояний ниже.
Награда за каждый переход состояния отображается черным цветом, и к ней применяется коэффициент дисконтирования 0,5. Давайте пока отложим фактическое значение состояния и сосредоточимся на вычислении результатов одного броска.

Диаграмма перехода состояний.
Номер статуса отображается красным цветом, результат — черным.
Учитывая, что терминальное состояние возвращает результат 0, давайте рассчитаем результат каждого состояния, начиная с терминального состояния (G5).
Обратите внимание, что мы установили коэффициент дисконтирования равным 0,5, что приведет к взвешиванию в сторону более поздних состояний.
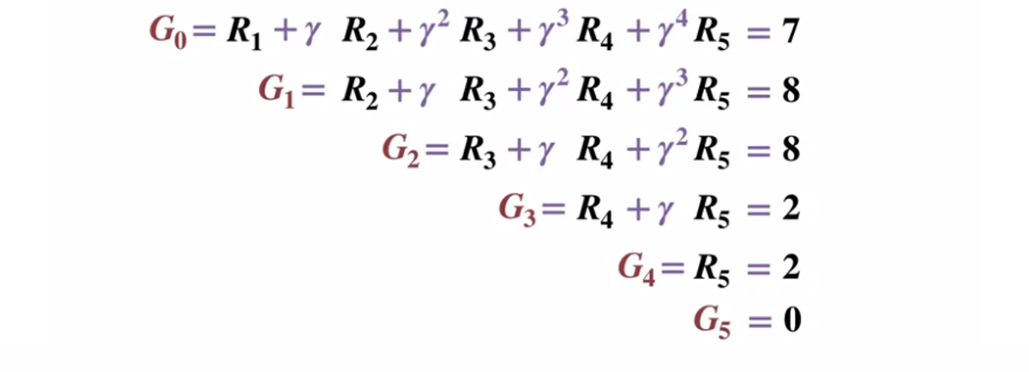
Или в более общем плане: 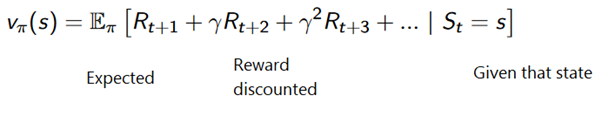
Чтобы избежать хранения всех результатов в списке, мы можем выполнять процедуру обновления значения состояния Монте-Карло постепенно, используя уравнение, которое имеет некоторое сходство с традиционным градиентным спуском: 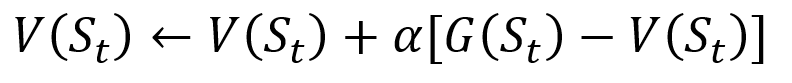
Процедура инкрементного обновления Монте-Карло.
S — это состояние, V — его значение, G — его результат, а A — параметр значения шага.
В рамках обучения с подкреплением методы Монте-Карло можно даже классифицировать как «Первое посещение» или «Каждое посещение».
Короче говоря, разница между ними заключается в том, сколько раз штат можно посетить за один проход до обновления Монте-Карло.
Метод Монте-Карло «Первое посещение» оценивает значение всех состояний как среднее значение результатов после одиночных посещений каждого состояния до завершения задания, а метод Монте-Карло «Каждое посещение» усредняет результаты после n посещений до завершения задания.
заканчивается.
В этой статье мы будем использовать метод «Первое посещение Монте-Карло» из-за его относительной простоты.
Управление политиками с использованием методов Монте-Карло
Если модель не может обеспечить политику, для оценки значений состояния действия можно использовать метод Монте-Карло.Это полезнее, чем просто смысл состояний, потому что представление о смысле каждого действия (к) в этом состоянии позволяет агенту автоматически формировать политику на основе наблюдений в незнакомой среде.
Более формально, мы можем использовать метод Монте-Карло для оценки q(s, а, пи) , ожидаемый результат при старте из состояния s, действия a и последующей политики Пи .
Методы Монте-Карло остаются прежними, за исключением того, что действия, предпринимаемые для конкретного состояния, имеют дополнительное измерение.
Считается, что пара государство-действие (с, а) , посещено за проход, если штат когда-либо посещался с и действие совершается в нем а .
Аналогичным образом, оценка ценностного действия может быть выполнена с использованием подходов «Первое посещение» и «Каждое посещение».
Как и в динамическом программировании, мы можем использовать итерацию обобщенной политики (GPI) для формирования политики на основе наблюдения за значениями состояний действий.
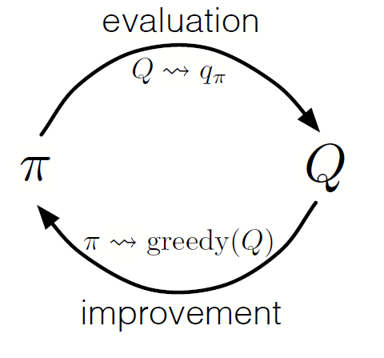
Чередуя этапы оценки политики и ее совершенствования, а также включая исследования, чтобы гарантировать, что все возможные действия пройдены, мы можем достичь оптимальной политики для каждого государства.
Для GPI Монте-Карло это чередование обычно выполняется после окончания каждого прохода.

Монте-Карло GPI
Стратегия блэкджека
Чтобы лучше понять, как метод Монте-Карло работает на практике в задаче оценки различных значений состояний, давайте проведем пошаговую демонстрацию с использованием игры в блэкджек.Для начала определимся с правилами и условиями нашей игры: Мы будем играть только против дилера, других игроков не будет. Это позволит нам рассматривать руки дилера как часть окружающей среды.
Стоимость числовых карт равна их номинальной стоимости.
Стоимость карточек с картинками: Валет, Король и Королева равна 10. Значение Туза может быть 1 или 11 в зависимости от выбора игрока.
Обе стороны получают по две карты.
Две карты игрока лежат лицевой стороной вверх, и одна из карт дилера также лежит лицевой стороной вверх.
Цель игры — собрать общее количество карт на руке.
<=21. A value greater than 21 is a bust; if both sides have a value of 21, then the game is a draw. После того, как игрок увидел свои карты и первую карту дилера, игрок может решить взять ему новую карту («еще») или нет («достаточно») до тех пор, пока он не будет удовлетворен суммой значений карт в своем рука.
Затем дилер показывает свою вторую карту – если полученная сумма меньше 17, он обязан брать карты до тех пор, пока не наберет 17 очков, после чего больше карт не берет. Давайте посмотрим, как с этими правилами работает метод Монте-Карло.
Раунд 1.
Всего у вас получается 19. Но вы пытаетесь поймать удачу за хвост, рискуете, получаете 3 и разоряетесь.
Когда вы разорились, у дилера была только одна открытая карта с общим числом 10. Это можно представить следующим образом: 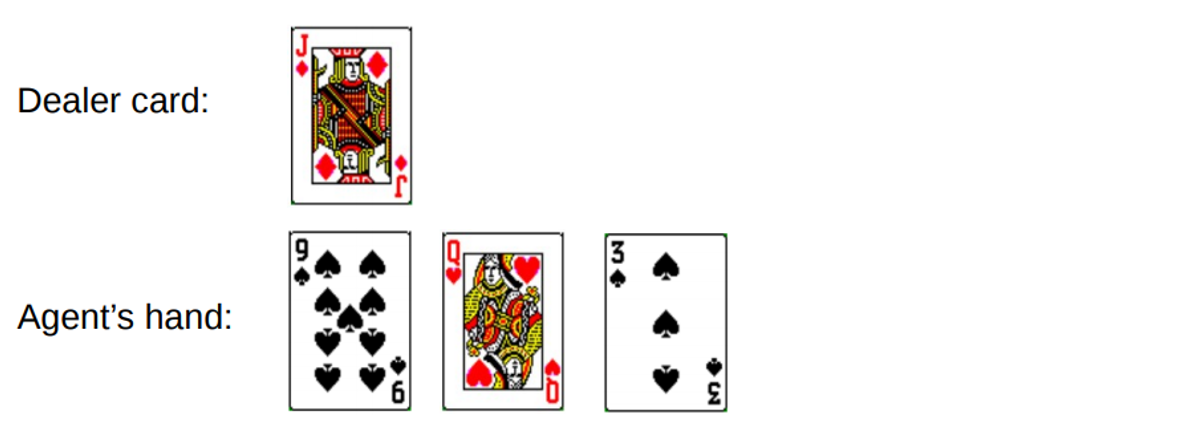
Если мы разоримся, наша награда за раунд будет -1. Давайте назначим это значение как возвращаемый результат предпоследнего состояния, используя следующий формат [Сумма агента, Сумма дилера, Туз?]: 
Ну, нам сейчас не повезло.
Перейдем к другому раунду.
Раунд 2.
Всего вы достигаете 19. На этот раз вы решаете остановиться.Дилер набирает 13, забирает карту и разоряется.
Предпоследнее состояние можно описать следующим образом.

Опишем состояния и награды, которые мы получили в этом раунде: 
По окончании прохода мы теперь можем обновить значения всех наших состояний в этом раунде, используя вычисленные результаты.
Установив коэффициент дисконтирования равным 1, мы просто распределяем наше новое вознаграждение между руками, как мы это делали ранее с переходами состояний.
Поскольку государство В(19, 10, нет) ранее возвращенное -1, мы вычисляем ожидаемое возвращаемое значение и присваиваем его нашему состоянию: 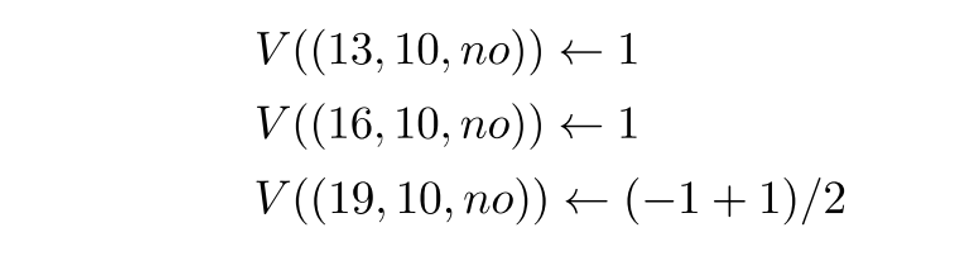
Итоговые значения состояния для демонстрации на примере блэкджека .
Выполнение
Давайте напишем игру в блэкджек, используя метод Монте-Карло первого посещения, чтобы узнать все возможные значения состояния (или различные комбинации рук) в игре с использованием Python. Наш подход будет основан на подход Судхарсана и др.ал.
.
Как обычно, весь код из статьи вы можете найти по адресу наш GitHub .
Для упрощения реализации мы будем использовать тренажер от OpenAI. Рассматривайте среду как интерфейс для запуска игры в блэкджек с минимальным количеством кода.
Это позволит нам сосредоточиться на реализации обучения с подкреплением.
Удобно, что вся собранная информация о состояниях, действиях и наградах хранится в переменных.
"наблюдение" , которые накапливаются в ходе текущих игровых сессий.
Давайте начнем с импорта всех библиотек, которые нам понадобятся, чтобы получить и собрать наши результаты.
Далее давайте инициализируем нашу среду спортзал и определить политику, которая будет координировать действия нашего агента.import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use(‘ggplot’)
По сути, мы будем продолжать брать карту до тех пор, пока сумма на нашей руке не достигнет 19 или более, после чего мы остановимся.
#Observation here encompassess all data about state that we need, as well as reactions to it
env = gym.make(‘Blackjack-v0’)
#Define a policy where we hit until we reach 19.
# actions here are 0-stand, 1-hit
def sample_policy(observation):
score, dealer_score, usable_ace = observation
return 0 if score >= 19 else 1
Давайте определим метод для генерации проходных данных с помощью нашей политики.
Мы будем хранить информацию о статусе, предпринятых действиях и вознаграждениях за действия.
def generate_episode(policy, env):
# we initialize the list for storing states, actions, and rewards
states, actions, rewards = [], [], []
# Initialize the gym environment
observation = env.reset()
while True:
# append the states to the states list
states.append(observation)
# now, we select an action using our sample_policy function and append the action to actions list
action = sample_policy(observation)
actions.append(action)
# We perform the action in the environment according to our sample_policy, move to the next state
observation, reward, done, info = env.step(action)
rewards.append(reward)
# Break if the state is a terminal state (i.e. done)
if done:
break
return states, actions, rewards
Наконец, давайте определим функцию прогнозирования первого посещения Монте-Карло.
Сначала мы инициализируем пустой словарь для хранения текущих значений состояния и словарь для хранения количества записей для каждого состояния в разных проходах.
def first_visit_mc_prediction(policy, env, n_episodes):
# First, we initialize the empty value table as a dictionary for storing the values of each state
value_table = defaultdict(float)
N = defaultdict(int)
Для каждого прохода мы вызываем наш метод генерировать_эпизод получать информацию о государственных ценностях и вознаграждениях, полученных после наступления состояния.
Мы также инициализируем переменную для хранения дополнительных результатов.
Затем мы получаем вознаграждение и значение текущего состояния для каждого состояния, посещенного во время обхода, и увеличиваем нашу возвращаемую переменную на значение вознаграждения за шаг.
for _ in range(n_episodes):
# Next, we generate the epsiode and store the states and rewards
states, _, rewards = generate_episode(policy, env)
returns = 0
# Then for each step, we store the rewards to a variable R and states to S, and we calculate
for t in range(len(states) — 1, -1, -1):
R = rewards[t]
S = states[t]
returns += R
# Now to perform first visit MC, we check if the episode is visited for the first time, if yes,
#This is the standard Monte Carlo Incremental equation.
# NewEstimate = OldEstimate+StepSize(Target-OldEstimate)
if S not in states[:t]:
N[S] += 1
value_table[S] += (returns — value_table[S]) / N[S]
return value_table
Напомню, поскольку мы реализуем first-visit Monte Carlo, то посещаем одно государство за один проход. Поэтому мы выполняем условную проверку словаря состояний, чтобы узнать, было ли посещено состояние.
Если это условие выполняется, мы можем вычислить новое значение, используя процедуру обновления состояния Монте-Карло, определенную ранее, и увеличить количество наблюдений для этого состояния на 1. Затем мы повторяем процесс для следующего прохода, чтобы в конечном итоге получить среднее значение.
результата.
Давайте запустим то, что у нас есть, и посмотрим на результаты! value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000)
for i in range(10):
print(value.popitem())
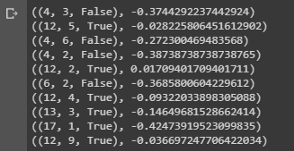
Вывод образца, показывающий значения состояний различных комбинаций на руках в блэкджеке.
Мы можем продолжать проводить наблюдения методом Монте-Карло для 5000 запусков и построить распределение значений состояния, которое описывает значения любой комбинации, имеющейся у игрока и дилера.
def plot_blackjack(V, ax1, ax2):
player_sum = np.arange(12, 21 + 1)
dealer_show = np.arange(1, 10 + 1)
usable_ace = np.array([False, True])
state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace)))
for i, player in enumerate(player_sum):
for j, dealer in enumerate(dealer_show):
for k, ace in enumerate(usable_ace):
state_values[i, j, k] = V[player, dealer, ace]
X, Y = np.meshgrid(player_sum, dealer_show)
ax1.plot_wireframe(X, Y, state_values[:, :, 0])
ax2.plot_wireframe(X, Y, state_values[:, :, 1])
for ax in ax1, ax2: ax.set_zlim(-1, 1)
ax.set_ylabel(‘player sum’)
ax.set_xlabel(‘dealer sum’)
ax.set_zlabel(‘state-value’)
fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'})
axes[0].
set_title('state-value distribution w/o usable ace') axes[1].
set_title('state-value distribution w/ usable ace')
plot_blackjack(value, axes[0], axes[1])
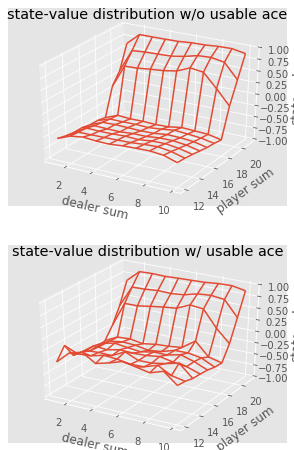
Визуализация значений состояний различных комбинаций в блэкджеке.
Итак, давайте подведем итог тому, что мы узнали.
Методы обучения на основе выборки позволяют нам оценивать значения состояния и состояния-действия без какой-либо динамики перехода, просто путем выборки.
Подходы Монте-Карло основаны на случайной выборке модели, наблюдении за вознаграждениями, возвращаемыми моделью, и сборе информации во время нормальной работы для определения среднего значения ее состояний.
Используя методы Монте-Карло, возможна обобщенная итерационная политика.
Ценность всех возможных комбинаций в руках игрока и дилера в блэкджеке можно оценить посредством многократного моделирования Монте-Карло, что открывает путь для оптимизации стратегий.
На этом завершается введение в метод Монте-Карло.
В нашей следующей статье мы перейдем к методам обучения типа «Временная разница».
Источники:
Саттон и др.др.
, Обучение с подкреплением Уайт и др.
al, Основы обучения с подкреплением, Университет Альберты Сильва и др.
al, Обучение с подкреплением, UCL Платт и др.
Эл, Северо-Восточный университет Вот и все.
Увидимся в курс ! Теги: #Машинное обучение #искусственный интеллект #ИИ #машинное обучение #обучение с подкреплением #Блэкджек #Монте-Карло

-
Linux Для Домашних Пользователей
19 Oct, 24 -
Сравнение Планов Базы Данных Списков Ячеек
19 Oct, 24 -
Обогащение Руды
19 Oct, 24 -
Рейтинг Комментариев
19 Oct, 24 -
Факторы Социальной Реализации Пользователей
19 Oct, 24


