Я долго готовился и собирал материал, надеюсь, в этот раз получилось лучше.
Эту статью я посвящаю основным методам решения задач математической оптимизации с ограничениями, поэтому, если вы слышали, что симплексный метод – это своего рода очень важно метод, но до сих пор не знаете, что он делает, то, возможно, эта статья вам поможет. 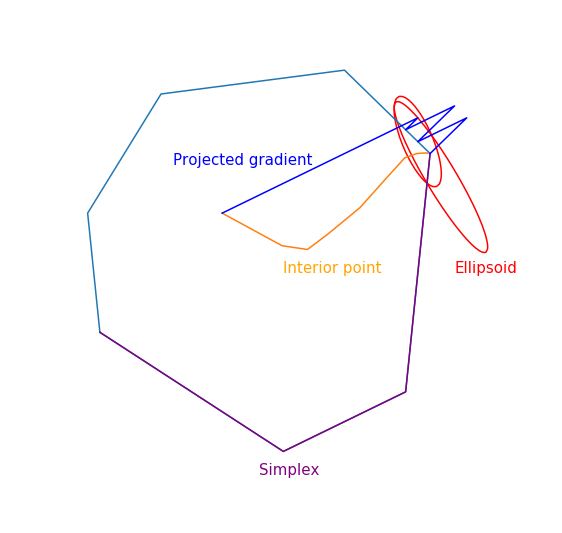
P. S. В статье приведены математические формулы, добавленные макросами хабраредора.
Говорят, иногда не появляются.
Также имеется множество анимаций в формате gif.
Преамбула
Задача математической оптимизации представляет собой задачу вида «Найти в множествеэлемент
такой, что для каждого
от
выполненный
", что в научной литературе, скорее всего, было бы написано примерно так
Исторически сложилось так, что популярные методы, такие как градиентный спуск или метод Ньютона, работают только в линейных пространствах (и желательно простых, например
).
На практике часто возникают задачи, когда нужно найти минимум в нелинейном пространстве.
Например, вам нужно найти минимум какой-либо функции на таких векторах.
, для которого
, это может быть связано с тем, что
указать длины некоторых предметов.
Или, например, если
представляют собой координаты точки, которая должна быть не более
от
, т.е.
.
Для таких задач нельзя напрямую применить градиентный спуск или метод Ньютона.
Оказалось, что очень большой класс задач оптимизации удобно охватить «ограничениями», подобными тем, которые я описал выше.
Другими словами, удобно представить множество
в виде системы равенств и неравенств
Проблемы минимизации пространства обзора
Таким образом, их стали условно называть «неограниченными задачами», а задачи над множествами, определяемыми множествами равенств и неравенств, – «ограниченными задачами».
Технически абсолютно любой набор
можно представить в виде одного равенства или неравенства, используя индикатор -функция, которая определяется как
однако такая функция не обладает различными полезными свойствами (выпуклостью, дифференцируемостью и т. д.).
Однако часто можно представить
в виде нескольких равенств и неравенств, каждое из которых обладает такими свойствами.
Основную теорию резюмирует случай
Где
— выпуклые (но не обязательно дифференцируемые) функции,
- матрица.
Чтобы продемонстрировать, как работают методы, я буду использовать два примера:
- Задача линейного программирования
По сути, эта задача состоит в том, чтобы найти самую дальнюю точку многоугольника в направлении (2, 1), решением задачи является точка (4.7, 3.5) — «самая правая» в многоугольнике).А вот и сам полигон

- Минимизация квадратичной функции с одним квадратичным ограничением
Симплексный метод
Из всех методов, о которых я рассказываю в этом обзоре, симплексный метод, пожалуй, самый известный.Метод был разработан специально для линейного программирования и является единственным из представленных, позволяющим добиться точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика; на практике это обычно не так, но в теории это возможно).
).
Идея симплекс-метода состоит из двух частей:
- Системы линейных неравенств и равенств определяют многомерные выпуклые многогранники (многогранники).
В одномерном случае это точка, луч или отрезок, в двумерном – выпуклый многоугольник, в трехмерном – выпуклый многогранник.
Минимизация линейной функции — это, по сути, поиск «самой дальней» точки в определенном направлении.
Я думаю, интуиция должна подсказать, что эта самая дальняя точка должна быть какой-то вершиной, и это действительно так.
В целом для системы
неравенство в
В -мерном пространстве вершина — это точка, удовлетворяющая системе, для которой ровно
этих неравенств превращаются в равенства (при условии, что среди неравенств нет эквивалентных).Таких точек всегда конечное число, хотя их может быть много.
- Теперь у нас есть конечное множество точек; вообще говоря, мы можем просто взять их и пройтись по ним, то есть сделать что-то вроде этого: для каждого подмножества
неравенства, решить систему линейных уравнений на основе выбранных неравенств, проверить соответствие решения исходной системе неравенств и сравнить с другими такими же точками.Это достаточно простой, малоэффективный, но рабочий метод. Симплексный метод вместо перебора перемещается от вершины к вершине по ребрам таким образом, что значения целевой функции улучшаются.
Получается, что если у вершины нет «соседей», у которых значения функции лучше, то она оптимальна.
Для таких методов нужно с чего-то начинать, обычно это делается путем решения вспомогательной задачи
Если решить эту проблему
такой, что
, то оно выполняется
, в противном случае исходная задача обычно задается на пустом множестве.
Для решения вспомогательной задачи можно воспользоваться и симплексным методом, но за отправную точку можно взять
с произвольным
.
Поиск исходной точки можно условно назвать первым этапом метода, поиск решения исходной задачи можно условно назвать вторым этапом метода.
Траектория двухфазного симплекс-метода Траектория была создана с помощью scipy.optimize.linprog. 
Проективный градиентный спуск
Недавно я написал отдельную статью о градиентном спуске.статья , в которой он кратко описал этот метод. Сейчас этот метод вполне жив, но изучается как часть более общего.
проксимальный градиентный спуск .
Сама идея метода совершенно банальна: если применить градиентный спуск к выпуклой функции
, то при правильном выборе параметров получим глобальный минимум
.
Если после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее ее проекцию на замкнутое выпуклое множество
, то в результате получим минимум функции
на
.
Ну, или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет
Где
Последнее равенство определяет стандартный оператор проецирования на множество; по сути, это функция, которая в какой-то момент
вычисляет ближайшую к нему точку множества
.
Расстояние здесь играет роль
, стоит отметить, что здесь можно использовать любые норма , однако прогнозы по разным стандартам могут отличаться!
На практике проективный градиентный спуск используется только в особых случаях.
Основная его проблема в том, что расчет проекции может быть даже сложнее исходной, и ее нужно рассчитывать много раз.
Самый распространенный случай, для которого удобно использовать проективный градиентный спуск, — это «коробочные ограничения», которые имеют вид
В этом случае проекция рассчитывается очень просто, для каждой координаты получаем
Использовать проективный градиентный спуск для задач линейного программирования совершенно бессмысленно, однако, если вы это сделаете, то это будет выглядеть примерно так Проективная траектория градиентного спуска для задачи линейного программирования 
А вот как выглядит траектория проективного градиентного спуска для второй задачи, если выберите большой размер шага 
и если выберите маленький размер шага 
Эллипсоидный метод
Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования; это можно считать многомерным обобщением метод деления пополам .Я начну с чего-то более общего метод разделяющей гиперплоскости :
- На каждом шаге метода существует определенное множество, содержащее решение задачи.
- На каждом шаге строится гиперплоскость, после чего из множества удаляются все точки, лежащие по одну сторону от выбранной гиперплоскости, и, возможно, к этому множеству добавляются какие-то новые точки.
Если вы исправите
, то для выпуклой функции
полупространство
содержит только точки со значением не меньше точки
, а значит, их можно отрезать, так как эти точки ничем не лучше той, которую мы уже нашли.
В случае проблем с ограничениями вы можете аналогичным образом избавиться от точек, которые гарантированно нарушают некоторые ограничения.
Самый простой вариант метода разделяющей гиперплоскости — просто отрезать полупространства без добавления точек.
В результате на каждом шаге у нас будет определенный многогранник.
Проблема этого метода в том, что количество граней многогранника, скорее всего, будет увеличиваться от шага к шагу.
Более того, он может расти в геометрической прогрессии.
Метод эллипсоида фактически сохраняет эллипсоид на каждом шаге.
Точнее, после рисования гиперплоскости строится эллипсоид минимального объема, содержащий одну из частей исходного.
Этого можно добиться добавлением новых точек.
?Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом:
Построение эллипсоида минимального объема, содержащего пересечение полупространства и другого эллипсоида, можно выполнить с помощью умеренно громоздкие формулы .
К сожалению, на практике этот метод оказался все же не так хорош, как симплекс-метод или метод внутренней точки.
Но на самом деле, как это работает для линейное программирование 
и для квадратичное программирование 
Метод внутренней точки
Этот метод имеет долгую историю развития; некоторые из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод. Но на тот момент оно еще не было достаточно эффективным, чтобы его можно было использовать на практике.Позже в 1984 году был разработан вариант метод, специально предназначенный для линейного программирования, который был хорош как в теории, так и на практике.
Более того, метод внутренней точки не ограничивается линейным программированием, как симплексный метод, и в настоящее время является основным алгоритмом для задач выпуклой оптимизации с ограничениями.
Основная идея метода заключается в замене ограничений штрафом в виде так называемой барьерная функция .
Функция
называется барьерная функция для набора
, Если
Здесь
- внутри
,
- граница
.
Вместо исходной задачи предлагается решить задачу
И
устанавливал только на внутренности
(по сути, отсюда и название), свойство барьера гарантирует, что
минимум
существует. Более того, чем больше
, тем больше влияние
.
При достаточно разумных условиях этого можно добиться, если стремиться
до бесконечности, то минимум
будет сходиться к решению исходной задачи.
Если набор
задано в виде набора неравенств
, то стандартный выбор барьерной функции будет логарифмический барьер
Минимум баллов
функции
для разных
образует кривую, которую обычно называют центральный путь , метод внутренней точки пытается следовать по этому пути.
Вот как это выглядит Пример с линейным программированием 
Аналитический центр - это просто
Наконец, сам метод внутренней точки выглядит так:
- Выберите начальное приближение
, - Выберите новое приближение, используя метод Ньютона.
- Увеличивать
И, наконец, вот как выглядит траектория метода внутренней точки Задача линейного программирования 
Прыгающая черная точка – это
, т.е.
точка, к которой мы пытаемся приблизиться методом Ньютона на текущем шаге.
Задача квадратичного программирования 
Теги: #математика #Алгоритмы #линейные системы и оптимизация

-
Кредитные Калькуляторы
19 Oct, 24 -
Беспроводные Сети Hp
19 Oct, 24


