«Крестики-нолики» — игра, изученная вдоль и поперек, и разработка ИИ для нее может сводиться к организации дерева решений, описанного в Википедия .
В этой статье будет рассмотрено решение игры с использованием обучения с подкреплением и аппроксимации функций ценности.
Подготовка
Примем следующие правила:- Агент ходит первым и играет крестиками.
- Агент будет принимать только те решения, которые имеют максимальную ценность.
- Существует 5%-ная вероятность того, что агент примет зондирующие решения.
- Только в случае победы агент получает вознаграждение.
В нашем случае функцией значения будет таблица состояний игры, в которой значение от 0 до 1 будет указывать на то, что то или иное состояние «лучше» другого.
Изначально мы установили в нашей таблице, что все выигрышные комбинации (три крестика в ряду, столбце или по диагонали) дают вероятность, равную 1. Аналогично все состояния с тремя нулями – 0. Для всех остальных состояний вероятность равна 0,5. 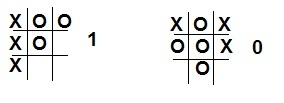
Для упрощения составления таблицы вероятностей будем считать, что всего
состояния.
Конечно, половина этих комбинаций невозможны, но и оптимизировать код смысла не было.
Код инициализации таблицы вероятностей
float V[19683]; //------- void setV(int a1,int a2,int a3,int b1,int b2,int b3,int c1,int c2,int c3,float v) { int num; num = ((((((((a1*3)+a2)*3+a3)*3+b1)*3+b2)*3+b3)*3+c1)*3+c2)*3+c3; V[num] = v; } //------- for (int i1=0;i1<3;i1++) for (int i2=0;i2<3;i2++) for (int i3=0;i3<3;i3++) for (int i4=0;i4<3;i4++) for (int i5=0;i5<3;i5++) for (int i6=0;i6<3;i6++) for (int i7=0;i7<3;i7++) for (int i8=0;i8<3;i8++) for (int i9=0;i9<3;i9++) { setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0.5); if (i1==i2 && i2==i3 && i3==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i4==i5 && i5==i6 && i6==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i7==i8 && i8==i9 && i9==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i1==i5 && i5==i9 && i9==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i7==i5 && i5==i3 && i3==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i1==i4 && i4==i7 && i7==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i2==i5 && i5==i8 && i8==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i3==i6 && i6==i9 && i9==1) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,1); if (i1==i2 && i2==i3 && i3==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i4==i5 && i5==i6 && i6==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i7==i8 && i8==i9 && i9==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i1==i5 && i5==i9 && i9==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i7==i5 && i5==i3 && i3==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i1==i4 && i4==i7 && i7==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i2==i5 && i5==i8 && i8==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); if (i3==i6 && i6==i9 && i9==2) setV(i1,i2,i3,i4,i5,i6,i7,i8,i9,0); }
Ход игры
Противником будет человек, который соответственно будет играть на нули и периодически сдаваться.В ходе игры значение его состояний будет меняться.
Чтобы правильно оценить действия агента, необходимо записать последовательность состояний, которые он выбрал, и пересчитать их в конце игры.
Формула расчета значения V(s) будет следующей:
,
где A — размер шага, влияющий на скорость обучения.
V(s') — ценность действия в конце игры (1 — в случае победы, 0 — в противном случае).
Размер шага влияет на то, изменится стратегия противника или нет. Если необходимо учитывать вариативность стратегии, то размер шага необходимо оставить постоянным.
В противном случае, когда шаг уменьшится до нуля, агент прекратит обучение.
Использование пробных ходов (не имеющих высокого значения) позволяет проверять условия, которые из-за высокого значения других ходов никогда не будут выполнены, что дает небольшой шанс на изменение стратегии в выигрышную сторону.
Код выбора перемещения агента void stepAI(void)
{
int flag;
c_var=0;
for (int i=0;i<19683;i++)
{
flag=0;
readMap(i);
for (int j=1; j<10;j++)
if (rm[j]!=m[j])
if ((m[j]==0) && (rm[j]==1)) flag++;
else flag+=2;
if (flag==1) {
var[c_var]=i;
c_var++;
}
}
float v_max;
int v_num_max;
if (random(100)<5) v_num_max=random(c_var);
else {
v_max = V[var[0]];
v_num_max = 0;
if (c_var>1)
for (int i=1;i<c_var;i++)
if (V[var[i]]>v_max)
v_num_max = i;
}
steps++;
steps_m[steps]=var[v_num_max];
readMap(var[v_num_max]);
for (int i=1;i<10;i++)
m[i]=rm[i];
paintMap();
}
В приведенном выше коде выбираются возможные ходы (состояния, в которых элементы идентичны текущему состоянию поля, а также имеется еще один крестик).
Затем из полученных состояний выбирается либо случайный ход (с вероятностью 5%), либо «жадный» ход (с максимальным значением).
По завершении выбора этот ход записывается в отдельный массив сделанных ходов.
В конце игры, как уже говорилось, ценность сделанных ходов пересчитывается.
Пересчет стоимости void learnAI(int res)
{
for (int i=0;i<steps;i++)
V[steps_m[i]] += A * (res - V[steps_m[i]]);
A -= 0.01;
}
Нижняя граница
→ Программа и проект в C++ Builder 6 В этом примере кратко рассмотрен один аспект обучения с подкреплением.Если агент обычно контактирует с окружением, то в данном примере обучение проводилось на вражеском игроке.
Хотя этот пример достаточно прост, может показаться, что этот метод в других примерах будет весьма ограничен, чем есть на самом деле.
Подержанные книги
Обучение с подкреплением / Р.С.
Саттон, Л.
Г.
Барто - Москва: БИНОМ.
Лаборатория знаний, 2014 г.
Теги: #q-learning #Машинное обучение
-
Встраивание Кода И Опасность Пиратского По
19 Oct, 24 -
Юбка Хикару Своими Руками
19 Oct, 24 -
Репозиторий С Задачами Ruby
19 Oct, 24 -
Авторские Права При Ретрансляции В Блоги
19 Oct, 24


