Привет, хабр!
В этом посте пойдет речь о моем участии в конкурсе Ludum Dare 34, который прошел около трех недель назад.
В результате получилась головоломка под названием Growing Sakura, геймплей которой можно увидеть в гифке (не пугайтесь, она весит всего 300Кб): 
Коротко о правилах игры: изначально у нас есть шестиугольное поле и несколько корневых почек (или одна, как на гифке выше).
Из него можно запустить 3 ветки (двумя способами - по клику левой или правой кнопкой мыши).
Из каждой почки на ветке можно левой кнопкой мыши сделать Y-ветвь, а правой кнопкой мыши просто продолжить ветку дальше (I-ветвь).
Если ветка не может расти ни в каком направлении (соответствующая ячейка занята или в нужном направлении нет ячейки), то ветка не растет. В соответствии с последним условием необходимо правильно выбрать порядок «разворачивания» ветвей.
В результате получится дерево (или несколько деревьев) такое, что между двумя соседними ветвями нет острых углов.
Цель игры – охватить все клетки игрового поля.
Не заглядывая под кат, попробуйте на 10 секунд подумать и оценить, насколько сложной может быть эта игра.
Что за Людум Дэйр? Этот конкурс проводится раз в 4 месяца и на этот раз это уже 34-е мероприятие.
Суть конкурса (в номинации «Компо»): вам необходимо в течение 48 часов создать компьютерную игру на заданную тему.
Тема становится известна в первые минуты соревнований.
Игра должна быть создана самостоятельно и с нуля (все с нуля: код, графика, звуки и т.д.), однако допускается использование сторонних программ и кодовых разработок, но они должны быть анонсированы заранее (например, напишите в своем блоге на сайте Ludum Dare: «Я буду использовать Paint, Unity, C++ и Delphi, вот ссылка на шаблон стартового проекта»).
Существует также упрощенная, расслабляющая категория Jam, где вы можете сделать игру с помощью командой до 72 часов, используйте старые разработки и даже (о ужас!) даже не нужно публиковать исходники в конце вместе с игрой.
Однако номинация на Джем меня лично не интересует; иногда переключаюсь на него, только если не успею выполнить его в течение 48 часов.
Тема конкурса определяется голосованием, и на этот раз наибольшее количество голосов получили две темы: «Растущая» и «Управление двумя кнопками».
Вы можете использовать одну из этих тем или обе.
Интерпретация темы оставлена на усмотрение участника: например, первую тему можно трактовать как «Рост», «Взросление» или «Взросление», а вторую — «Управление двумя кнопками» или «Взросление».
«Сила двух кнопок».
Как вы можете видеть из описания игры выше, я в каком-то смысле объединил обе темы вместе.
Первый день Когда я проснулся, соревнование продолжалось уже пару часов.
Никаких очевидных решений тема не предлагала.
Медленно завтракая и наливая кофе, я думал о чем-нибудь интересном, чтобы вписаться в эту тему.
Конечно, мне хотелось объединить обе темы вместе.
Появилось несколько концепций:
- Головоломка, эмулирующая оконный менеджер: на экране много окон (по две кнопки!), нужно их все закрыть, но все усложняется тем, что обе доступные кнопки иногда выполняют весьма хитрые действия (для например, закройте окно справа от этого).
В шутку была идея сделать окна с заголовком «Согласен», заполненные текстом типа «Бла-бла-бла-бла» с двумя кнопками «Согласен» и «Не согласен», которые просто закрывают это окно.
- Стратегия-рогалик: развитие подземной базы.
База состоит из квадратных плиток, с каждой из которых можно совершить одно из двух действий, расширяя таким образом (растя!) базу.
- Какой-то странный механизм, состоящий из кучи блоков, у каждого блока по две кнопки «Включить» и «Выключить».
- Опять стратегия, на этот раз минималистский клон Settlers II. Плитки шестиугольные, и вы снова можете сделать с ними одно из двух (больше дорог или построить дом).
Идея заключалась в том, чтобы строить более крутые здания, нужно было соединить с плиткой несколько дорог.
Но эксперименты на бумаге показали, что дороги почему-то быстро закончились, что остановило рост поселения.
Еще была идея сделать клон Super Hexagon (там управление двумя кнопками!), но я отказался от этой идеи, так как там не было "Растущего".
К середине дня возникла следующая концепция, которая была достигнута за счет упрощения представления о поселенцах:
- Имеется шестиугольное поле, в некоторых ячейках лежат камни, в некоторых — бобы.
А еще нам предстоит вырастить из фасоли корни некоторых растений.
Корни выращивают по правилам, которые были описаны в самом начале этого поста.
Для каждого боба мы знаем, сколько клеток должна покрыть корневая система, чтобы бобовое дерево выросло большим и здоровым.
Ну а задача игрока — вырастить корни, чтобы выросли все бобы.
Назовем точки пересечения вершин треугольников узлами; Из каждого узла исходят 6 ребер.
Некоторые ребра окрашены в красный цвет, а между любыми двумя соседними сверху красными ребрами имеется либо 120 градусов, либо 180 (острых углов нет).
Докажите, что существуют два узла, из одного из которых невозможно попасть в другой, двигаясь по красным ребрам.
Поэтому я просто предположил, что, следуя этим правилам, можно составить довольно сложную головоломку.
Я быстро набросал прототип игровой механики: 
И я увидел, что это хорошо!
В конце первого дня идея выращивания корней трансформировалась в идею выращивания веток вишни (но в коде игры все объекты по-прежнему названы по корням!).
Для упрощения игры все цифры были выброшены и цель свелась к простейшей формулировке: просто охватить все игровое поле.
Прототип игры вырос до следующего: 
Идея заключалась в том, чтобы сделать ветки дерева толще в соответствии с расстоянием до самого дальнего листа (и это видно на гифке).
Однако для длинных ветвей растяжение становилось настолько большим, что портился их внешний вид. Я потратил довольно много времени на то, чтобы все получилось красиво.
В конце концов я забил – предстояло еще много дел.
Отныне все ветки оставались одинаковой толщины.
На этом я решил закончить первый день и лег спать.
Второй день Как обычно, я решил не экономить на сне после первого дня, а не спал на вторую ночь.
Утром я сел и придумал уровни.
Я даже нарисовал шестиугольную сетку в Word и распечатал ее, используя карандаш и ластик.
Стало понятно, что без автоматического решателя дальше будет сложно.
Сказано - сделано.
Я набросал простую программу для решения головоломок на C++.
Он рекурсивно перебирает все возможные действия игрока и смотрит, решена головоломка или нет. На каждой итерации поиска текущее состояние игры сохраняется в std::set. Если позже будет найдено такое же состояние игры, то поиск откатывается.
Таким образом, решатель не рассматривает сто раз одни и те же варианты развития событий.
Оказалось, что упомянутая выше головоломка в двух гифках (назовем ее головоломкой А) имеет целых 47 различных решений.
Полный поиск занял 93 секунды, было рассмотрено 10 810 046 игровых состояний.
Этот решатель очень помог в будущем.
Пример решателя, работающего для другого уровня: 
Этот уровень был решен за 7 секунд, в std::set было сохранено 711211 состояний и было найдено ровно одно решение.
Странная строка в самом низу - это описание уровня, которое вставлено в саму игру.
Чуть позже решатель был оптимизирован с использованием эвристики «одинокой ячейки».
А именно: если на каком-то шаге одна из свободных ячеек была окружена занятыми клетками («стенками» или ячейками, в которые уже проросли ветки сакуры), и нельзя было отправить ветку в эту ячейку из соседних - тогда становилось понятно что здесь решений нет и поиск откатился.
После добавления этой эвристики головоломка А была обработана за 5 секунд, при этом было учтено всего 723 225 состояний.
До конца второго дня я рисовал руками интересные игровые сетки и решал их с помощью своей программы.
А пока я добавил в игру меню (ну а что еще можно сделать, когда решатель пробует решения?), перерисовал иконки.
Игра стала выглядеть так: 
Как видно из гифки, я поставил перед собой довольно амбициозную цель: разработать целых 40 головоломок.
К моменту создания гифки было готово только 17 уровней из 40. До окончания соревнований оставалась еще одна ночь, а именно около 10 часов.
Некоторые уровни генерировались следующим образом: рисовалась какая-то симметричная фигура, в случайную ячейку которой тыкалась корневая почка.
После этого был запущен решатель.
Если полученных решений было слишком много или вообще не было, уровень немного модифицировали (немного меняли форму или пересаживали корневой росток куда-то еще) и запускали решатель заново, и так до тех пор, пока не был построен подходящий уровень.
На других уровнях фигура была намеренно асимметричной; обычно несколько ветвей сакуры сходились в общий «комок», после чего их приходилось аккуратно переплетать друг с другом.
Эти уровни также были созданы с помощью решателя.
Затем я начал добавлять слои с несколькими корневыми почками.
Игра сразу стала намного разнообразнее! Пример уровня с несколькими бутонами: 
Да, иногда не получится закрыть всего одну ячейку, чтобы пройти уровень.
Ночью я добавил в игру экран с правилами игры, создал несколько звуков с помощью замечательной программы Bosca Ceoil и, наконец, прошел все 40 уровней (сорок, Карл!), как и планировалось.
Последние уровни настолько сложны, что мой решатель не отвечает полностью: он находит несколько решений перед собой, затем ему не хватает памяти и он вылетает. Поэтому я не знаю точно, сколько существует решений, хотя можно с уверенностью сказать, что все головоломки в игре имеют решение.
Игра была закончена в последний час и с ослабевшими руками была размещена на сайте соревнований.

После завершения конкурса организаторы отводят на голосование 3 недели.
Участники Ludum Dare скачивают игры других участников и оценивают их.
Я тоже занимался этим около недели и при этом продолжал думать о том, насколько сложной может быть игра «Растущая Сакура».
В итоге всё вылилось в следующее: Выращивание Сакуры НП-сложно Здесь я попытаюсь представить свое доказательство (надеюсь, я нигде его не напортачил!).
В Эта статья можно найти доказательство того, что задача проверки существования гамильтонова цикла в плоском кубическом 3-связном графе является NP-полной (для краткости назовем ее задачей X).
Сразу расшифрую все непонятные слова: График - это несколько точек (они называются вершинами), некоторые пары из которых соединены линиями (они называются ребрами).
График называется плоский можно ли его разместить на плоскости так, чтобы края не пересекались.
График называется кубический , если из каждой его вершины выходят ровно 3 ребра.
График называется 3-связный , если для того, чтобы разорвать его хотя бы на 2 части, нужно удалить минимум 3 ребра.
Цикл Гамильтона в графе – это последовательность попарно различных вершин v 1 ,в 2 ,…, в н такой, что v я и в я +1 соединены ребром для любой 1<=i н и в 1 , где n — количество вершин в графе.
Например, на следующем рисунке показан гамильтонов цикл в плоском кубическом 3-связном графе: 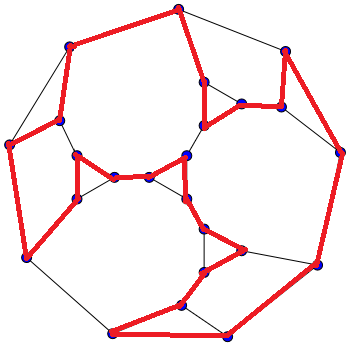
Определение NP-трудности и NP-полноты не так просто.
Но я постараюсь кратко изложить суть дела под спойлером.
Скучно про всякие НП Проблема разрешимости ( проблема решения ) – вопрос, сформулированный в рамках некоторой формальной системы, на который можно ответить «да» или «нет».
Например, вопрос «Дано x и y, верно ли, что x делится на yЭ» является проблемой разрешимости.
Но вопрос «Сколько будет стоить А+ВЭ» не является разрешимой задачей.
Она: ответь мне, только честно, да или нет, ладно? Он: спроси Она: почему мужчины смеются над блондинками? Он: да ( болтать о проблеме решения )Класс НП — множество задач о разрешимости, для которых ответ «да» можно проверить за полиномиальное время при наличии некоторой дополнительной информации (так называемая сертификат ).
При этом для любых входных параметров, если ответ «да», сертификат должен существовать (а не так, что для каких-то входных данных при ответе «да» он существует, а для каких-то нет).
Например, для задачи разрешимости «Вот граф G с n вершинами, верно ли, что он имеет гамильтонов циклЭ» сертификатом является (например!) сам гамильтонов цикл — последовательность из n чисел, указывающая, в каком порядке следует проходить этот гамильтонов график.
Итак, он находится в классе NP. Очень похоже на так называемый класс NP. класс co-NP — совокупность задач о разрешимости, для которых ответ «нет» можно проверить за полиномиальное время при наличии дополнительной информации (так называемая задача контрпример ).
Например, для задачи о разрешимости «Вот число X, верно ли, что оно простоеЭ» контрпримером является делитель X, отличный от 1 и X. Это означает, что эта проблема лежит в классе ко-NP. Опять же, на каждое «нет» обязательно нужен контрпример.
А также есть класс П представляет собой совокупность всех задач разрешимости, которые можно решить за полиномиальное время.
Заметим, что формально P содержит именно задачи разрешимости, т.е.
вопрос «Сколько будет A+BЭ» там не место! (Он переходит в немного другую класс ФП ).
Но задачи такого рода всегда можно переформулировать в серию задач о разрешимости, добавив еще один параметр k: «Правда ли, что k-й бит выражения A+B равен 1Э» Делая серию таких запросов, мы, по сути, Полиномиальная редукция Кука вопрос «Сколько будет стоить А+ВЭ» к проблеме разрешимости.
Но об этом ниже.
Любая задача из класса P лежит в классе NP, поскольку ответ «да» можно проверить за полиномиальное время, используя вообще любой сертификат (например, сертификат « Клянусь своей мамой! ").
Алгоритм проверки следующий: выбросить сертификат и просто найти ответ на исходный вопрос с нуля за полиномиальное время.
По этой же причине любая задача из класса P также лежит в классе ко-NP. Еще раз о тонкостях принадлежности к классам.
Вопрос «Правда ли, что число X простоеЭ» принадлежит со-NP, а вопрос «Верно ли, что X — составное числоЭ» принадлежит НП.
В соответствии с алгоритм трех индейцев , на оба этих вопроса можно ответить за полиномиальное время.
Это означает, что оба этих вопроса, помимо всего прочего, относятся к классу П! Однако эти два вопроса имеют мало общего со следующими очень похожими вопросами.
вопрос «Какой наименьший делитель X больше 1Э» (которая не входит ни в NP, ни в co-NP, и никто не знает, как ответить за полиномиальное время (и за RSA-шифрование Это хорошо!)).
Те.
посмотрите, вопрос «Правда ли, что X — составное числоЭ» лежит в NP, так как для ответа «да» существует сертификат — делитель X между 1 и X, позволяющий за полиномиальное время проверить, что ответ действительно «да».
Но, благодаря алгоритму трёх индейцев, подходящий сертификат тоже есть» Клянусь своей мамой! ", то есть алгоритм, решающий задачу, не должен предоставлять сертификат, подтверждающий принадлежность проблемы к классу NP! Кстати, существуют задачи разрешимости, не принадлежащие P, NP или ко-NP. Например, классический проблема с выключением : «Учитывая программный код, правда ли, что он будет выполнен за конечное времяЭ» Но это совсем другая история.
Теперь о полиномиальной сводимости.
Существует несколько схем сведения проблем друг к другу.
По словам Карпа Задача U называется полиномиально сводимой к задаче V, если для любого входного сигнала u для задачи U мы можем за полиномиальное время преобразовать его во входной сигнал v для задачи V, передать его в V и получить ответ. (что означает «да» или «нет», помните?), что и будет ответом на исходную задачу U. По словам Кука , проблема U называется полиномиально сводимой к проблеме V, если существует алгоритм с полиномиальным временем, который решает проблему U, используя задачу V как оракул , т.е.
алгоритм может построить столько же (но полиномиального числа!) наборов входных данных для задачи V и найти ответ за одну итерацию.
Обе эти части информации показывают, что в определенном смысле проблема U не более сложна, чем проблема V. То есть, если мы можем решить V в каком-то смысле быстро, то мы также можем решить и U в каком-то смысле быстро.
И если мы не знаем, как быстро решить U в определенном смысле, то мы также не знаем, как быстро решить V в определенном смысле.
Таким образом, упомянутый выше вопрос «Сколько стоит А+ВЭ» не сложнее, чем вопрос «Верно ли, что k-й бит выражения A+B равен 1Э», и поскольку второй из них лежит в P, ответить на первый вопрос легко (за полиномиальное время!), хотя оно и не лежит в P. Фактически редукция по Карпу является частным случаем редукции по Куку, т.е.
в случае редукции Карпа оракул вызывается только один раз в самом конце и его ответ без каких-либо изменений считается ответом на исходный проблема.
Кроме того, в случае редукции Кука проблемы U и V не обязательно должны быть проблемами разрешимости.
Задача из класса NP называется NP-полный , если любая задача из класса NP (т. е.
вообще любая задача!) полиномиально сводима к ней.
Проблема выполнимости булевой формулы (SAT) — первая задача, для решения которой было проверенный NP-полнота явный смешивание любой проблемы от класса NP до SAT. Те.
SAT — это своего рода универсальное задание, которое, быть оракулом , позволяет быстрый решить любую задачу из класса NP. Позже выяснилось, что огромное количество других задач класса NP также являются NP-полными! Обычно это легко доказывается полиномиальной редукцией какой-либо другой NP-полной задачи (обычно SAT, возможно, через цепочку других задач) к этой.
Задача называется NP-сложной, если к ней можно свести любую NP-полную задачу.
Если эта NP-трудная задача также принадлежит к классу NP, то она, очевидно, является NP-полной задачей.
Примером NP-сложной задачи, не принадлежащей классу NP, является задача по упаковке контейнера «Каково наименьшее количество контейнеров, в которые можно упаковать все эти предметыЭ» поскольку к нему сводится NP-полный проблема деления «Можно ли разделить все эти предметы на две кучки одинакового общего весаЭ» Самый большой вопрос во всей этой демагогии заключается в следующем: решается ли какая-либо NP-полная задача за полиномиальное время? Если да, то P=NP и любую задачу из класса NP можно решить за полиномиальное время, и это очень хорошо для многих прикладных комбинаторных задач и очень плохо для некоторых алгоритмов шифрования.
Для формальности сформулируем задачу X и игру «Выращивание сакуры» как задачи разрешимости.
Проблема X: «Для кубического плоского 3-связного графа G верно ли, что он содержит гамильтонов циклЭ» Игра Growing Sakura: «Учитывая уровень из игры Growing Sakura, правда ли, что у него есть решениеЭ» Что ж, сведем NP-полную задачу X к игре «Растущая сакура».
Те.
На основе входных данных задачи X построим такой уровень «Растущая сакура», что его решение также даст ответ на исходную задачу X. Затем мы покажем, что задача X не сложнее игры «Выращивание сакуры».
Для этого нам понадобятся следующие структуры:
И-гаджет
Здесь все просто – ветка сакуры, идущая с любой из трех сторон, может расти дальше в обе стороны одновременно.
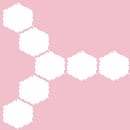
ИЛИ-гаджет
Для данного элемента ветка сакуры должна выбрать ровно одно направление из двух (на самом деле не более одного, но это действие бессмысленно).Второе направление придется освещать позже и с другой стороны.


ONE-WAY-гаджет
Эта конструкция представляет собой разновидность диода.Она позволяет ветке цветущей сакуры идти только в одном направлении.


Те.
в этом направлении проходит: 

Но этого нет: 
Я не смог придумать такую же конструкцию без дополнительных корневых точек, может быть, у вас получится?
LOCK-гаджет
Самый сложный элемент, его строительство заняло довольно много времени.


Суть этого элемента заключается в следующем.
Он имеет решения только в следующих конфигурациях:
А) 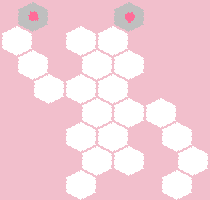
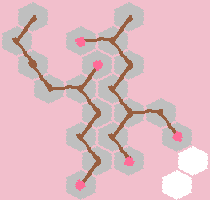
б) 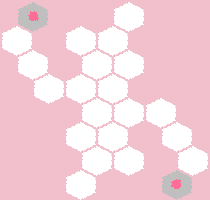

Однако в следующей конфигурации решений нет: 
Более того, вы даже не сможете закрыть ни один из крестов, не получив ситуацию «одинокой камеры».
Теперь давайте соберем все это вместе!
Из ОР-гаджетов уже можно в первом приближении собрать планарный кубический 3-связный граф.Но правила игры требуют, чтобы ребра, не входящие в гамильтонов цикл, были покрыты.
И чтобы это обеспечить, нужна более громоздкая конструкция.
Вот она: 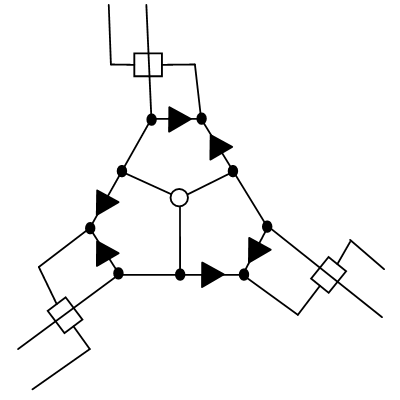
Эта конструкция соответствует одной вершине в нашем кубическом графе.
Давайте теперь посмотрим, как это работает. Не ограничивая общности, пусть ветка сакуры идет снизу слева (по двум путям сразу).
Затем будет рассмотрена следующая часть схемы: 
Теперь, в зависимости от того, какой из двух вариантов мы выберем, мы получим следующее развитие событий: 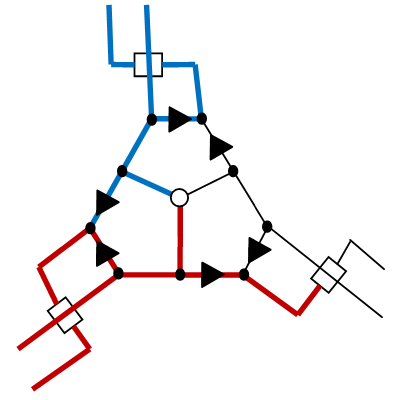
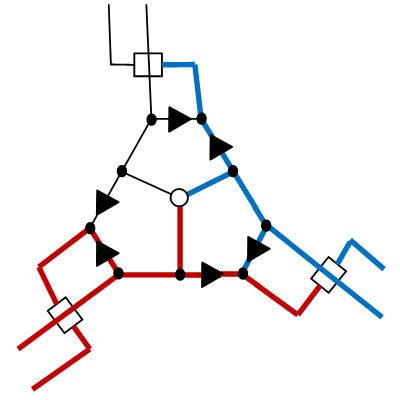
Обратите внимание, что в обоих случаях мы направили две ветки сакуры в одну сторону и ровно одну из них в другую.
Те.
Мы раскрасили ребро графа в одну сторону, но не в другую.
Теперь, когда наш гамильтонов путь достигнет той вершины в графе, где мы сейчас не раскрасили ребро, оттуда пойдет еще одна ветвь (отмечена внизу зеленым цветом), которая разблокирует гаджет LOCK и закроет все, что нужно закрыть: 

Случаи, когда мы пришли к вершине, для которой одна или две соседние вершины уже были посещены нашим путем, читателю предлагается проанализировать самостоятельно.
Ну а теперь просто построим огромный уровень для всего плоского кубического 3-связного графа и проверим, есть ли у него решение.
Если есть, то восстановить цикл для исходного графа несложно — достаточно посмотреть, как растет ветка сакуры в ИЛИ-гаджетах (хотя формально восстанавливать ее явно не требуется).
Построить такой уровень всегда можно – все гаджеты можно вращать и соединять цепочкой ячеек достаточной длины.
Поскольку граф изначально планарен, нет необходимости решать задачу о пересечении путей.
Казалось бы, все доказано? Нет, они этого не доказали.
Построенный уровень вообще не будет иметь решения – мы не запустили процесс «цепной реакции» – гамильтонову пути некуда начинать.
Это можно решить очень просто.
Берём любое ребро (а точнее соответствующий гаджет ЗАМОК) и делаем так: 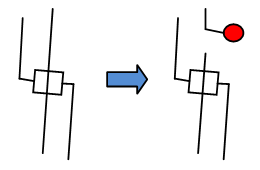
Красный круг — это место, где мы начинаем выращивать нашу ветку.
И нам обязательно нужно прикрыть обломанный конец, чтобы гамильтонов цикл замкнулся! Сейчас это доказано? Нет! Внезапно в графе появляется гамильтонов цикл, который Нет проходит по тому краю, с которого мы начали его искать! Что делать? Нужно попробовать поискать цикл, начинающийся с другого края.
Очевидно, что для любых двух ребер, выходящих из одной вершины, хотя бы одно из них будет иметь искомый гамильтонов путь, если он существует. Следовательно, для решения задачи Х вам понадобится не более двух уровней Выращивания Сакуры.
"Позволь мне!" — скажете вы, — «чуть выше было написано, что мы решим только один уровень игры «Растущая Сакура», эквивалентный графу в задаче Х!» Правильно, я вас нагло обманул! Однако это не портит доказательство Теги: #ludum Dare #выращивание сакуры #NP #np-hard #NP-Complete #Разработка игр #Алгоритмы #математика

-
Шеллинг, Фридрих Вильгельм Йозеф
19 Oct, 24 -
Конфиденциальность В Интернете: P3P
19 Oct, 24 -
Социальные Сети Как Новые Медиа
19 Oct, 24


