Привет.
Наверняка каждый был свидетелем визуальной оценки степени сходства ребенка с родителями: что-то вроде «он похож на папу, но и на маму похож!!!» 
( взято отсюда )
Как и в примере на изображении, степень сходства можно оценить в процентах.
Вы также можете использовать родственников для более точного описания лица ребенка в виде взвешенной суммы лиц родственников.
И это будет выглядеть и восприниматься вполне естественно для «обычного» человека, не связанного с антропологией или, например, криминологией.
Для профессионала в области анализа и распознавания лиц человеческое лицо предстает скорее как набор параметров.
То есть точка (набор координат) в некотором пространстве с базисом (осями, соответствующими параметрам).
А если описать лицо ребенка в сравнении с его родственниками, то, скорее всего, точка, соответствующая лицу ребенка, будет находиться в этом пространстве параметров внутри выпуклой оболочки облака точек, соответствующих лицам ближайших родственников (но это не уверен).
Собственно, о чём я.
этим двум подходам к описанию лиц соответствуют две системы координат:
- барицентрический — описание точки пространства (в нашем примере: лица) через взвешенную смесь других точек;
- аффинное — описание точки пространства через координаты в некотором базисе.
Так что же такое барицентрические координаты?
Впустить-мерное пространство дано
точка

с радиусами-векторами
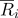
,
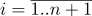
.
При этом ни одна из точек не лежит в линейной оболочке радиус-векторов остальных точек.
Проще говоря, совсем просто: пусть эти точки образуют фигуру, которую невозможно полностью представить в пространстве размерностью меньше
.
В случае одномерного пространства (линии) нам нужны 2 несовпадающие точки, в случае двумерного пространства - невырожденный треугольник, в случае трехмерного пространства - тетраэдр.
Тогда любая точка пространства 
может быть представлено радиус-вектором 
: 
Набор 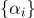
и есть барицентрические координаты.
Почему барицентрические координаты лучше/хуже аффинных?
Начнем с относительных недостатков:- в барицентрическом представлении нам понадобится на одну координату больше, чем в аффинном;
- расстояние между точками, определенными барицентрически, не может быть напрямую рассчитано в этих координатах.
барицентрические координаты при описании точки в
В -мерном пространстве число степеней не увеличивается.
Барицентрические координаты, определенные в формуле (1), связаны соотношением: 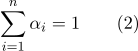
Что касается второго недостатка, то если есть необходимость вычислить расстояние между точками, представленными барицентрически, то имеет смысл вычислять скалярные произведения.
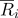
и использовать аналог расстояния Махаланобиса.
Какие бонусы дает использование барицентрических координат?
- Барицентрические координаты инвариантны к аффинным преобразованиям пространства.
Это свойство используется, например, для линейной интерполяции в компьютерной графике.
Пусть текстурные координаты заданы в вершинах треугольного элемента поверхности
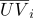
и нормальные люди
(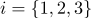
), то каждая точка этой площади поверхности будет иметь барицентрические координаты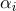
, его текстурные координаты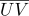
и нормальный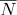
можно рассчитать как: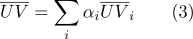
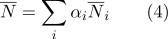
- Используя барицентрические координаты, легко определить, принадлежит ли точка

часть пространства, ограниченная многогранником с вершинами
: Это выполняется только в том случае, если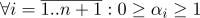
.Равенство i-й барицентрической координаты 1 означает, что точка
совпадает с
.Если несколько барицентрических координат равны 0, то это означает, что точка принадлежит подпространству, натянутому радиусами-векторами остальных точек, соответствующие координаты которых больше 0.
Должно быть, их очень сложно вычислить?
Не сложнее любого линейного преобразования системы координат. Потому что, по сути, именно таким преобразованием является вычисление барицентрических координат. Перепишем радиус-вектор точек в следующем виде: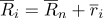
, Где
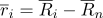
— радиус-вектор в системе координат с центром в точке
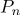
.
Тогда формулу (1) можно переписать следующим образом: 
Давайте раскроем скобки, чтобы подвести итог: 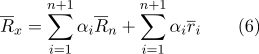
По свойствам (2): 
Соответственно:
,
Где
Учитывая (2), ограничимся вычислением первых n барицентрических координат. Представим себе переход к барицентрическим координатам как линейное преобразование:
,
Где
— вектор из n барицентрических координат (кроме последней),
— матрица преобразования.
Учитывая свойства барицентрического представления, если
заменить один из векторов
(
), то мы получим вектор с нулевыми компонентами, кроме i-й, которая будет равна 1.
Если матрица
умножить на матрицу
, составленный из столбцов
, то мы должны получить единичную матрицу (матрицу с единицами на главной диагонали и нулями в остальных элементах):
,
Где
,
- единичная матрица (
— Символ Кронекера: 1, если
, в противном случае — 0).
Из (10) находим
:
Таким образом, имея набор точек с радиусами-векторами 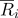
, 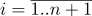
мы можем вычислить матрицу для преобразования в барицентрические координаты:
Используя эту матрицу, мы можем получить первое
барицентрические координаты точки
с радиус-вектором
:
Снова воспользовавшись соотношением (2), получим последнюю барицентрическую координату:
Заключение
На первый взгляд барицентрика может показаться неуклюжей и сложной.Но на самом деле это очень удобный и незаменимый инструмент для многих задач, к которому быстро привыкаешь.
Потому что никакой магии здесь нет, это линейная алгебра в чистом виде! Теги: #python #математика #Алгоритмы #Numpy #математика на пальцах #матрица перехода #системы координат #инвариант

-
Они Смотрят За Тобой Онлайн?
19 Oct, 24 -
Ваше Отношение К Домену Www
19 Oct, 24 -
Сегалович Хвалит Nigma.ru
19 Oct, 24


