Есть загадочный факт о линейных преобразованиях: некоторые из них, а именно неоднородное масштабирование и сдвиг, по какой-то причине различают «обычные» векторы и нормали.
Когда мы преобразуем «обычный» вектор с помощью матрицы, то нормали по какой-то причине необходимо преобразовать с помощью обратной транспонированной матрицы.
Как это понимать? Используя простые расчеты можно убедиться, что обратная транспонированная матрица сохраняет перпендикулярность нормалей к своим касательным плоскостям.
В какой-то степени этих доказательств достаточно, но они упускают из виду более глубокую и интересную историю о геометрии, стоящей за всем этим.
Именно эту историю я хочу рассказать в следующих нескольких статьях.
Единицы измерения и масштабирование Вот небольшой вводный курс, прежде чем мы углубимся в суть статьи.
Давайте рассмотрим старый добрый однородный масштабирование (один коэффициент по всем осям).
Трудно придумать более безобидное преобразование — это просто умножение всех векторов на одно и то же число.
Но при ближайшем рассмотрении здесь происходит нечто не совсем тривиальное.
Некоторые величины несут в себе физические «размеры» или «единицы», такие как длины, площади и объемы.
При масштабировании эти величины изменяются в соответствии со своими единицами измерения.
Некоторые значения вообще «безразмерны» и не изменяются при масштабировании.
В качестве примера перечислим все возможное поведение юнитов при масштабировании в трехмерном пространстве.
Обозначим масштабный коэффициент как
.
Затем:
- Безразмерные числа не изменяются, то есть умножаются на
. - Длина умножается на
. - Квадраты умножается на
. - Объемы умножается на
.Но это еще не все: есть еще плотность , которые изменяются обратно пропорционально масштабному коэффициенту:
- Линейные плотности умножается на
. - Плотность по площади умножается на
. - Объемная плотность умножается на
.Плотности могут выражать такие вещи, как количество текселей на длину, геометрическую вероятность или количество частиц в объеме.
Если 3D-модель масштабирована вбок увеличивать , а размер текстуры не меняется, то и плотность текселей на ней уменьшается , и так далее.
А именно, им соответствуют различные степени длины от -3 до 3. Значение, соответствующее
-я степень длины, масштабированная как
.
(Можно получить величины с масштабирующими степенями
и более, или даже с дробными степенями.
Но оставим их за рамками рассмотрения, поскольку они не имеют хорошей геометрической интерпретации в 3D.) Ладно, возможно, это чем-то похоже на разницу между обычными векторами и нормалями.
Но как это работает для векторных величин? Как неоднородное масштабирование влияет на всю эту картину? И причем здесь обратная транспозиция? Чтобы по-настоящему понять это, нам придется углубиться в математику еще дальше.
Внешняя алгебра С этого момента и до конца нам понадобится внешняя алгебра , или алгебра Грассмана.
Поскольку не все читатели, скорее всего, с ними знакомы, я кратко введу эту тему.
Для более глубокого понимания, пожалуйста, обратитесь к эта лекция Рика Лангиела или первых глав книги Дорста Геометрическая алгебра для информатики .
В Интернете есть множество других материалов.
Внешняя алгебра — это расширение линейной алгебры, которое работает не только с векторами, но и с некоторыми геометрическими объектами более высокого порядка, называемыми бивекторы , тривекторы и так далее.
В целом эти объекты называются
-векторы , Где
— внешняя степень или размер объекта.
Они следуют тем же правилам, что и векторы: их можно складывать и умножать на скаляры.
Но их геометрический смысл различен.
Мы часто думаем о векторе как об абстрактной стрелке — он имеет направление в пространстве (куда указывает стрелка) и абсолютное значение, представленное длиной стрелки.
Бивектор во многом аналогичен, но он плоский , не линейный.
Он представлен не стрелкой, а абстрактным участком плоской поверхности.
Как и векторы, бивекторы также имеют направление в том смысле, что плоскость может быть обращена в разные стороны в пространстве.
Они также имеют абсолютную величину, геометрически представленную как квадрат секция самолета.
Чего у них нет, так это концепции формы на поверхности.
Визуализируя бивектор как часть плоскости, вы можете думать о нем как о квадрате, круге, параллелограмме или любой другой произвольно сложной фигуре соответствующей площади.

Точно так же тривекторы — это трехмерные векторные величины, которые представляют собой область пространства, а не плоскость или стрелку.
Опять же, они не имеют определенной формы, а имеют лишь абсолютную ценность, которая теперь объем , а не площадь или длина.
В трехмерном пространстве тривекторы не имеют направления в полезном смысле этого слова.
Другими словами, у них есть только одно возможное направление: параллельно пространству .
Однако тривекторы имеют два противоположных направления, которые мы можем назвать «положительным» и «отрицательным» или «правосторонним» и «левым».
Это похоже на то, как вектор может указывать влево или вправо на одномерной линии, и мы можем называть эти направления положительными и отрицательными, если захотим.
В пространствах более высоких измерений тривекторы также могут иметь множество разных направлений, как векторы и бивекторы.
Кроме того, могут существовать квадровекторы и
-векторы высших степеней.
Трех измерений нам будет достаточно.
Базовый

-векторы
Бивекторы и тривекторы можно разложить на составляющие в базисе так же, как это делается с обычными векторами.
Обозначение векторных координат
, Значит это
можно представить в виде линейной комбинации базисных векторов:
Базисные векторы
,
,
определить направление и масштаб осей
,
,
.
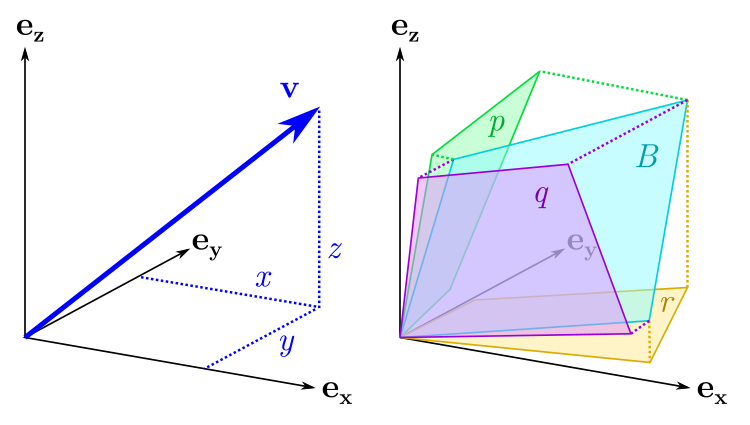
Аналогично, бивектор
можно представить линейной комбинацией базисные бивекторы :
Здесь
представляет собой бивектор единичной площади, ориентированный вдоль плоскости
.
И
можно представить по аналогии.
Базисные бивекторы соответствуют не координатным осям, а плоскостям, охватываемым пары топоры.
Так определяются «бивекторные координаты»
, с помощью которого мы можем обозначить или построить любой бивектор в пространстве.
Случай с тривектором менее интересен:
Как мы отмечали выше, тривектор в 3D имеет только одно возможное направление, поэтому у него есть только один базовый элемент: единичный тривектор «вдоль» пространства.
.
Все остальные тривекторы являются продуктами
скаляру.
Внешняя работа
Итак, внешняя алгебра содержит различные вектороподобные объекты разных степеней: обычные векторы (степень 1), бивекторы (степень 2) и тривекторы (степень 3).
Скалярам можно присвоить степень 0. Наконец, чтобы объекты разных степеней могли взаимодействовать, внешняя алгебра определяет операцию, называемую внешняя работа , обозначенный
.
Он позволяет построить бивектор путем умножения двух векторов, например:
В общем, можно перемножить любые два вектора и получить бивектор, лежащий в плоскости, определяемой этими векторами.
Абсолютной величиной бивектора будет площадь параллелограмма, построенного на этих векторах (как векторное произведение).
Обратите внимание, что бивектор не «помнит», какой именно конкретно оно строится в двух векторах.
Любые два вектора в одной плоскости, определяющие параллелограмм той же плоскости и ориентации, будут давать один и тот же бивектор.
Бивектор можно разложить на векторы, но не единственным способом.
Вы также можете умножить три вектор или бивектор с вектором, чтобы получить тривектор.
Такое произведение эквивалентно «скалярному смешанному произведению», которое дает тривектор, представляющий ориентированный объем параллелепипеда, натянутого на три вектора.
Внешний продукт подчиняется большинству известных правил умножения, таких как ассоциативность и закон распределения.
С ним также можно сочетать умножение на скаляр.
Для скаляра
мы получаем:
Но внешнее произведение двух векторов антикоммутативный , опять же, как перекрестное произведение.
Для векторов
у нас есть:
Отсюда следует несколько выводов.
Во-первых, внешнее произведение любого вектора на самого себя равно нулю:
.
При этом внешнее произведение множества линейно зависимый векторов также равно нулю.
Например,
Когда
И
коллинеарный.
В случае трёх векторов
Когда
копланарный.
Это также объясняет, почему степени выше 3 не существуют в трехмерном пространстве.
Внешняя работа четыре трехмерных векторов всегда равна нулю, поскольку в трехмерном пространстве не может быть четырех линейно независимых векторов.
Преобразования
-векторы Ранее я заявил, что абсолютное значение вектора можно представить как длину, значение бивектора как площадь, а значение тривектора как объем.
Но что именно управляет этим сравнением единиц с количествами? Выше мы видели, что длины, площади и объемы ведут себя по-разному при масштабировании.
Равномерное масштабирование трехмерного пространства с коэффициентом
будет масштабировать длины, площади и объемы как
соответственно.
Теперь у нас есть аппарат, показывающий, что векторы, бивекторы и тривекторы ведут себя совершенно одинаково.
Вы можете применить масштаб к вектору, умножив его на подходящую матрицу:
Вектор
в целом, его составляющие
, и его скалярное абсолютное значение умножаются на коэффициент
при масштабировании, поэтому мы можем назвать это длиной, и противоречия не будет. А как насчет бивекторов? Чтобы увидеть, как они ведут себя при масштабировании (или любом другом линейном преобразовании), давайте посмотрим на внешний продукт. В трехмерном пространстве любой бивектор можно разложить во внешнее произведение двух векторов.
Мы знаем, как преобразовывать векторы, а это значит, что мы можем преобразовать бивектор, преобразовав составляющие его векторы и взяв внешнее произведение результатов:
Ух ты! Поскольку бивектор состоит из двух факторов, каждый из которых масштабируется на
, бивектор приобретает коэффициент
, что делает его областью.
Тривекторы также можно преобразовать, разложив их на векторы.
Теперь неудивительно, что три векторных множителя дают тривектору коэффициент
.
Вот расчеты на полноту:
Бивекторы и неоднородный масштаб
Теперь мы можем, наконец, вернуться к исходному вопросу.Что станет сложнее, если мы подадим заявку неровный масштабирование? Чтобы понять это, давайте посмотрим на пример.
Масштабируем в 3 раза по оси
, оставляя остальные оси неизменными.
Вы получите матрицу вида:
На обычных векторах его действие очевидно: компонента
умноженное на 3, и компоненты
Не менять.
В общем, матрица меняет как длину, так и направление вектора в зависимости от исходного направления: векторы, близкие к оси
тянуться сильнее, а те, кто ближе к плоскости
- слабее.

Как такое преобразование повлияет на бивектор? Во-первых, давайте пойдем со стороны геометрии.
Бивектором обозначается участок плоскости заданной площади и направления, в котором направлена «лицевая» сторона.
При растяжении такого сечения вдоль оси
мы ожидаем, что и направление, и площадь изменятся.
Но разные бивекторы изменятся по-разному: на бивектор, близкий к плоскости
, растяжение повлияет меньше, а бивектор, плоскость которого близка к
, будет растянуто больше.

Хорошо, вернемся к алгебре.
Как показано выше, любой бивектор можно разложить на осевые базисные бивекторы:
Чтобы применить масштабирование
к бивектору, вам просто нужно применить его к базисным бивекторам.
Для этого разложим их на базисные векторы и применим
им:
Это соответствует геометрической интуиции:
не изменился, но
И
получили коэффициент 3, поскольку их плоскости включают ось
.
Итак, вот общий эффект от применения
к бивектору
:
Теперь, как и в случае с вектором, можно расписать преобразование бивектора
в виде компонентов, к которым применена матрица:
Это то же самое преобразование, которое мы только что получили, но записанное в других обозначениях.
Обратите внимание на одно отличие: матрица в этом выражении имеет вид не совпадает с матрицей
оригинальная трансформация.
Отметим, однако, забавное совпадение: обратное транспонирование
пропорциональна матрице из предыдущей формулы:
Для чего это?
Сопряженная матрица
Фактически, матрица преобразования бивектора имеет вид присоединенная матрица К.
Она пропорциональна обратной транспонированной матрице с коэффициентом
.
(Вернуться к
матрицу можно получить транспонирование сопряженной матрицы , разделив его на
).
Сопряженная матрица определена даже тогда, когда
необратимый.
Это хорошее свойство, потому что мы можем преобразовать вектор в необратимую матрицу, и то же самое должно быть возможно сделать и с бивектором! Давайте лучше разберемся, зачем нам сопряженная матрица.
Введем понятие алгебраического дополнения.
Каждый элемент квадратной матрицы
существует алгебраическое дополнение.
Алгебраическое дополнение элемента на
-я строка и
столбец следующим образом:
- Возьмем исходную матрицу
и зачеркни строку
и столбец
.Будет подматрица размера
. - Вычислим определитель этой подматрицы.
- Умножим определитель на
, то есть меняем его знак, если
странный.Это алгебраическое сложение!
, в результате чего присоединенная матрица .
Но почему эта конструкция работает при бивекторном преобразовании? Давайте посмотрим на первую компоненту бивектора
.
Этот член представляет собой плоскую составляющую Теги: #Разработка игр #математика #Работа с 3D-графикой #нормали #внешняя алгебра #бивекторы
-
Почему Я Выбираю Erp В Качестве Карьеры?
19 Oct, 24 -
Графический Дизайн Как Все О Творчестве
19 Oct, 24 -
Формула Успешного Интернет-Маркетинга
19 Oct, 24 -
Как Купить Linux Vps Сервер
19 Oct, 24 -
Повышение Качества Управления Проектами
19 Oct, 24 -
«Аска» - Нормальный
19 Oct, 24


