Невероятные Приключения Роберта Хэнбери Брауна И Ричарда Твисса. Часть 3: От Телескопа К Квантовым Вычислениям

Концовка.

Начало здесь: часть 1 , часть 2 .

По-английски о сложных и непонятных вещах говорят «ракетостроение».

В русском языке часто прибегают к сравнению с теорией относительности или квантовой механикой.

Хотя последнее начинается с очень простых идей: скажем, с того, что свет распространяется отдельными частицами — фотонами.

За секунду вы можете увидеть 96, 97 или 99 фотонов, но никогда — 99 с половиной.

Эта удивительно простая идея приводит к весьма необычным последствиям.

До наведите двойной телескоп на Сириус , наши герои решили проверить это в лаборатории.

Роль звезды играл свет лампы, сфокусированный на небольшое отверстие, а вместо двух телескопов использовались два фотоумножителя.

Разместить их рядом было невозможно, поэтому придумали хитрость: свет от «звезды» направлялся на полупрозрачное зеркало, которое отражало одну половину излучения и пропускало другую.

Один фотоумножитель смотрел на отражение «звезды», второй стоял за зеркалом и видел «звезду» в свете:



Эксперимент показал, что теория Твисса была верна: чем больше были «раздвинуты» трубки фотоумножителей, тем меньше была измеренная корреляция.

Но здесь возникает интересный вопрос.

Фотоумножитель — очень чувствительный фотодетектор; его основная задача — генерировать мощный импульс тока для одного прилетевшего фотона: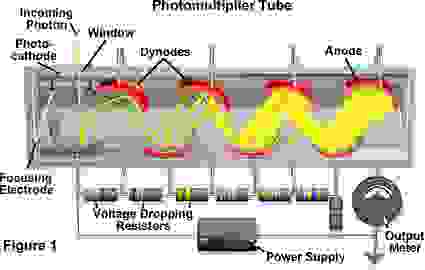



Фотоумножитель.

Фотон прибыл сверху слева и породил электрон.

Он ускорялся полем, ударялся о динод (промежуточный анод) и выбивал из него два электрона.

Эти два электрона также ускорились и выбили четыре электрона из следующего динода и так далее.

В результате одиночный фотон генерировал хороший импульс тока.

Фотоумножитель видит не свет, а отдельные фотоны.

Это логично: ведь интенсивность света — это просто количество фотонов, прилетающих в секунду.

Но тогда корреляцию надо рассчитывать не для зашумленного сигнала, а для фотонов.

Разумно, почему бы и нет? Давайте просто заменим интенсивность( я ) по числу фотонов ( н ):



Для независимых источников корреляция равна единице.

Это логично: это случай разнесенных телескопов, когда они видят разные части звезды.

Но когда телескопы «смещаются», корреляция становится равной двум.

Это значит, что фотоны приходят не по отдельности, а парами! Как же так?



Пришло время вспомнить фундаментальное свойство квантовой оптики: за любой интервал времени всегда приходит целое число фотонов.

На основе этого свойства Рой Глаубер из Гарварда создает теория когерентности , описывающее свойства фотонов, их статистику, когерентность и всё такое.

Он основан на методе вторичного квантования, в котором используется операторы рождения и уничтожения фотонов – названия говорят сами за себя: фотоны появляются и исчезают по отдельности, а их общее количество всегда остаётся целым числом.

Теория когерентности Глаубера подробно описала эксперимент Хэнбери Брауна-Твисса и показала, что фотоны от звезды (да и от любого другого теплового источника — лампы, светодиода, газового разряда и т. д.) действительно «стараются» прийти парами.

«та же теория объяснила физический смысл этой загадочной корреляционной функции g ⁽²⁾ : показывает, насколько «дружелюбен» источник излучает фотоны.

Если г ⁽²⁾ больше единицы, то фотоны предпочитают излучаться группами; если меньше единицы, то отдельно.

Ну г ⁽²⁾ = 1 соответствует фотонам, излучаемым независимо.

Как ни странно, лазер тоже генерирует свет с g ⁽²⁾ = 1.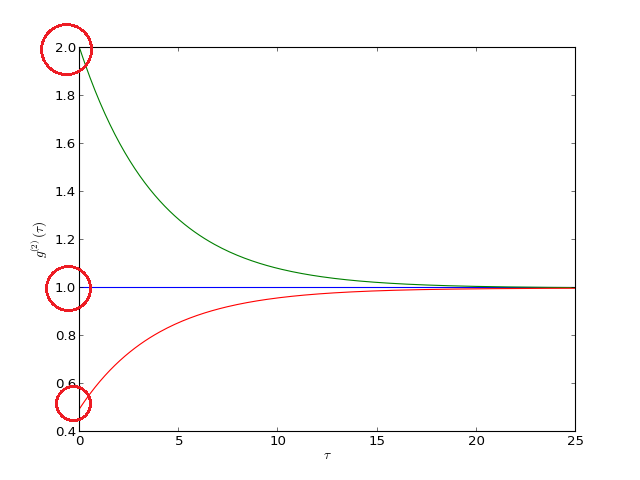



Круги показывают разные значения g. ⁽²⁾ для «сдвинутых» телескопов.

Для «расширенного» g ⁽²⁾ всегда равен единице (справа).

Как и ожидалось, г ⁽²⁾ = 2 означает, что фотоны приходят парами и эксперимент верен.

Семья Хэнбери Браун отпраздновала это радостное событие рождением двух близнецов.

Роберт Хэнбери Браун явно доволен происходящим.

Я говорил о теории когерентности и магии двойных фотонов, но получилось как-то непонятно.

К счастью, теория имеет более наглядное описание.

Если источник излучает в среднем 22,5 фотона в секунду, то каждую секунду мы, скорее всего, будем обнаруживать 22 или 23 фотона, реже 15 или 30 и почти никогда – ноль или сотню.

Надвигающийся Распределение числа фотонов с максимумом в 22,5:



Насколько он широкий? Оказывается, что «хорошее» излучение (если фотоны испускаются независимо друг от друга) с центром в N имеет ширину распределения, равную корню из N. Такое распределение называется Пуассон .

Если распределение шире, его называют суперпуассон (и более узкий субпуассоновский ):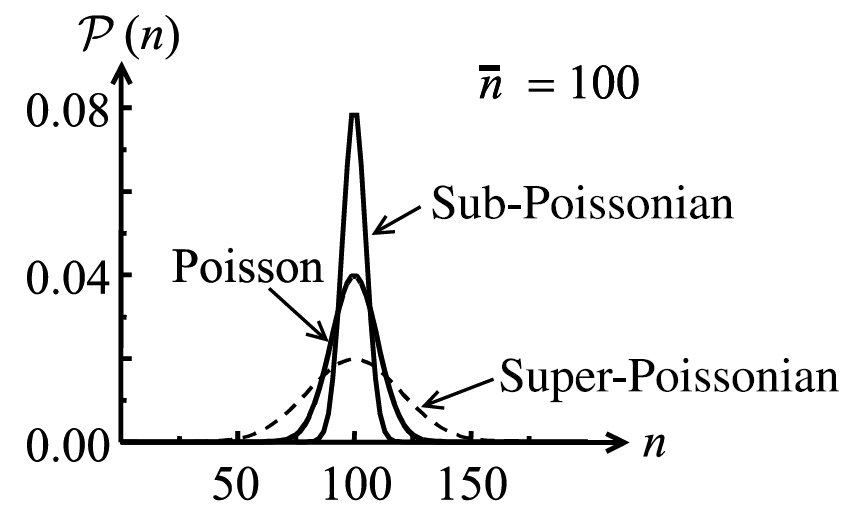



Пуассоновская, субпуассоновская и суперпуассоновская статистика.

Итак, функция g ⁽²⁾ показывает ширину распределения: чем она больше, тем шире распределение.

г ⁽²⁾ = 1 соответствует распределению Пуассона и не зависит от среднего числа фотонов.

То есть для любого лазера – как слабого, так и мощного – g ⁽²⁾ равен единице.

Для теплового света g ⁽²⁾ = 2. Означает ли это, что распределение в два раза шире лазерного? Не совсем.

Он шире лазерного, но выглядит совершенно иначе: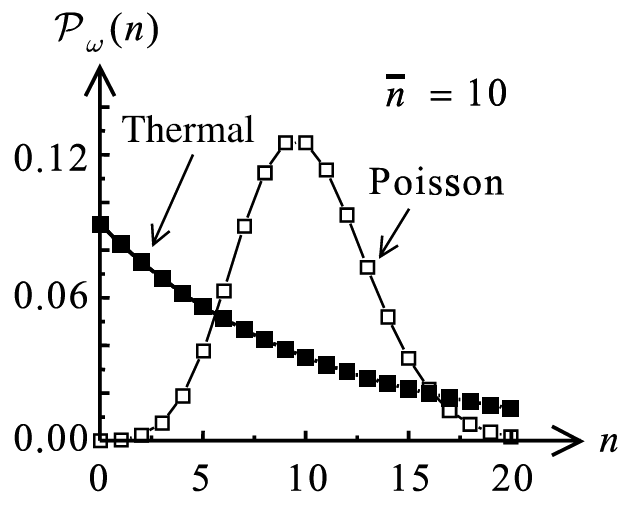



То есть тепловое излучение чем-то похоже на распределение энергетических уровней: чем выше уровень (чем больше фотонов), тем меньше вероятность его увидеть.

Вот главный вывод: тепловое и когерентное излучение имеют принципиально разные статистические свойства .

Самое приятное то, что измерение g ⁽²⁾ использование эксперимента Хэнбери Брауна-Твисса позволяет нам легко измерить эту статистику.

Где это применяется? Ну, например, при разработке лазеров: с помощью g ⁽²⁾ можно определить порог генерации (т. е.

условия, при которых излучение из теплового становится лазерным).

Ну и самый интересный (и полезный) случай — это g ⁽²⁾ = 0. Ширина распределения фотонов оказывается равной нулю! Что это значит? Оказывается, количество фотонов строго фиксировано и не меняется от секунды к секунде.

Распределение состоит из одного пика (правое изображение):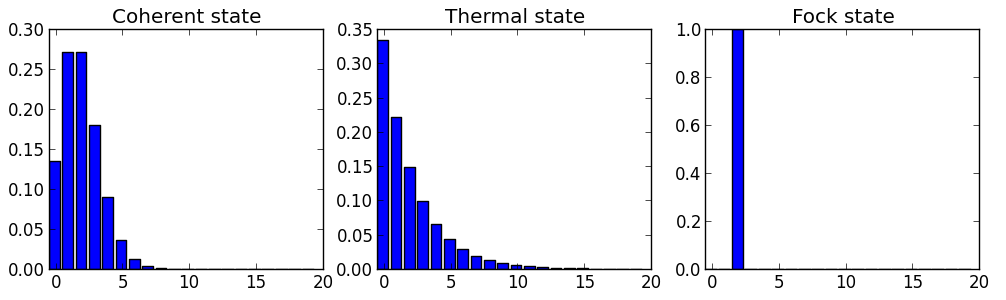



Статистика фотонов: Пуассона (также известная как когерентная, g ⁽²⁾ = 1), термический (г ⁽²⁾ = 2), Фока (он же N-фотон, g ⁽²⁾ = 0).

Самое интересное происходит, когда источник излучает ровно один фотон (в шапке написано, что такая штука называется источник одиночных фотонов ).

Такие устройства нужны для работы оптических транзисторов, переключения кубитов, квантовой криптографии и подобных приложений.

Требования к ним очень серьезные: они ни при каких обстоятельствах не должны генерировать более одного фотона.

В противном случае случайно испущенный фотон может привести к утечке информации.

Или, например, оптический переключатель включится от первого фотона и сразу выключится от второго.

Поэтому источники одиночных фотонов должны быть тщательно проверены.

Как обнаружить один фотон (а еще лучше два)? Обычный фотодиод бесполезен: отклик будет слишком слабым.

Использовать лавинный диод - но у него есть свои недостатки.

Например, у него есть мертвое время : на каждый прилетающий фотон генерирует длинный импульс тока, а в это время прилетает второй фотон, диод его просто не замечает:



Красная штриховка – мертвое время.

Обычно оно составляет не менее 100 пикосекунд. На помощь приходит идея наших главных героев: давайте осветим полупрозрачное зеркало и два детектора, а затем вычислим значение g. ⁽²⁾ .

Если г ⁽²⁾ = 0, то источник однофотонный, если g ⁽²⁾ > 0, то иногда он излучает два фотона.

А теперь – внимание, физическая магия! - весь три объяснения, почему это работает: 1. Из картинки с раздачами.

Если каждую секунду источник излучает один фотон, то в гистограмме один столбец приходится на «1», ширина распределения равна нулю и g ⁽²⁾ = 0. Если иногда испускается 2 фотона, то на гистограмме появляется столбец под цифрой «2» и ширина распределения растет, а вместе с ней растет и g ⁽²⁾ .

2. Из формулы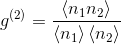



Если источник однофотонный, то n1 + n2 = 1, а значит одно из чисел равно нулю, а значит, произведение n1 и n2 также равно нулю, как и g ⁽²⁾ .

Если было испущено два фотона (n1 + n2 = 2), то, возможно, n1 = n2 = n1*n2 = 1, и g ⁽²⁾ становится больше нуля.

3. И, наконец, самое главное: здравый смысл! Если фотоны излучаются парами, то время от времени один фотон попадает в один диод, а второй – во второй.

Тогда мы увидим синхронную работу диодов — совпадения , которые увеличивают значение g ⁽²⁾ .

Если источник действительно однофотонный, то диоды никогда не сработают одновременно.

Идея Хэнбери Брауна–Твисса оказывается совершенно незаменимой при анализе однофотонных источников.

Для хорошего источника корреляционная функция g ⁽²⁾ выглядит примерно так:



Здесь ноль не слева, а посередине; влево — отрицательные смещения одного из детекторов (как если бы левый телескоп находился правее правого).

Главное остается прежним: с нулевой задержкой g ⁽²⁾ достигает нуля с очень большой задержкой, фотоны испускаются независимо и g ⁽²⁾ = 1. Не очень хороший источник выглядит примерно так: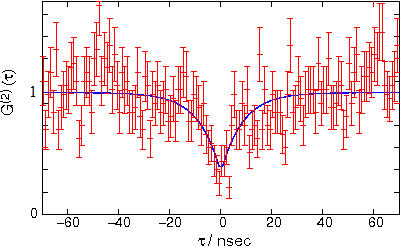



Видно, что функция не опускается ниже 0,4. Это означает, что источник часто излучает пары фотонов, и для особо важных приложений лучше поискать другой.

Рой Глаубер получил Нобелевскую премию по теории когерентности в 2005 году.

Наши главные герои не смогли ее разделить: Ричард Твисс не дожил до этого момента всего шесть месяцев; тремя годами ранее умер Роберт Хэнбери Браун.

Но, как известно, самое большое признание – это когда твое имя становится нарицательным.

Простая и гениальная идея – измерение корреляций с помощью стеклянной пластинки и двух диодов – осталась в истории под названием Трасса Хэнбери Браун – Твисс .

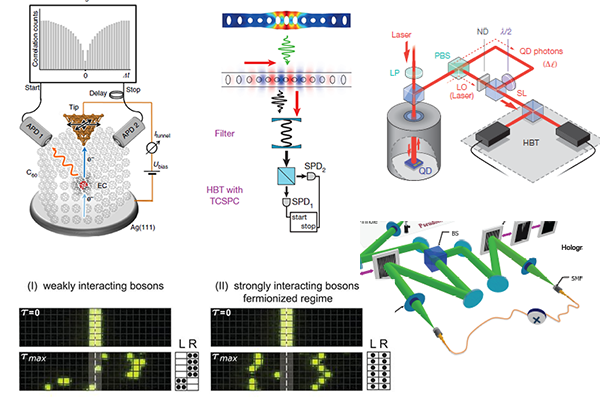
Фотографии из статей 2015 года в ведущих научных журналах Nature и Science, измеряющих корреляции с использованием схемы Хэнбери Брауна-Твисса.

Задача наблюдения: найти его в пяти местах :).

На этом история заканчивается, но можно найти ее логическое продолжение.

Здесь.

Источники М.

Фокс.

Квантовая оптика: Введение – Издательство Оксфордского университета, 2006. Р.

Хэнбери Браун.

Интерферометр интенсивности.

Его применение в астрономии.

– Лондон: Тейлор и Фрэнсис, 1974. Р.

Хэнбери Браун.

Боффин: личная история первых дней развития радара, радиоастрономии и квантовой оптики – Бристоль: Адам Хилгер, 1991. Некролог: Роберт Хэнбери Браун.

Природа 416, 34 (2002).

Изображений: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 .

Теги: #Популярная наука #лазеры #физика #оптика #история науки #история науки #невероятные приключения #корреляции

• Как Отображать Rss-Каналы На Вашем Сайте.

  19 Oct, 24

• Канн, Диего

  19 Oct, 24

• С Днем Фрилансера!

  19 Oct, 24

• Песочница В Windows

  19 Oct, 24

• Direct3D Vs Opengl: История Противостояния

  19 Oct, 24

• Беспроводная Клавиатура Logitech Для Wii

  19 Oct, 24

• Загрузка Исторических Данных В Sap С Помощью Lsmw — Написание «Макроса»

  19 Oct, 24

• Продолжение Темы Про Seagate Barracuda 7200.11.

  19 Oct, 24

• Вся Подборка It-Скидок Черная Пятница + Киберпонедельник В Одном Посте... И Пусть Никто Не Уйдет Обиженным

  19 Oct, 24

• Спринтерский Пульс: Построение Эффективной Работы В Большой Команде

  19 Oct, 24