Привет, Хабр! Сегодня я хочу поговорить о периодограмме и одном из возможных ее применений в области анализа временных рядов.
С его помощью можно определить, насколько хорошо идентифицированы постоянная, сезонная и случайная составляющие, а также сделать общие выводы о структуре временного ряда.
В этой статье я предлагаю посмотреть, как строится периодограмма, и проанализировать модельные и реальные примеры.
Кому интересно - добро пожаловать под кат.
Немного теории
Временной ряд – это данные, измеренные последовательно через определенные, чаще всего равные, промежутки времени.В классическом случае предполагается, что временной ряд состоит из трех составляющих: трендовой (T_n), сезонной (S_n) и случайной (E_n).
Классические модели временных рядов: 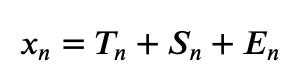
в аддитивном случае и 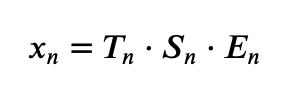
в мультипликативе.
Какова бы ни была цель исследования временных рядов, зачастую рекомендуется с самого начала попытаться разделить и проанализировать каждый компонент. Объясню на нескольких примерах, почему это может быть необходимо.
Зная тенденцию или тенденцию ряда, можно делать прогнозы на несколько пунктов вперед и говорить о характере происходящего процесса в какой-либо долгосрочной перспективе.
Зная характер сезонной составляющей, можно формулировать различные гипотезы, а также корректировать прогноз в зависимости от характера сезонности.
Случайную величину можно изучать, чтобы понять, насколько исследуемый процесс подвержен случайным воздействиям, и попытаться исключить эту случайную часть при построении аппроксимации или прогноза.
Для выделения и анализа каждой части используются специальные статистические приемы и методы.
Анализируя периодограмму ряда, можно установить наличие или отсутствие той или иной компоненты, а также ее характер и относительную величину.
Сама периодограмма является функцией частоты, которая показывает оценку спектральной плотности сигнала.
Давайте посмотрим на это более подробно.
Действительная функция f может быть представлена как сумма синусов и косинусов разных частот с помощью разложения Фурье.
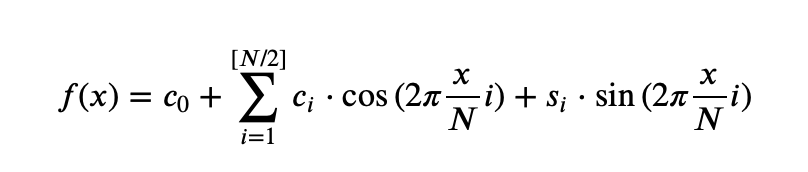
Если вместо функции рассматривать ряд, то сумма квадратов коэффициентов при синусе и косинусе конкретной частоты покажет влияние конкретных частот на значения ряда.
Формально периодограмма записывается следующим образом: 
Перейдем к практике и посмотрим, как все это можно использовать.
Примеры
Рассмотрим примеры для нескольких серий моделей и реальных данных.Сначала рассмотрим простейший ряд, состоящий из нормально распределенной случайной величины с нулевым математическим ожиданием и единичной дисперсией.
Этот ряд называется гауссовским белым шумом.
Давайте сгенерируем тысячу наблюдений гауссовского белого шума.
set.seed(1) par(mfrow=c(2,1)) data <- rnorm(1000, 0, 1) plot.ts(data, type="l") spectrum(data, log='no')

Поскольку определяющих частот для шума вообще нет, то по периодограмме мы видим, что каждая частота входит примерно с одинаковой силой.
По мере увеличения количества наблюдений значение каждой частоты в сетке будет увеличиваться.
Отсюда и название белый шум – все частоты смешаны в равных пропорциях.
Мы не видим идеально равного инвестирования всех частот, поскольку это все же случайная величина, и конкретные отклонения зависят от реализации.
Если при выборе случайного компонента вы получаете что-то подобное, то можете считать, что шум был извлечен правильно.
Отличие красного шума от белого в том, что предыдущие значения влияют на последующие, т.е.
имеют ненулевую корреляцию, в отличие от белого шума.
Мы знаем, как рассчитывается корреляция; соответственно, мы можем выразить красный шум через белый шум с заранее определенным значением корреляции следующим образом: 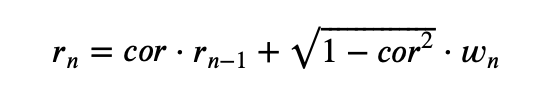
Подробности можно узнать, например, здесь.
set.seed(42)
wnoise <- rnorm(1000, 0, 1)
w0 <- wnoise[1]
wnoise <- wnoise[2:1000]
cor <- 0.8
rnoise = Reduce(function(prev_v, next_v) cor * prev_v + next_v * sqrt(1 - cor^2), wnoise, w0, accumulate = T)
par(mfrow=c(2,1))
plot.ts(rnoise, type="l")
spectrum(rnoise, log='no')
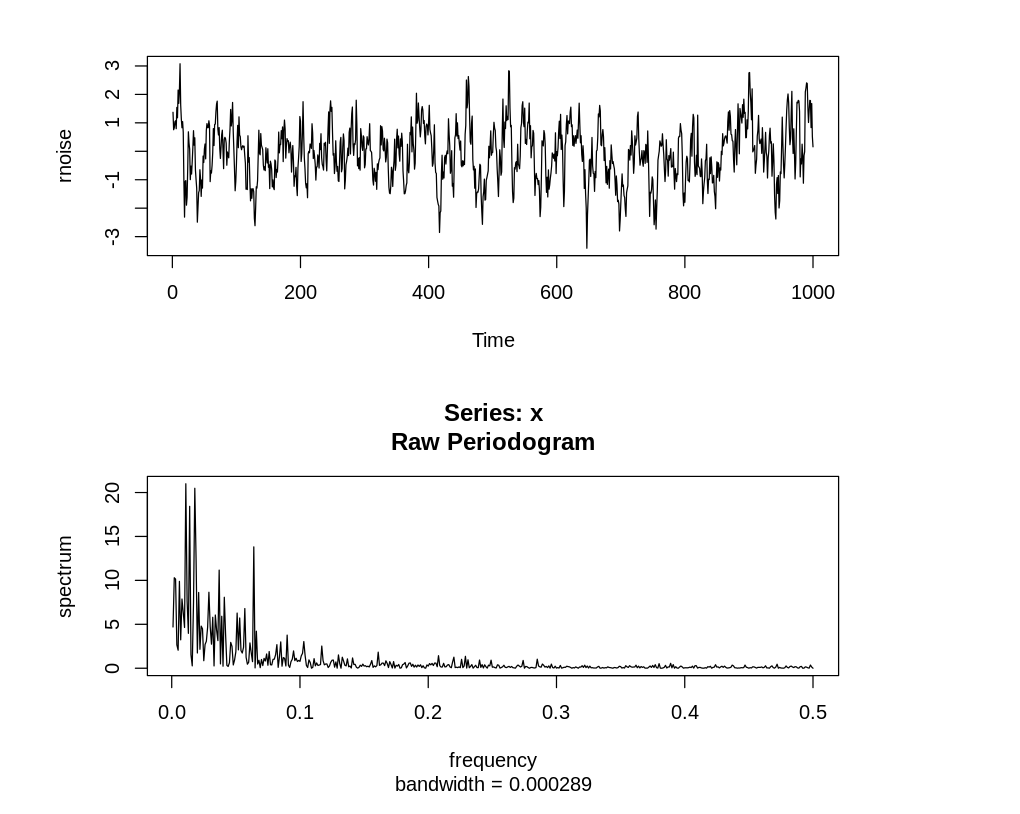
Как и ожидалось, красный шум содержит в основном низкие частоты.
Если мы установим корреляцию ближе к нулю, мы получим белый шум, а если установим ее равным единице, то получим константу, а именно первое значение ряда белого шума.
Теперь предлагаю посмотреть на возможность применения с реальными временными рядами.
Возьмем, к примеру ряд Продажи пива, вина, спиртных напитков исчисляются миллионами долларов.
data <- read.table('.
/shared/MRTSSM4453USN.csv', sep=',', header=T, row.names = 1, )
data <- ts(data, start = c(1992, 1), frequency = 12)
plot(data)

Сезонность, очевидно, есть, посмотрим на периодограмму.
spectrum(data, log='no')
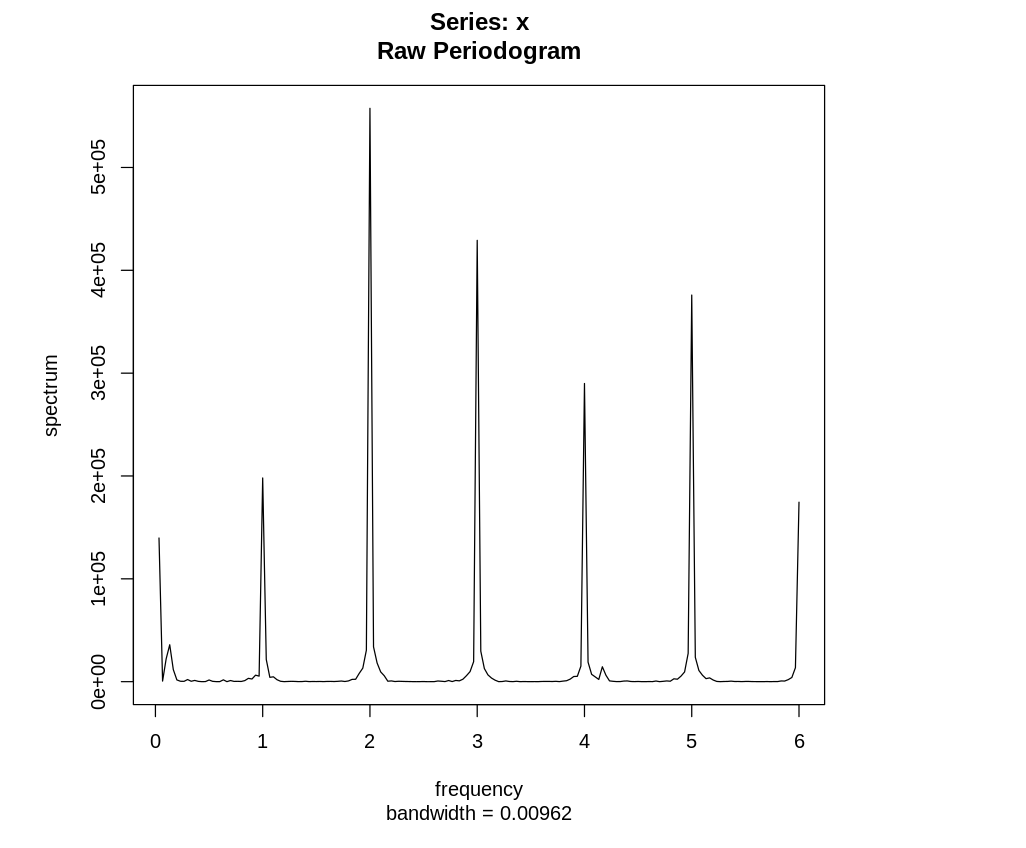
Из графика сразу видно, что наибольшие пики стоимости расположены в сетке сезонности.
Наибольший пик приходится на точку 2, т.е.
в период 2/12, что указывает на наличие полугодовой сезонности.
Остальное можно интерпретировать аналогично.
Мы также видим значения в области низких частот; это медленно меняющаяся составляющая сериала - тенденция.
Таким образом, помимо того, что мы видим, какие частоты преобладают в ряду и какую периодичность имеет ряд, по периодограмме можно также оценить, насколько хорошо мы сгладили ряд. Существует много способов сгладить ряд и выделить тенденцию, и какой из них лучше, нужно решать в зависимости от характера данных.
Для демонстрации мы будем использовать метод классической модели декомпозиции, содержащийся в стандартном пакете статистики языка R. decomposeTs <- stats::decompose(log(data))
plot(decomposeTs)

Давайте посмотрим на периодограмму тренда, сезонности и шума.
spectrum(decomposeTs$trend, log='no', na.action = na.omit)
spectrum(decomposeTs$seasonal, log='no', na.action = na.omit)
spectrum(decomposeTs$random, log='no', na.action = na.omit)
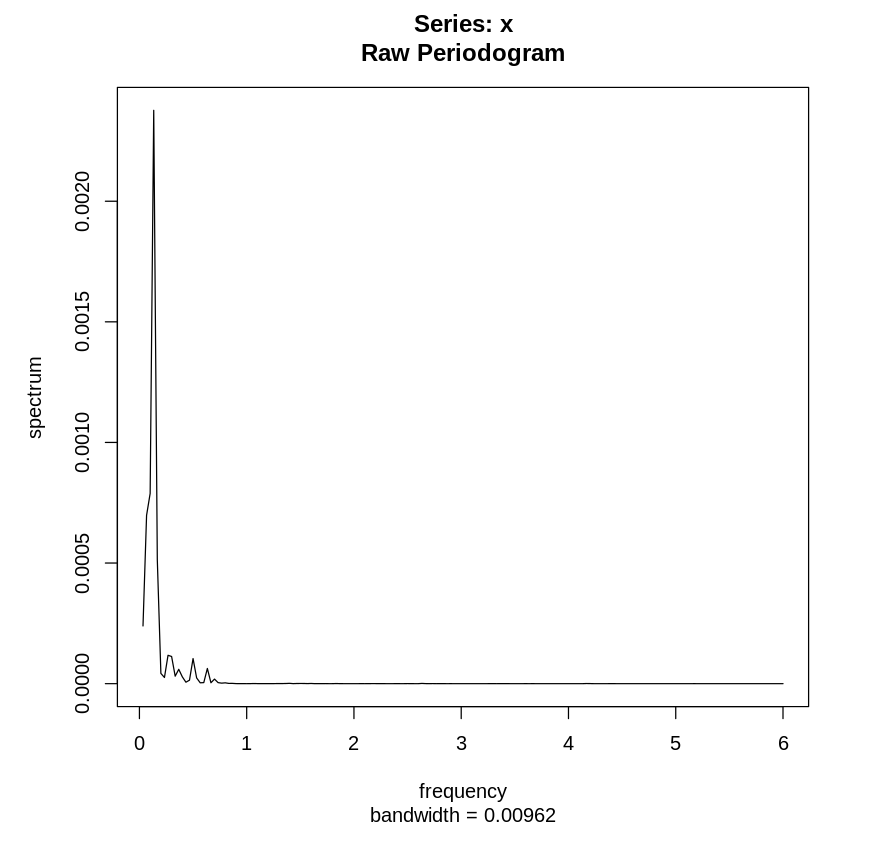

Периодограмма тренда содержит в основном низкие частоты, и это хорошо.
Сезонность слишком идеальна, это связано с методом экстракции, который всегда изолирует чистую сезонность, поскольку оперирует усреднением.
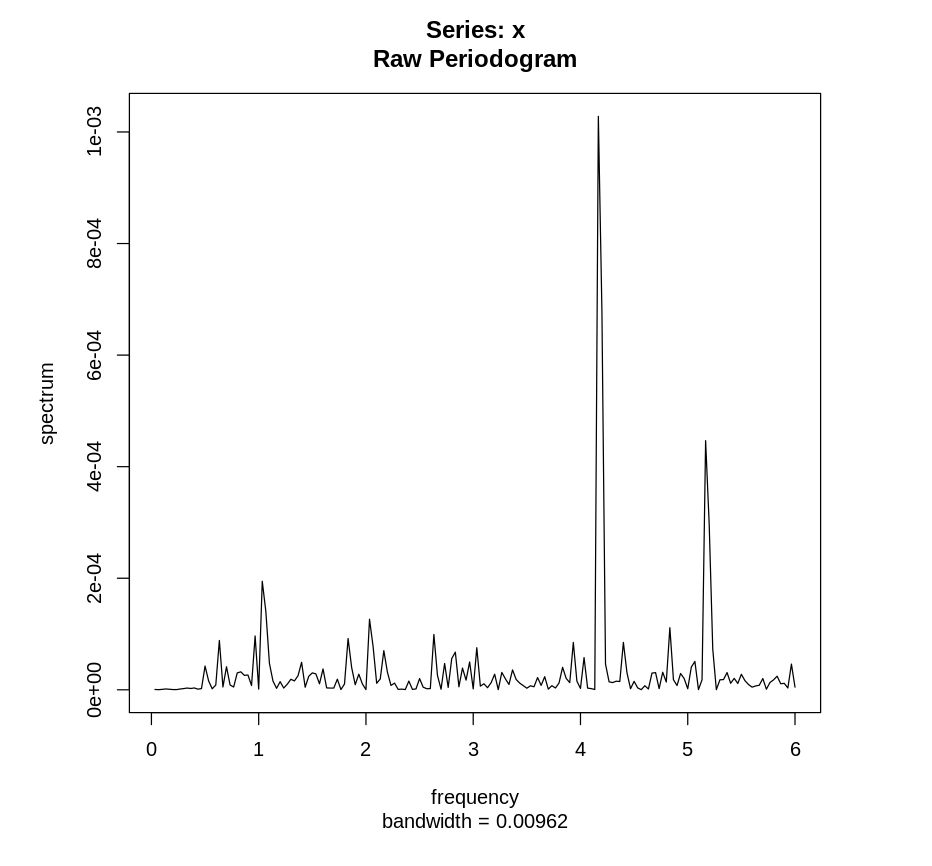
Шум похож на случайную величину, есть пики около 4 и 5, которые обманчиво кажутся большими, но если посмотреть на значение, то можно увидеть, что они не сильно выделяются на фоне шума.
С другой стороны, их можно включить в следующий период сезонности, тогда шум будет еще ближе к случайному.
Для этого примера стоит попробовать другие методы, результаты которых также можно проанализировать с помощью периодограммы.
Теги: #математика #анализ данных #Интеллектуальный анализ данных #временные ряды #r #графики и диаграммы #анализ данных в r
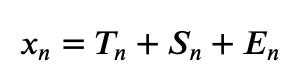
-
Резервное Копирование Вашего Сайта
19 Oct, 24 -
React Против Angular: Что Выбрать
19 Oct, 24 -
Swift И C: Туда И Обратно
19 Oct, 24 -
Яблочный Пирог
19 Oct, 24 -
Мтбанк: По Стопам Мегафона
19 Oct, 24 -
Начались Предзаказы На Apple Watch
19 Oct, 24 -
Машина Тьюринга На Сайте Google
19 Oct, 24


