Добрый день, Хабр Этой статьей я открываю серию статей о том, как обучать нейронные сети без учителя.
(Обучение с подкреплением для нейронных сетей) В серии я планирую сделать три статьи по теории и реализации в коде трех алгоритмов обучения нейронных сетей без преподавателя.
Первая статья будет посвящена градиенту политики, вторая — Q-обучению, третья и последняя статья — методу актера-критика.
Наслаждайся чтением.
Статья первая.
Обучение без учителя с использованием метода градиента политики.
(Градиент политики для обучения с подкреплением)
Введение
Среди алгоритмов машинного обучения особое место занимают алгоритмы машинного обучения, где алгоритм учится решать заданную задачу самостоятельно, без вмешательства человека, напрямую взаимодействуя со средой, в которой он учится.Такие алгоритмы получили общее название – алгоритмы обучения без учителя; для таких алгоритмов нет необходимости собирать базы данных, нет необходимости их классифицировать или размечать.
Алгоритму, который учится без учителя, достаточно давать обратную связь о своих действиях или решениях — хорошие они или нет.
Глава 1: Управляемое обучение
Так что же это такое – Обучение с учителем или без него.Давайте рассмотрим это более подробно на примерах современного машинного обучения и проблем, которые оно решает. Большинство современных алгоритмов машинного обучения для задач классификации, регрессии и сегментации по сути представляют собой алгоритмы обучения с учителем, в которых учителем является сам человек.
Потому что именно человек, размечая данные, сообщает алгоритму, каким должен быть правильный ответ, и тем самым алгоритм пытается найти такое решение, чтобы ответ, который выдает алгоритм при решении задачи, максимально совпадал с ответ, который человек указал для данного задания как правильный ответ. На примере задачи классификации набора данных Mnist правильный ответ, который человек дает алгоритму, — это метка класса цифры в обучающем наборе.

В наборе данных Mnist для каждого изображения, которое машинный алгоритм должен научиться классифицировать, люди предварительно присвоили правильные метки, к какому классу принадлежит это изображение.
В процессе обучения алгоритм, прогнозирующий класс изображения, сравнивает полученный класс для конкретного изображения с истинным классом для того же изображения и постепенно, в процессе обучения, корректирует его параметры так, чтобы класс, предсказанный алгоритмом, стремился к соответствовать классу, указанному человеком.
Таким образом, мы можем обобщить следующую идею: алгоритм обучения с учителем — это любой алгоритм машинного обучения, в котором мы сообщаем алгоритму, что ему нужно делать правильно, с нашей точки зрения.
И не важно, что именно делать — указать, к какому классу отнести это изображение, если это задача классификации, или нарисовать контуры объекта, если это задача сегментации, или в какую сторону повернуть штурвал автомобиль, если алгоритм автопилот, то важно то, что для каждой конкретной ситуации мы четко указываем алгоритму, где правильный ответ и как правильно поступить.
Это ключ к пониманию того, чем алгоритм обучения с учителем принципиально отличается от алгоритма обучения без учителя.
Глава 2. Обучение без учителя
Разобравшись, что это такое – обучение с учителем, давайте теперь разберемся, что это такое – обучение без учителя.Как мы выяснили в прошлой главе, при обучении с учителем для каждой учебной ситуации мы даем алгоритму понимание, какой ответ с нашей точки зрения правильный, затем идем от обратного – при обучении без учителя, для в каждой конкретной ситуации мы не даем такого ответа, алгоритм даст. Но тогда возникает вопрос: если мы не дадим алгоритму явные инструкции, как поступить правильно, то чему же научится алгоритм? Как алгоритм будет учиться, не зная, где подкорректировать свои внутренние параметры, чтобы поступить правильно и в конечном итоге решить задачу так, как хотелось бы.
Давайте подумаем на эту тему.
Нам важно, чтобы алгоритм решал задачу в целом, а вот как именно он будет действовать в процессе решения этой задачи и по какому пути он пойдет, чтобы ее решить, нас это не касается, мы дадим Алгоритм решает сам, мы от него ожидаем только конечного результата.
Поэтому мы дадим алгоритму понять конечный результат, хорошо он решил нашу задачу или нет. Таким образом, также суммируя все вышесказанное, мы приходим к выводу, что алгоритмами неконтролируемого обучения мы называем такие алгоритмы, в которых нет явных указаний алгоритму, что делать, а есть лишь общая оценка всех его действий в процессе решения задачи.
проблема.
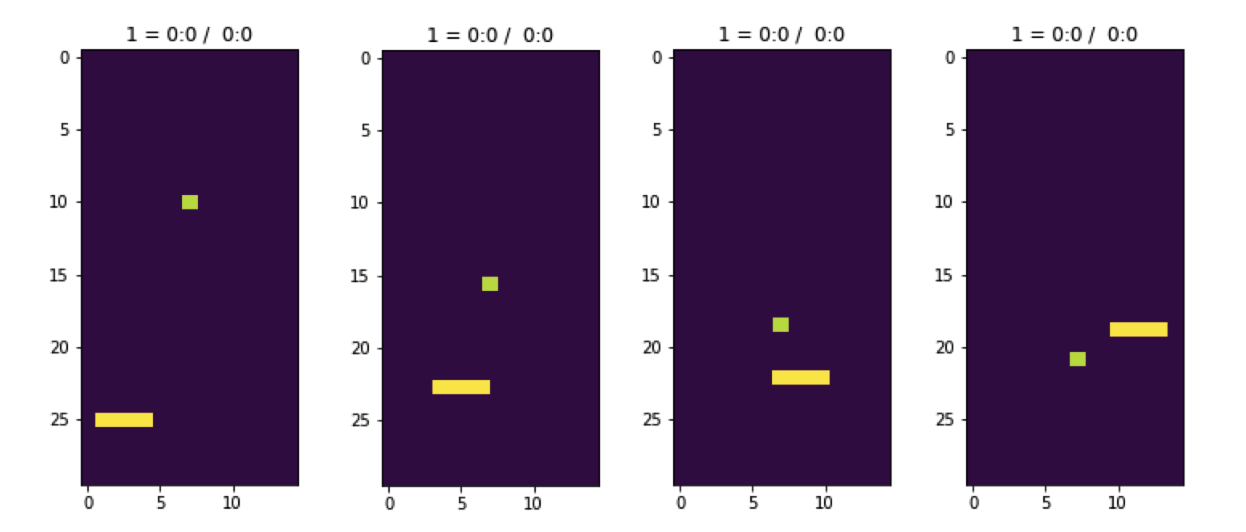
На примере игры, где ракетка пытается поймать падающие сверху кубики, мы не сообщаем алгоритму, управляющему ракеткой, в какой конкретный момент времени куда переместить ракетку.
Алгоритму мы сообщим только результат его действий – поймал он кубик ракеткой или нет.


В этом суть обучения без учителя.
Сам алгоритм должен научиться решать, что делать в каждом конкретном случае на основе итоговой оценки совокупности всех своих действий.
Глава 3. Агент, окружающая среда и вознаграждение
Разобравшись, что такое обучение без учителя, давайте углубимся в алгоритмы, способные научиться решать любую задачу без наших подсказок, как это сделать правильно.Пришло время ввести терминологию, которой мы будем пользоваться в дальнейшем.
Назовем наш алгоритм агентом, который может анализировать состояние среды и совершать в ней какие-то действия.
Окружающая среда — это виртуальный мир, в котором существует наш Агент и своими действиями может менять свое состояние.
Награда — это обратная связь от Среды Агенту как ответ на его действия.
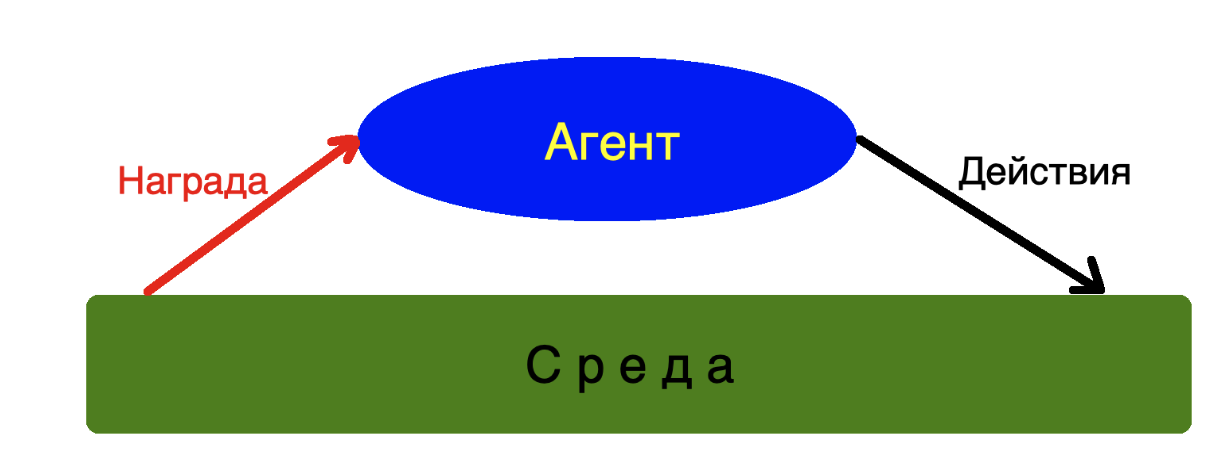
Среда, в которой живет наш агент, может быть сколь угодно сложной; агент может даже не знать, как он работает, чтобы принимать решения и выполнять действия.
Для Агента важна только обратная связь в виде вознаграждения, которое он получает от окружения.
Если рассмотреть более подробно процесс взаимодействия агента и среды, то его можно выразить следующей схемой 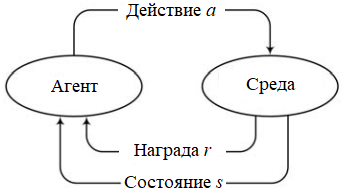
St — состояние среды (state) на шаге t
at — действие агента (действие) на шаге t
rt — награда на шаге t
В каждый момент времени t наш агент наблюдает за состоянием среды - St, совершает действие - at, за что получает вознаграждение от среды - rt, поле которого среда переходит в состояние St+1, что наш агент наблюдает, выполняет действие - at+1, за это получает награду от среды - rt+1 и таких состояний у нас может быть бесконечное количество t - n.
Глава 4. Параметризация задачи неконтролируемого обучения
Чтобы обучить агента, нам нужно как-то параметризовать задачу неконтролируемого обучения, то есть понять, какие именно функции мы собираемся оптимизировать.В обучении с подкреплением — в дальнейшем мы будем называть обучение без учителя — есть три основные функции: 1) p(a|s) — функция политики Вероятностная функция оптимальности действия – это зависимость от состояния среды –s. Оно показывает нам, насколько оптимально действие a в состоянии окружающей среды s. 2) v(s) - функция значения Функция значения состояния — s. Это показывает нам, насколько ценно для нас состояние в целом с точки зрения вознаграждения.
3) Q(s,a) — Q-функция Q-функция оптимальной стратегии.
Оно позволяет нам по заданной оптимальной стратегии выбрать оптимальное действие для данного состояния – Во-первых, давайте рассмотрим функцию — функцию политики, как самую простую и интуитивно понятную функцию обучения с подкреплением.
Потому что мы собираемся решать задачи обучения с подкреплением с помощью нейронных сетей.
Тогда схематически мы можем параметризовать функцию политики через нейронную сеть следующим образом.
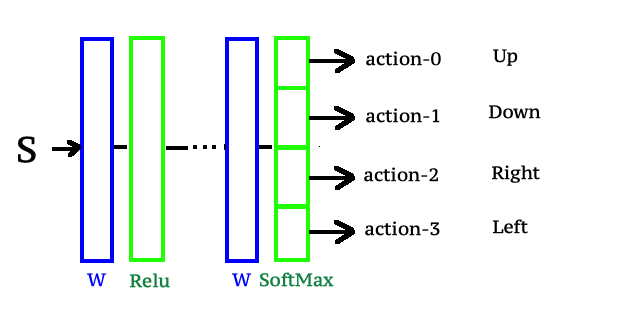
Мы будем подавать состояния - s - на вход нейронной сети, а выход нейронной сети спроектируем таким образом, чтобы выходной слой нейронной сети представлял собой слой SoftMax с количеством выходов, равным количество действий, возможных для агента в нашей среде.
Таким образом, пропуская выходное состояние s через слои нейронной сети, мы получаем распределение вероятностей действий агента в состоянии s. Что нам действительно нужно, так это начать обучение нашей нейронной сети с помощью алгоритма обратного распространения ошибки и итеративно улучшать функцию политики, которая теперь по сути является нашей нейронной сетью.
Глава 5. Улучшение функции политики посредством обучения нейронных сетей
Для обучения нейронной сети мы используем метод градиентного спуска.
Поскольку последним слоем нашей нейронной сети является слой SoftMax, его функция потерь равна: 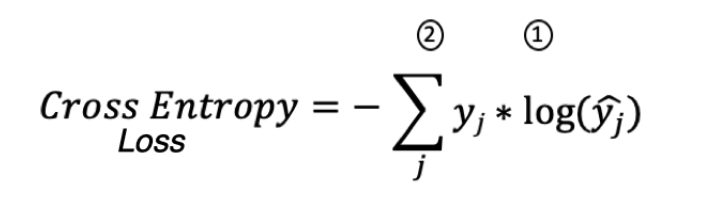
Где:
1 — истинные метки * журнал (прогнозируемые метки)
2 - сумма для всех примеров
Однако как мы можем обучать нейронную сеть, если у нас еще нет правильных меток для действий агента в состояниях S0-Sj? Но они нам не нужны; вместо правильных меток мы будем использовать вознаграждение, которое агент получил от среды после выполнения действия, которое ему предсказала нейросеть.
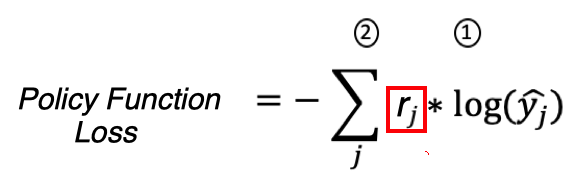
Мы имеем на это полное право, потому что для Cross Entropy Loss — yj — это истинные метки правильного класса и они равны единице, а для Policy Function Loss — rj — вознаграждение, которое среда присуждает агенту за действие, которое он совершил.
То есть rj служит весом для градиентов во время обратного распространения ошибки, когда мы обучаем нейронную сеть.
Если получено положительное вознаграждение, значит, нужно увеличить веса нейронной сети, куда направлен градиент. 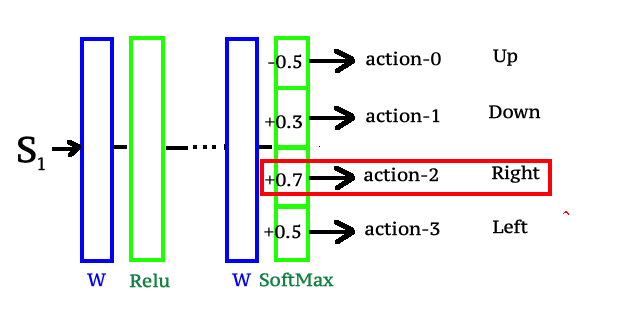
Если полученное вознаграждение отрицательное, то соответствующие веса в нейронной сети уменьшаются в соответствии с направлением градиента, в котором направлена ошибка.
Глава 6. Сборка DataSet для обучения
Чтобы обучить нашего Агента — нейронную сеть с использованием классического машинного обучения — методом обратного распространения ошибки, нам необходимо собрать набор данных.
Из постановки задачи понятно, что мы хотим на вход нейросети подать состояние среды S — изображение колодца с падающими кубиками и ракеткой, которая их ловит. 
a Y – который мы будем собирать в соответствии с состоянием S, это и будет прогнозируемое действие нейронной сети – a и вознаграждение, которое среда наградила агента за это действие – r 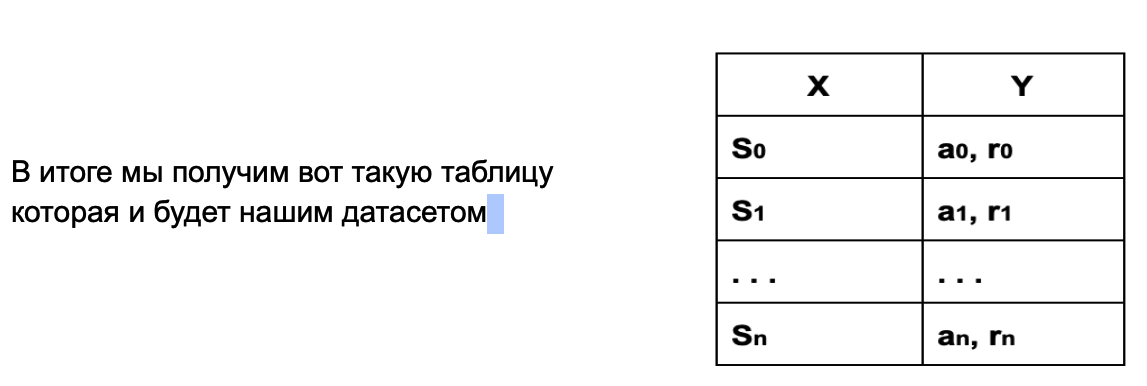
Но во время игры среда может не назначать агенту вознаграждение за каждое действие; например, в нашем случае агент получит положительное вознаграждение только тогда, когда ракетка поймает падающий кубик.
Если ракетка не поймает кубик и он упадет на дно, то среда назначит агенту отрицательное вознаграждение.
В остальное время, независимо от того, как агент двигает ракетку, пока кубик либо не ударится о ракетку, либо не упадет на дно, среда будет давать агенту вознаграждение, равное нулю.

Как видно из описания процесса нашей игры, положительное или отрицательное вознаграждение для агента возникает крайне редко, и вообще вознаграждение, независимо от его действий, равно нулю.
Как обучить Code Agent большую часть времени он не получает ответа от среды на свои действия.
С точки зрения того, что наш агент — нейросеть и вознаграждение от среды равно нулю, то градиенты при обратном распространении ошибки через нейросеть в большинстве случаев в наборе данных будут равны нулю, веса нейронной сети некуда будет меняться, а значит наш агент ничему не научится.
Как решить проблему с нулевым вознаграждением в большей части набора данных, собираемого для обучения агентов? Есть два пути выхода из этой ситуации: Первый — назначить всем действиям агента, которые он совершил за время падения кубика, одну и ту же итоговую награду за эпизод +1 или -1, в зависимости от того, поймал ли агент кубик или не поймал.
Таким образом, мы будем считать все действия Агента, если он поймал кубик, правильными и будем подкреплять такое поведение агента во время обучения, назначая ему положительное вознаграждение.
Если Агент не поймал кубик, то мы назначим отрицательное вознаграждение всем действиям Агента в эпизоде и обучим его избегать такой последовательности действий в дальнейшем.
второй — распространить итоговое вознаграждение с определенным шагом нисходящей скидки на все действия агента в этом эпизоде.
Другими словами, чем ближе к завершению действие агента, тем ближе награда за это действие к +1 или -1. Вводя такое дисконтированное вознаграждение за действие, уменьшающееся по мере удаления действия от конца эпизода, мы даем понять Агенту, что последние действия, которые он совершил, более важны для исхода эпизода Игры, чем действия, которые он совершил в начало.
Обычно дисконтированное вознаграждение рассчитывается по формуле - Итоговое вознаграждение эпизода умножается на коэффициент дисконтирования в степени номера шага минус единица за все действия агента в эпизоде (за время, пока выпала игральная кость).
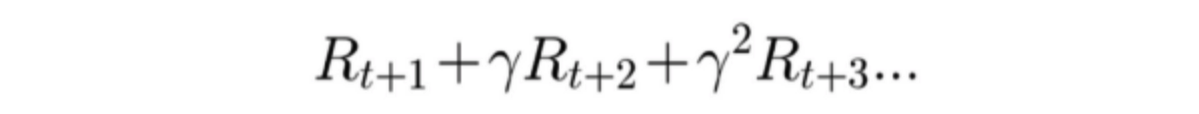
Гамма – коэффициент дисконтирования (уменьшения вознаграждения).
Оно всегда находится в диапазоне от 0 до 1. Обычно гамма принимается в районе 0,95. После того, как мы определились, какие данные будем собирать в DataSet, запускаем симулятор среды и, играя несколько раз подряд в игру с несколькими эпизодами, собираем данные о:
- состояние окружающей среды,
- действия, предпринятые Агентом,
- награда, которую получил Агент.
Это значит, что в одной игре мы по очереди будем бросать в колодец несколько кубиков, а ракетка будет пытаться их поймать.
За каждый пойманный кубик агенту начисляется +1 очко, за каждый кубик, упавший на дно и ракетка его не поймала, агенту начисляется -1 очко.
Глава 7. Внутренняя структура агента и среды
Окружение — так как наша среда, в которой будет существовать агент, по сути является матрицей колодца, внутри которого со скоростью одна строка за такт кубы падают вниз, а агент ходит в одном направлении, тоже на одну ячейку.Мы напишем симулятор среды, который сможет сбросить кубик с верхней строки в произвольном столбце в случайный момент времени, сможет по получении команды от агента переместить ракетку на один квадрат в одном из направлений, а затем проверить был ли падающий кубик пойман ракеткой или, может быть, он упал на дно колодца.
В зависимости от этого симулятор возвращает агенту вознаграждение, которое он получил за свое действие.
Агент — основной элемент которого — наша нейронная сеть, способная возвращать вероятности всех действий для заданного состояния среды на основе состояния среды, данного ему на входе.
Из вероятности действий, полученных от нейронной сети, агент выбирает лучшее, отправляет его в среду и получает от среды обратную связь в виде вознаграждения от среды.
Агент также должен иметь внутренний алгоритм, на основе которого он сможет научиться максимизировать вознаграждение, полученное от среды.
Глава 8. Обучение агентов
Для обучения Агента нам необходимо накапливать статистику на основе данных нашего симулятора и действий, совершаемых агентом.Статистические данные для обучения будем собирать по тройкам значений — состояние среды, действие агента и вознаграждение за это действие.

Небольшой код о том, как собирать статистику

Каждую такую тройку значений мы помещаем в специальный буфер памяти, где храним их все время, пока моделируем игру и накапливаем по ней статистику.
Код для организации буфера памяти:
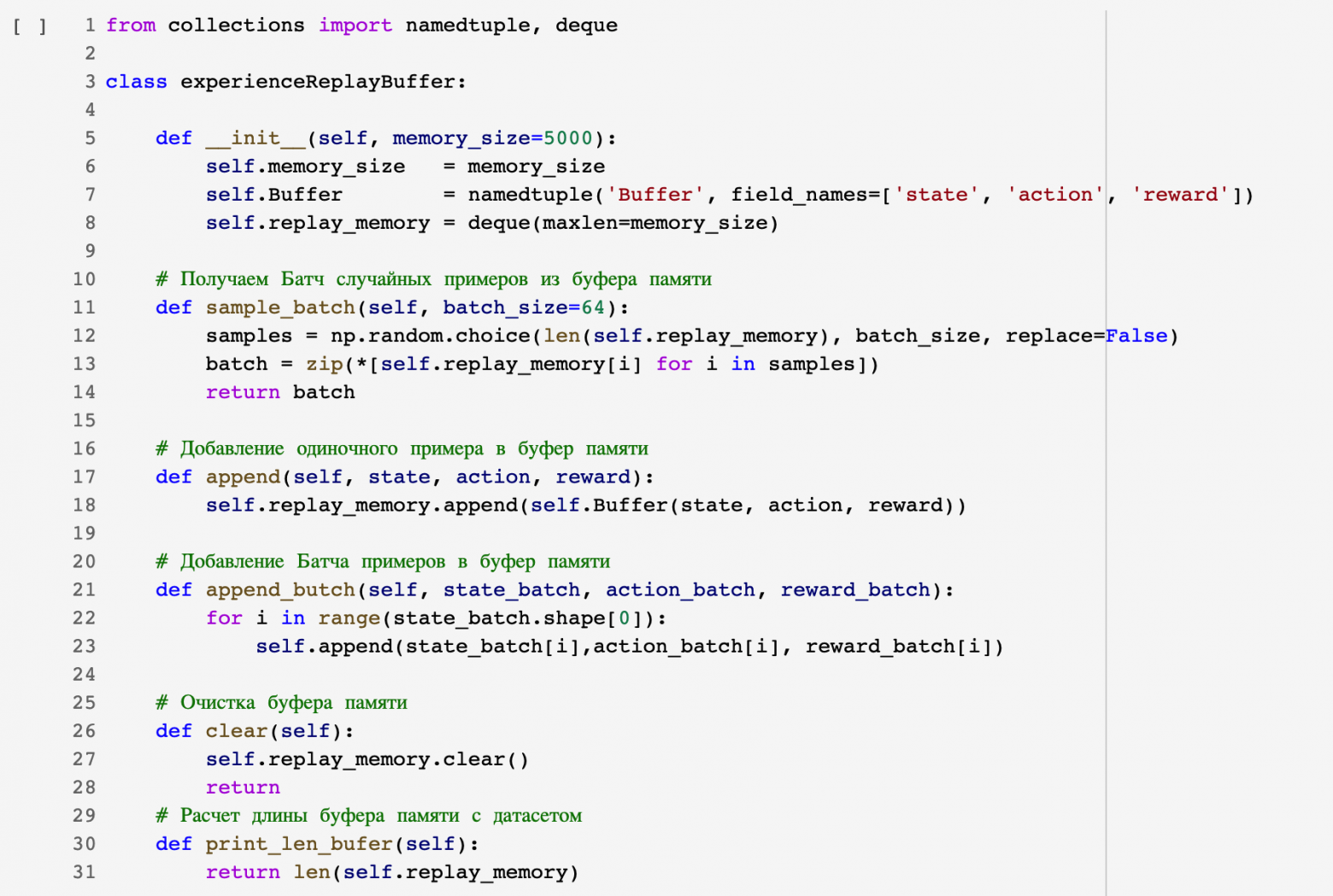
Сыграв серию игр между нашим Агентом и Средой и накопив статистику, мы можем перейти к обучению Агента.
Для этого мы получаем пакет наших данных в виде троек значений из буфера памяти с накопленной статистикой, распаковываем его и конвертируем в тензоры Pytorch. 
Мы подаем набор состояний окружающей среды в форме тензора Пайторха в качестве входных данных в нейронную сеть агента, получаем распределение вероятностей для каждого движения агента для каждого состояния среды в совпадении, берем логарифм этих вероятностей, умножаем на вознаграждение, полученное агентом за ход, логарифмом этих вероятностей, затем берем среднее значение произведений и делаем это среднее отрицательным: 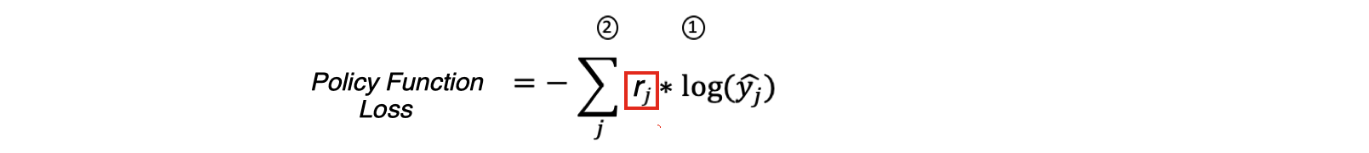
Энажмите 1 
Энажмите 2 
После того, как мы получили значение функции Loss, мы делаем обратный проход по нейронной сети, чтобы получить градиенты, и делаем шаг с оптимизатором для корректировки весов.
На этом цикл обучения нашего агента завершается.
Так как после того, как оптимизатор сместил веса нейросети, наши данные, собранные в статистике, уже не актуальны, потому что нейросеть со сдвинутыми весами будет выдавать совершенно разные вероятности действий на одних и тех же состояниях среды и обучение агента продолжится.
пойти не так.
Поэтому мы очищаем наш буфер памяти, снова играем определенное количество игр для сбора статистики и перезапускаем процесс обучения агента.
Это цикл обучения без учителя с использованием метода Policy Gradient.
- Накопление статистических данных
- Обучение агентов
- Сброс статистики
Глава 9. Эксперименты с агентом и средой
Запустим серию экспериментов по обучению нашего Агента.
Для экспериментов выберем следующие параметры окружающей среды: 
Для Агента выберем - построим нейронную сеть - она будет сверточной (так как мы работаем с изображением) на выходе у нее будет 9 выходов (1-правый, 2-левый, 3-вверх, 4- вниз, 5-вправо вверх, 6-влево-вверх, 7-вправо-вниз, 8-влево-вниз, 9-ничего не делать) и SoftMax для получения вероятности каждого действия.
Архитектура нейронной сети
Размер изображения 32 нейронов первого слоя Conv2d 1*32*16 Размер изображения слоя MaxPool2d 32*16*8 Размер изображения 32 нейронов второго слоя Conv2d 32*16*8 Размер изображения слоя MaxPool2d 32*8*4 Flatten — выпрямить изображение до размера 1024. Линейный слой с 1024 нейронами Слой выпадения (0,25) Линейный слой с 512 нейронами Линейный слой с 256 нейронами Линейный слой с 9 нейронами и SoftMax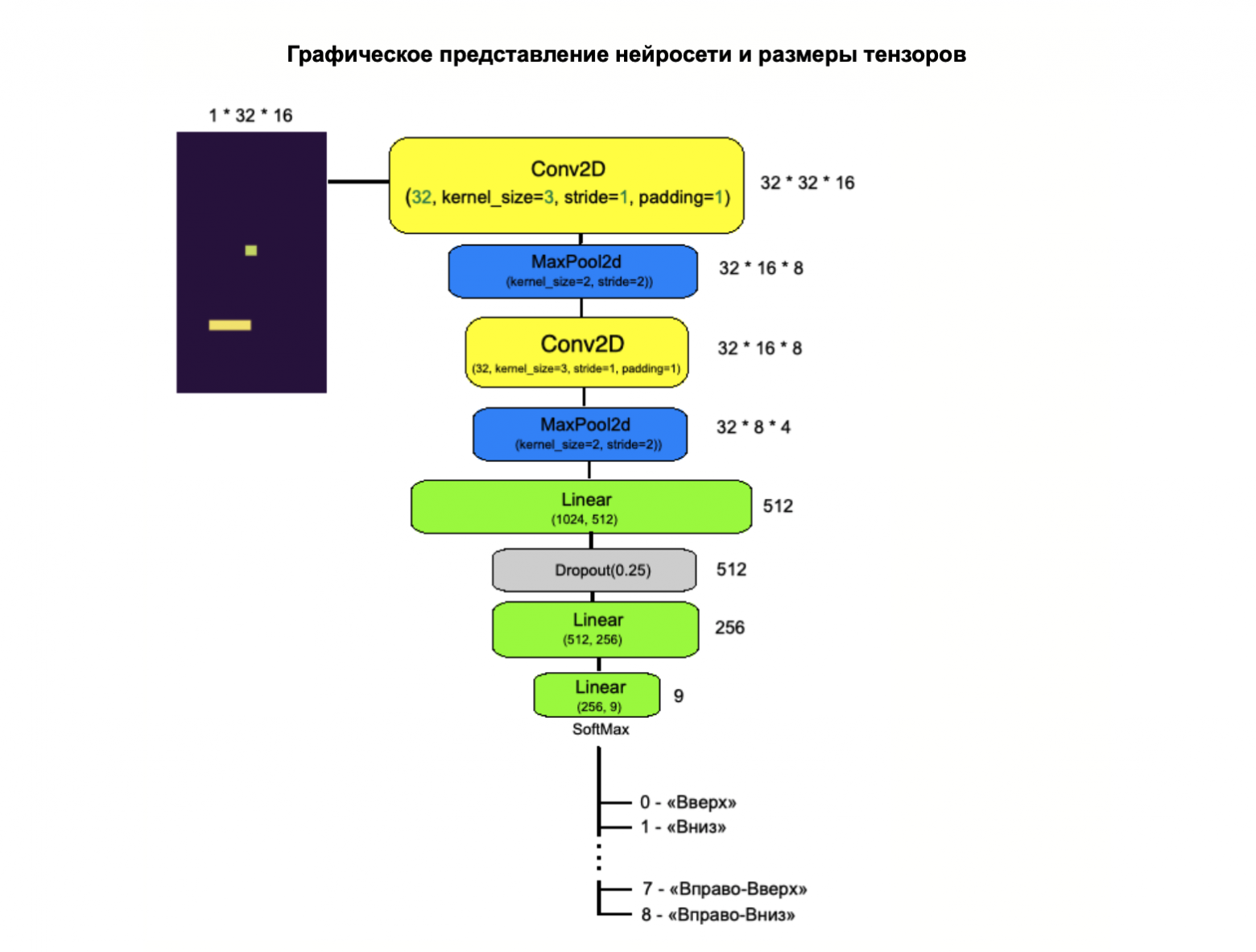
Код для создания нейронной сети в Pytorch

Мы поочередно запустим три цикла обучения Агента в Среде, параметры которых были рассмотрены выше:
Ээксперимент №1 - Агент научился решать задачу за 13600 игровых циклов
Исходное состояние агента
График обучения агентов
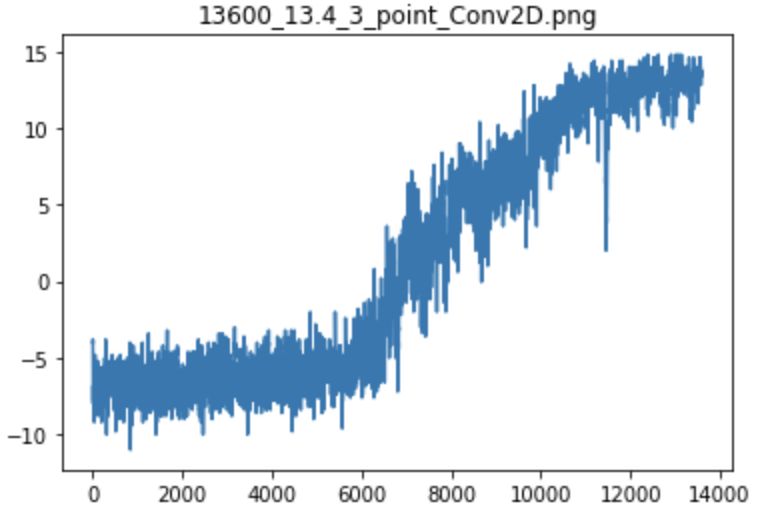
Состояние обучения агента

Ээксперимент №2 - Агент научился решать задачу за 8250 игровых циклов
Исходное состояние агента
График обучения агентов
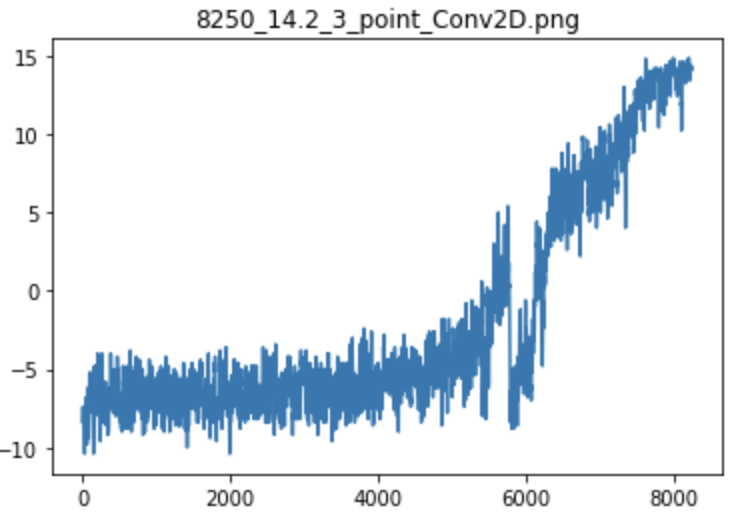
Состояние обучения агента

Ээксперимент №3 - Агент научился решать задачу за 19800 игровых циклов
Исходное состояние агента
График обучения агентов
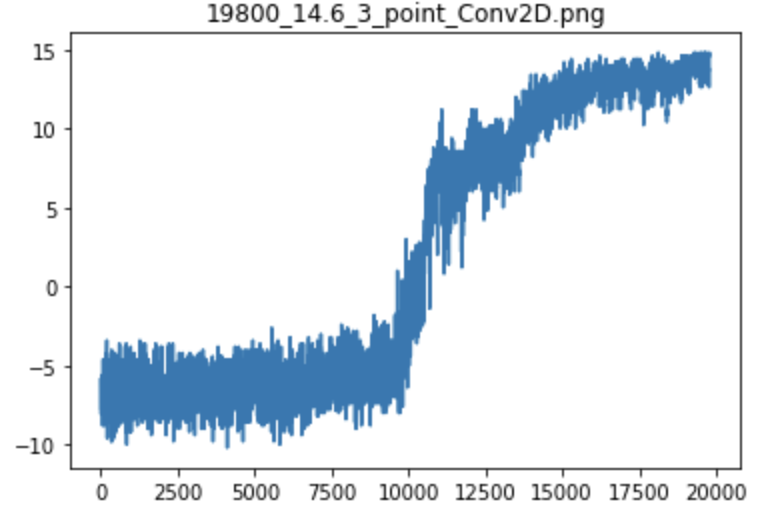
Состояние обучения агента

Глава 10. Выводы
Глядя на графики, можно сказать, что обучение Агента, безусловно, идет медленно.Агент изначально тратит довольно долгое время на поиск хоть какой-то разумной политики своих действий, чтобы начать получать положительное вознаграждение.
В это время на первом этапе графика происходит медленный рост вознаграждения за игру, затем вдруг Агент находит хороший вариант своих ходов, и полученное им вознаграждение за игру резко увеличивается вверх и продолжается дальше.
подъем, а затем, приближаясь к максимальному вознаграждению, агент снова имеет медленный рост эффективности, когда он совершенствует уже изученную им политику ходов, но стремится, как и любой жадный алгоритм, забрать вознаграждение себе полностью.
Также хотелось бы отметить большую необходимость вычислений для обучения Агента методом Policy Gradient, т.к.
большую часть времени алгоритм работает именно на сборе статистики ходов Агента, а не на его обучении.
Собрав статистику ходов со всего массива, мы используем только один пакет данных для обучения Агента, а все остальные данные отбрасываем как непригодные для обучения.
И снова мы собираем новые данные.
С этим алгоритмом и средой можно экспериментировать еще очень много — меняя глубину и ширину колодца, увеличивая или уменьшая количество выпадающих кубиков за игру, делая эти кубики разных цветов.
Понаблюдать, какое влияние это окажет на эффективность и скорость обучения Агента.
Здесь тоже огромное поле для экспериментов — параметры нейросети, собственно нашего Агента, которого мы обучаем; вы можете менять слои, ядра свертки, включать и настраивать регуляризацию.
И многое другое можно попробовать, чтобы повысить эффективность обучения агентов.
Таким образом, запустив практические эксперименты с неконтролируемым обучением с использованием метода Policy Gradient, мы убедились, что неконтролируемое обучение имеет место и оно действительно работает. Агент самостоятельно научился максимизировать свое вознаграждение в игре.
Ссылка на GitHub с кодом, адаптированным для работы на ноутбуке Google Colab. Теги: #Машинное обучение #python #Алгоритмы #искусственный интеллект #нейронные сети #обучение с подкреплением #обучение без учителя

-
Библиотека Сериализации Json Для Erlang
19 Oct, 24 -
Кто Изобрел Двойную Бухгалтерию?
19 Oct, 24 -
Сергей Брин По Русски
19 Oct, 24


