Часть 1. Введение Часть 2: Балансировка и установка Я довольно долго боролся с красно-черным деревом( дальше - кчд ).
Вся информация, которую я нашел, была в духе «листья и корень дерева всегда черные ПОТОМУ ЧТО», «топ-5 свойств красно-черного дерева» или «3 случая при балансировке и 12 случаев при удалении узла».
Меня такая расстановка не устраивала.
Я не хотел запоминать свойства дерева, псевдокод и параметры балансировки, я хотел знать, почему.
Как цвета помогают сбалансироваться? Почему у красного узла не может быть красного дочернего узла? Почему глубину дерева измеряют «черной высотой»? Ответы на эти вопросы я получил только тогда, когда мне дали ссылку на лекцию о два-три дерева, с чего мы и начнем.
Данная статья разделена на 3 логические части.
Рекомендую читать их в указанном порядке.
Первая часть (эта) будет направлена на знакомство и знакомство с CCD. Во второй части поговорим о балансировке и прошивке в cchd. В третьей и заключительной части мы разберем процесс удаления узла.
Наберитесь терпения и наслаждайтесь чтением :) Отказ от ответственности
- В этой статье не будет информации о плюсах и минусах дерева, его применении и т. д.: информации об асимптотике дерева и работе с ним в Интернете достаточно.
- Материал предназначен для тех, кто уже знаком с ПЗС и теперь хочет в них разобраться, а также для тех, кто только знакомится с ними.
- В статье не будет подробностей реализации конструкции.
- Можно предположить, что данная статья представляет собой перевод англоязычного видеоматериала в упрощенную русскую текстовую версию.
Все ссылки оставляю в конце статьи.
Два-три дерева
Чтобы понять красно-черное дерево, нужно понять дерево два-три.Забегая вперед, скажу, что два-три дерева – это, по сути, родитель наш cchd, поэтому важно начать с него.
Если мы поймем два или три дерева, мы поймем КЧД.
Два-три дерева - абстрактный тип данных , по структуре напоминающий дерево.
В узлах двух или трех деревьев может быть одно или два значения и два или три дочерних элемента.
(ниже узнаем, от чего зависит количество значений и потомков узла).
Мы вызовем узел с одним значением и двумя дочерними элементами.
2-узловой , узел с двумя значениями и тремя детьми — 3-узловой .
Я начну свое объяснение с создания такого дерева: оно понятно и просто.
Но в начале все же необходимы некоторые пояснения:
- Когда мы добавляем элемент, мы всегда перемещаемся вниз по дереву.
- Дерево сортируется классически — меньшие значения находятся слева, большие — справа.
- Дерево «два-три» — отсортированное, сбалансированное дерево.

Добавим число 12. К корню тоже добавим число 12 (помним, что узел может иметь два значения), но теперь нам нужно «отсортировать» наш узел (сортировать два элемента, ха), т.е.
расположить их по возрастанию .
Результатом является узел 5-12. 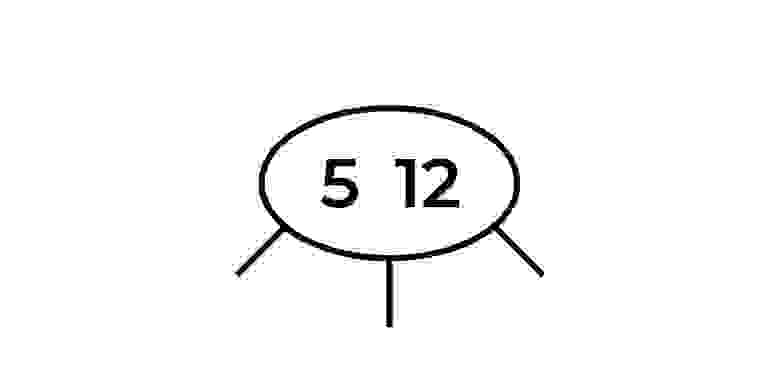
Добавим следующее число.
Пусть это будет 17. Давайте пока добавим наш элемент в один узел и отсортируем его еще раз.
Результатом стал узел 5-12-17. Внимательный читатель заметит здесь подвох — выше я говорил, что наши узлы могут содержать не более двух элементов.
Вот где происходит волшебство! Берем средний элемент нашего узла и «струйкой» его наверх.
Результат виден на картинке.
Корнем было число 12, левым сыном было число 5, а правым сыном было 17. 
То, что мы сделали выше, можно назвать балансировка двух или трех деревьев .
Правило этого балансирования простое: если в узле три значения, «сливаем» среднее значение вверх .
Алгоритм действий зависит от 3-х условий:
- Узел является корнем.
Тогда ничего не остается, как создать новый узел с одним значением и сделать его новым корнем (как в нашем случае).
- Родительский узел имеет одно значение.
Затем мы просто добавляем значение к родительскому элементу и завершаем балансировку (при этом у родительского элемента появляется третий дочерний элемент).
- Родительский узел имеет два значения.
Затем мы снова увеличиваем значение, пока не дойдем до первой или второй точки.
Хорошо, давайте двигаться дальше.
Добавим цифру 3. Поскольку теперь мы не ограничены одним узлом, спускаемся вниз.
Понятно, что вам нужно спуститься влево и добавить 3 к узлу со значением 5. Не забудьте расставить 3 и 5 в правильном порядке.
Результатом стал узел 3-5. 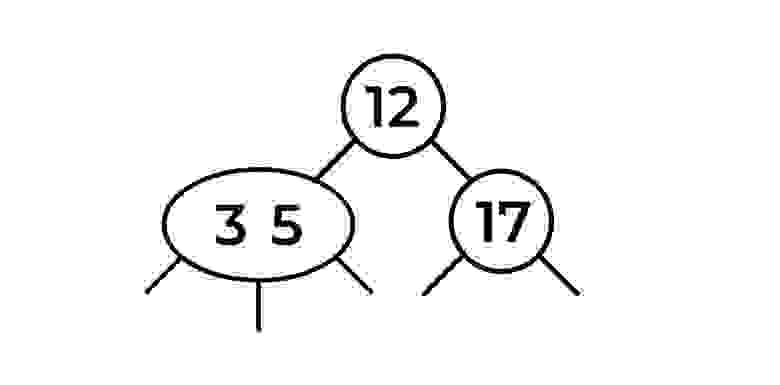
Наберитесь терпения, мы приближаемся к самому интересному :) Давайте добавим цифру 4, которая также пойдет влево и присоединится к узлу 3-5. В результате получается узел 3-4-5, который, как мы уже знаем, необходимо привести к нужной форме.
Что мы делаем? Балансируем наше дерево, т.е.
«сливаем» значение 4 наверх.
Теперь самое интересное.
Помимо того, что мы добавим к корню 4, мы также добавим к корню третьего дочернего элемента — это будет тот узел, который был больше 4. В нашем случае это 5. Картина будет выглядеть так: 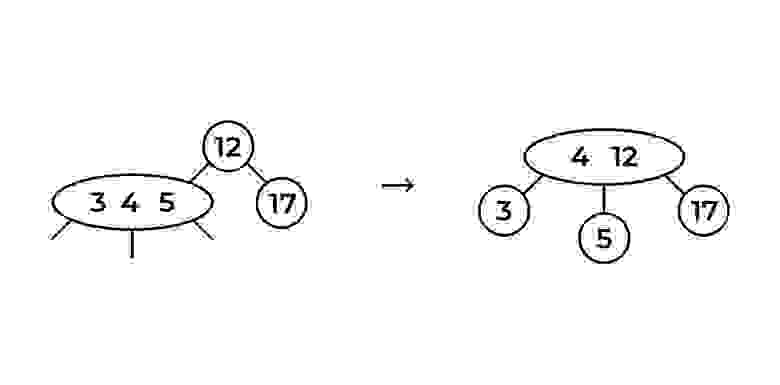
Почему 5 не могла оставаться в своем узле? Здесь мы вспоминаем правило отсортированного дерева: меньшие значения находятся слева, большие значения — справа.
А поскольку 5 больше 4, мы не можем оставить 5 слева, потому что это нарушит наш инвариант. Поэтому узлу со значением 5 ничего не остается, как «переместиться» и стать дочерним элементом узла 4-12 (кстати, если бы у 5 были дочерние элементы, они бы тоже «переехали» вместе с родителем).
Здесь нам нужно сделать небольшую паузу и объяснить, как перемещаться по узлам с тремя детьми.
Это просто:
- Значение, меньшее левого значения в узле, будет левым дочерним элементом.
- Значение, которое больше левого, но меньше правого значения в узле, будет средним дочерним элементом.
- Значение, которое больше правильного значения в узле, будет правильным дочерним элементом.

Теперь посмотрите, что произошло.
Мы можем смело сказать, что это сортированное, сбалансированное два-три дерева.
Меньшие значения лежат слева, большие — справа (здесь, как и в случае со значениями 4-5-12, мы считаем, что 5 лежит правее 4 и левее 12).
Корень имеет два значения и три дочерних элемента, что абсолютно соответствует описанию дерева выше.
Теперь вы можете попробовать добавить любое значение самостоятельно, чтобы убедиться, что понимаете логику (что произойдет с деревом, если вы добавите значение 7? А потом 9?).
Ладно, надеюсь, с самим деревом мы разобрались.
Ноды добавлены, дерево сбалансировано, можно искать, все отлично.
Но есть нюансы.
Главный недостаток такой структуры в том, что, в отличие от бинарного дерева, ее неудобно реализовывать.
Нужно следить за количеством потомков и их ценностью, плюс их порядок и балансировку (а об удалении я еще не говорил).
Красно-черное дерево решает эту проблему.
Красно-черное дерево
Как мы выяснили, основным недостатком двух-трех деревьев является их строение.Тогда давайте попробуем превратить дерево два-три в бинарное дерево.
Как мы можем это сделать? Чтобы добиться этого, нам нужно простое трехузловое представление.
Разделим 3-узла на два 2-узла и соединим их ссылками.
Пометим эти ссылки каким-нибудь свойством, например, цветом (возьмем красный), чтобы отличать такие ссылки в дереве от всех остальных.

Вообще говоря, мы не можем пометить сами ссылки, поэтому мы помечаем узлы.
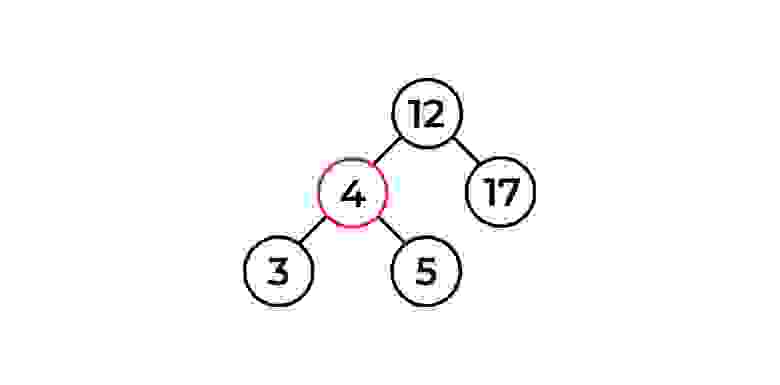
Итак, вот красно-черное дерево.
Далее мы рассмотрим несколько свойств cfd, которые я считаю важными (но думаю, что многое уже стало понятно из прочтенного выше).
Свойства красно-черной древесины
Спойлер На самом деле мы анализируем не просто ПЗС, а левосторонний КЧД — одна из реализаций КЧД, в которой могут располагаться красные узлы только левый , то есть от 3-узла мы всегда будем отделять значение меньше (что и было сделано выше).По сути, левая ПЗС ничем не отличается от обычной, разве что является более простой и понятной реализацией.
Подобно левостороннему CCHD, существует также правостороннее движение улитки (логику додумайте сами).
Свойство 1. Два красных узла не могут находиться подряд. Это свойство имеет смысл, если мы знаем, что красный узел по существу является частью 3-узла в дереве 2-3. Ну а если два красных узла идут подряд, то получается 4-узловой, которого у нас нет :) Свойство 2. Корень дерева всегда черный.
Опять же, здесь все ясно: красный узел не может существовать без родителя.
Свойство 3. Все нулевые узлы (узлы, у которых нет дочерних элементов) черные.
Я не нашел объяснения, почему это так.
Но позвольте мне сказать, что это довольно удобное правило, когда дело касается балансировки дерева.
О потомках Раз уж мы затронули нулевые узлы, то стоит сказать, что все узлы в дереве всегда должны иметь двух дочерних узлов, и если ссылка на дочерний элемент равна нулю, то она ведет непосредственно к нулевому узлу.
Фактически, это поднимает вопрос реализации; мне было удобнее добавить нулевой узел (меньше проблем с итераторами, балансировкой и т.п.
).
Свойство 4. Высота дерева измеряется только черными узлами и называется «черной высотой».
Здесь опять же все в целом становится очевидным: красный узел — это лишь дополнение к черному узлу, он является его частью, поэтому высоту обычно рассчитывают исходя из черных узлов.
На этом введение заканчивается.
В следующая часть мы поговорим о том, как вставлять узлы в дерево и сбалансировать его.
Теги: #C++ #структуры данных #бинарные деревья

-
Заглянем В Будущее Ит На 500 Лет
19 Oct, 24 -
Умный Дом. Начинать
19 Oct, 24 -
Firefox Rc3 Доступен Пользователям
19 Oct, 24 -
Поиск По Скриншотам Сайта
19 Oct, 24 -
Хакатон И Геймджем В Екатеринбурге
19 Oct, 24


