В современном мире сложно представить разработку продукта без A/B-тестирования.
Для успешного запуска продукта или нового функционала необходимо грамотно спроектировать A/B, просчитать и интерпретировать его результаты.
Иногда нам необходимо тестирование более чем двух групп.
В этой статье мы рассмотрим именно такой случай — множественное тестирование:
- Давайте поговорим о том, когда и почему следует проводить несколько тестов;
- Давайте рассмотрим основные методы расчета результатов испытаний и математические принципы, на которых основаны эти методы;
- Приведем примеры программной реализации методов; Вы можете использовать эти примеры в своих проектах.

Множественные эксперименты: когда и почему
Очевидно, что любое техническое усложнение эксперимента должно быть оправдано практической необходимостью.Это также относится к множественным тестам.
Если аудитория разделена более чем на две подгруппы, вероятность получения ошибки I рода в ходе эксперимента возрастает в геометрической прогрессии:
Где
- количество подгрупп,
— заданный уровень статистической значимости.
Таким образом, добавив к обычному парному тесту всего лишь одну дополнительную подгруппу (
) на заданном стандартном уровне
мы получаем вероятность ошибки I рода
, что значительно превышает заданное нами
.
Зачем проводить многочисленные эксперименты, если они снижают точность результатов исследования? Причин может быть несколько:
- Вы хотите протестировать несколько изменений и их совокупное влияние на показатели продукта.
Пример — показ пользователю на странице сервиса двух новых элементов, расположенных по-разному относительно друг друга.
- Изменения можно тестировать только в течение одного периода времени, поскольку они взаимозависимы и чувствительны к еженедельной сезонности.
Примером может служить отключение рекламных каналов для расчета эффекта межканальной каннибализации.
- Заказчик хочет максимально быстро и дешево получить ответ о том, какой вариант выбрать, при этом сэкономив время на разработке и реализации эксперимента.
Что это такое и как это правильно сделать, речь пойдет ниже.
Множественные эксперименты: особенности расчета
Базовые концепты
Рассмотрим общий случай, когда мы имеем дело сгипотезы
,
о попарном равенстве медианы или среднего
подгруппы.
В этом случае возможны как правильные, так и неправильные результаты.
для каждого
гипотезы.
Представим результаты в виде эксперимента с матрицей путаницы:
| не отклонен |
отклоненный |
|
|
|---|---|---|---|
| истинный |
|
|
|
| неправильный |
|
|
|
| |
|
|
от
отвергли основные гипотезы.
На основе этих параметров мы введем два важных понятия ошибок, которые контролируются при многократном тестировании:
И
.
Вероятность групповой ошибки
Коэффициент семейных ошибок — это вероятность получения хотя бы одной ошибки типа I, которая определяется как:
(False Discovery Rate) – математическое ожидание отношения ошибок I рода к общему числу отклонений основной гипотезы:
Рассмотрим методы контроля этих ошибок на примере стандартного корпуса продукта.
Описание случая
В качестве простого примера рассмотрим эксперимент, в котором трем изолированным, непересекающимся группам пользователей были показаны три версии страницы с просьбой нажать кнопку вызова для получения рекламы.Для удобства расчета в качестве основного показателя возьмем общее количество звонков в каждой группе.
Давайте посмотрим, как менялась исследуемая метрика: 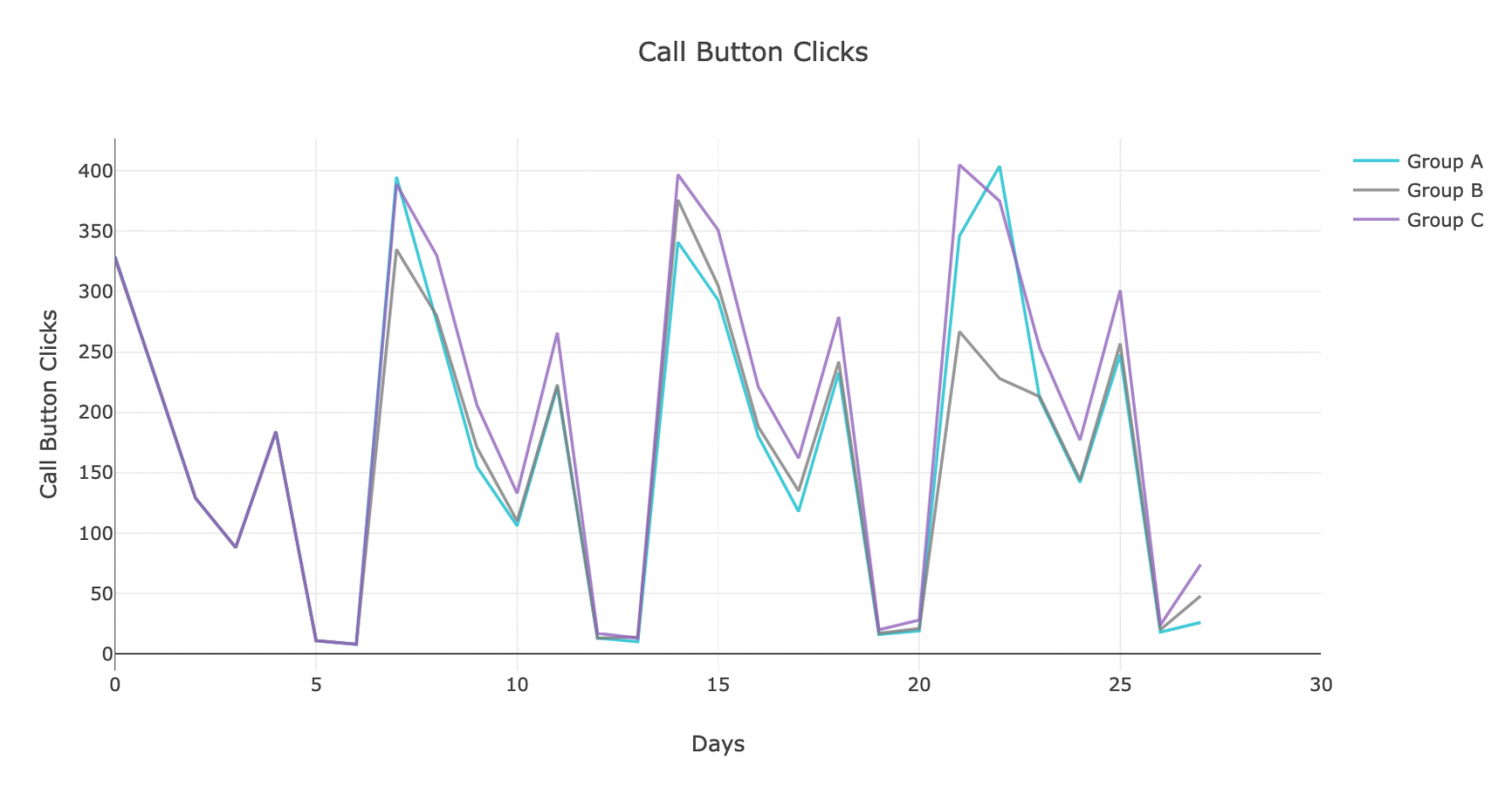
Рис.
1. График динамики кликов по кнопке вызова
Воспользуемся стандартным методом
чтобы привести распределение целевой метрики в выборках к нормальному виду, и посмотреть на гистограммы и диаграммы диапазона средних значений в выборках: 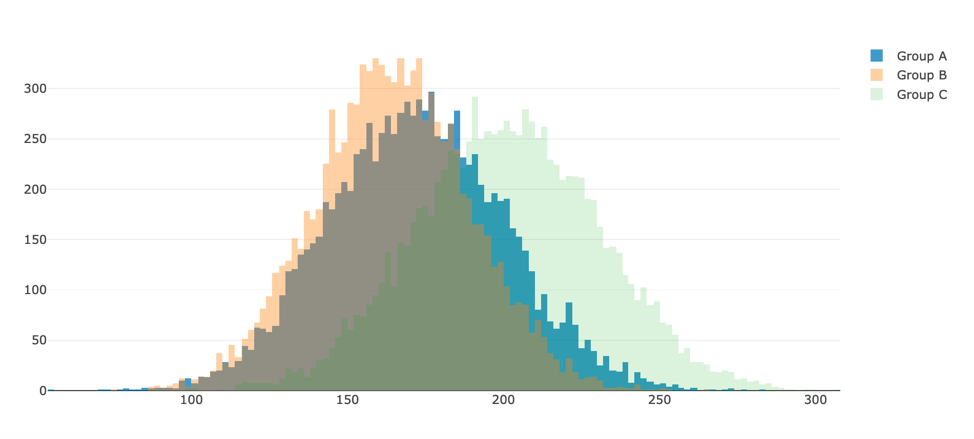
Рис.
2. Гистограмма распределения средних значений по группам 
Рис.
3. Диаграмма размаха средних значений по группам Судя по графикам, группа С выигрывает по количеству нажатий кнопки вызова.
Однако необходимо убедиться, что результаты статистически значимы.
Для этого приведем расчетную метрику к виду нормального распределения и воспользуемся обычным t-критерием Стьюдента для попарного сравнения групп в эксперименте, а затем воспользуемся методами контроля.
И
для учета поправки на множественные сравнения.
ФВЭР-контроль
Существует множество способов борьбы с этой ошибкой, но наиболее распространенными являются два: 1) одноэтапная процедура с одновременной регулировкойдля всех гипотез, проверенных по методу Бонферрони; 2) последовательная итеративная корректировка
с принятием решения на каждом шаге в соответствии с результатом метода Холма.
1. Поправка Бонферрони
Эта одноэтапная процедура снижает вероятность ложноположительного результата эксперимента.
Суть метода заключается в принятии альтернативной гипотезы, если:
Где
— количество проверенных гипотез.
Метод можно довольно просто реализовать с помощью стандартной библиотеки.
:
После получения результатов статистической оценки можно сделать выводы о том, различаются группы или нет. Основной недостаток подхода: чем больше подгрупп, тем ниже мощность критерия, что увеличивает вероятность принятия неверной гипотезы.from bootstrapped import bootstrap as bs from bootstrapped import compare_functions as bs_cmp from bootstrapped import stats_functions as bs_st bs_ab_estims = bs.bootstrap_ab(np.array(group_A), np.array(group_B), bs_st.mean bs_cmp.difference, num_iterations=5000, alpha=0.05/3, iteration_batch_size=100, scale_test_by=1, num_threads=4) bs_bc_estims = bs.bootstrap_ab(np.array(group_B), np.array(group_C), bs_st.mean bs_cmp.difference, num_iterations=5000, alpha=0.05/3, iteration_batch_size=100, scale_test_by=1, num_threads=4) bs_ac_estims = bs.bootstrap_ab(np.array(group_A), np.array(group_C), bs_st.mean bs_cmp.difference, num_iterations=5000, alpha=0.05/3, iteration_batch_size=100, scale_test_by=1, num_threads=4)
Например, для десяти тестов и
нужно получить
сказать, что разница существенная.
Чтобы смягчить эти недостатки, можно выбрать метод Холма.
2. Метод Холма
Это процедура последовательного изменения сверху вниз.
.
На первом шаге алгоритма метода реальные
отсортировано по возрастанию:
затем корректируется изначально указанный
-уровень:
после чего проверяется условие
и делается вывод, верна ли основная гипотеза
.
Точкой останова алгоритма является момент i, когда принимается первая основная гипотеза.
и все последующие
.
Этот метод можно реализовать с помощью процедуры
из библиотеки
с параметром
: from bootstrapped import bootstrap as bs
from bootstrapped import stats_functions as bs_st
from scipy.stats import ttest_ind
from statsmodels.sandbox.stats.multicomp import multipletests
bs_a = bs.bootstrap(np.array(group_A), stat_func=bs_st.mean,
num_iterations=10000, iteration_batch_size=300,
return_distribution=True)
bs_b = bs.bootstrap(np.array(group_B), stat_func=bs_st.mean,
num_iterations=10000, iteration_batch_size=300,
return_distribution=True)
bs_c = bs.bootstrap(np.array(group_C), stat_func=bs_st.mean,
num_iterations=10000, iteration_batch_size=300,
return_distribution=True)
stat_ab, p_ab = stats.ttest_ind(pd.DataFrame(bs_a), pd.DataFrame(bs_b))
stat_bc, p_bc = stats.ttest_ind(pd.DataFrame(bs_b), pd.DataFrame(bs_c))
stat_ac, p_ac = stats.ttest_ind(pd.DataFrame(bs_a), pd.DataFrame(bs_c))
print(sorted([p_ab, p_bc, p_ac]))
print("FWER: " + str(multipletests(sorted([p_ab, p_bc, p_ac]), alpha=0.05,
method='holm', is_sorted = True)))
контроль Рузвельта
Контрольозначает, что условие выполнено
.
В которой
, т.е.
вероятность получения ошибки I рода при контроле
уменьшается.
Метод Беньямини-Хохберга
Эта восходящая процедура предполагает последовательные изменения.
, предварительно отсортированные по возрастанию:
Тогда оригинал
-уровень корректируется по формуле:
затем, как и в методе Холма, проверяется условие
и делается вывод, верна ли основная гипотеза
и все последующие
.
Метод Беньямини-Хохберга, как и метод Холма, можно реализовать с помощью процедуры
: print("FDR: " + str(multipletests([p_ab, p_bc, p_ac], alpha=0.05,
method='fdr_bh', is_sorted = False)))
Заключение
В статье мы рассказали об основных методах оценки результатов множественных тестов и привели примеры программного кода, реализующего эти методы.Надеемся, что вы провели время с пользой и интересом и сможете применить описанные процедуры на практике.
А если у вас возникнут вопросы, мы будем рады на них ответить.
Спасибо за внимание! Теги: #математика #Большие данные #аналитика #анализ данных #Аналитика мобильных приложений #ИТ-статистика #аналитика продуктов #A/B-тестирование #ab-тестирование #Bootstrap

-
Основные Этапы Гибких Методологий
19 Oct, 24 -
Педерсен, Чарльз
19 Oct, 24 -
Резюме Программистов. Часть 1 (Плохая)
19 Oct, 24


