Введение Очень часто как в точных науках (физике, химии), так и в других областях (экономике, социологии, маркетинге и т.п.
) при работе с различного рода экспериментально полученными зависимостями одной величины (Y) от другой (X) Возникает необходимость описать полученные данные некоторой математической функцией.
Этот процесс часто называют выражение , приближение , подход или примерка .
Наиболее распространенная линейная функция, используемая для аппроксимации данных:
Действительно, математически он довольно прост, с ним удобно работать, смысл параметров А и В кристально ясен даже ученику среднего класса, для него существуют отлаженные математические методы, позволяющие однозначно и быстро их определить.
найдено, а главное, множество экспериментально полученных зависимостей от. На самом деле они носят более или менее линейный характер.
Лирическое отступление Важно также отметить ситуацию, когда одни и те же экспериментальные данные могут достаточно хорошо описываться (в рамках заданных метрик) весьма разными математическими функциями, как показано на рис.
1. 
Рис.
1. Попытка описать один и тот же набор экспериментальных данных квадратичными, степенными и линейными функциями.
Однозначного ответа нет, и того, что лучше, не существует. Все определяется теми задачами (получение площади под кривой, выяснение значения производной, выяснение нового значения Y при другом X и т. д.), для решения которых предлагается использовать ту или иную другое математическое приближение.
Конечно, наиболее полезную информацию можно получить из того математического приближения, которое не только прекрасно описывает экспериментальные данные, но и за которым стоит физико-химическая/экономическая и т. д. модель зависимости, наблюдаемой в эксперименте.
Затем из полученных оптимизированных параметров извлекается полезная информация.
Бывают ситуации, когда экспериментально полученная зависимость оказывается более сложной, а использование линейной аппроксимации становится бессмысленным и приходится привлекать другие математические функции, рис.
2-А.
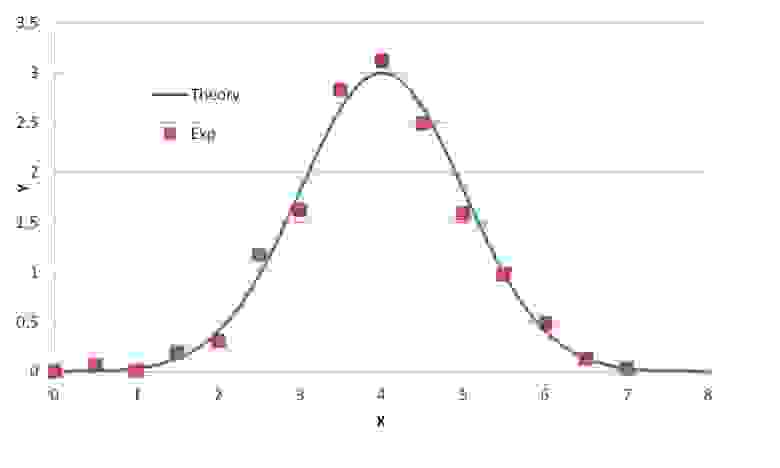
Рис.
2-А.
Абстрактный пример нелинейной экспериментальной зависимости Y от X (красные точки) и ее теоретической аппроксимации (синяя кривая) функцией Гаусса.
Существует ряд программных решений для подгонки нелинейных экспериментальных зависимостей (Matlab, Origin, Datafit и др.
).
Провести такую подгонку в MS Excel (помним про решатель) не очень сложно.
Однако бывают ситуации, когда экспериментальная кривая состоит из нескольких полностью или частично перекрывающихся отдельных кривых, независимых по своей природе.
Особенно часто это проявляется при физических и химических измерениях: инфракрасной спектроскопии (рис.
2-Б), ядерно-магнитном резонансе (рис.
2-В), рентгеновской фотоэлектронной спектроскопии (рис.
2-Г), хроматографии (рис.
2).
-Е) и т. д. В некоторых случаях небольшие, но очень гордый важный пик полностью или почти полностью скрыт большим пиком, так что он почти не виден невооруженным глазом.
И о его существовании приходится догадываться исходя из косвенных соображений.
| Примеры |
|---|
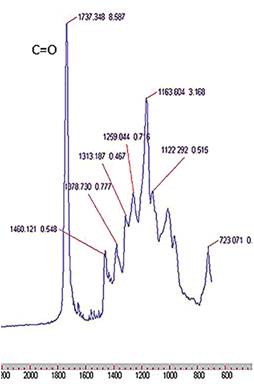 Рис. 2-Б. Пример перекрытия пиков в FTIR-спектре. По оси Y (не показана) — безразмерная величина, характеризующая поглощение ИК-излучения веществом; по оси X — волновое число в см -1 . Источник: Канадский журнал микробиологии 63 (12), октябрь 2017 г. .
|
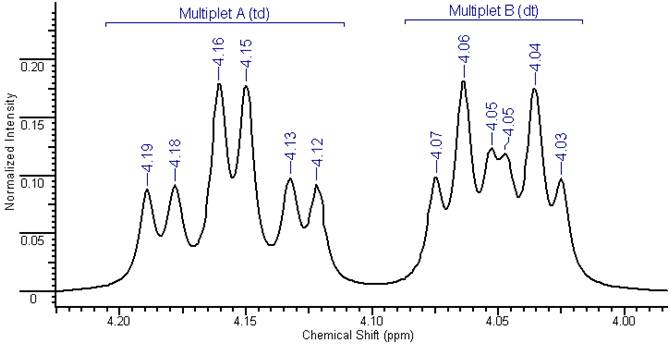 Рис. 2-Б. Пример перекрытия пиков H1-ЯМР. Источник.
|
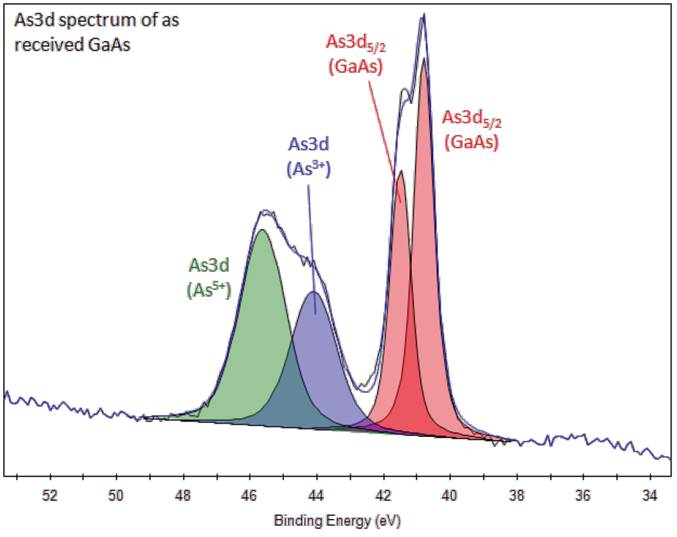 Рис. 2-Г. Перекрытие пиков в спектре As3d-XPS образца арсенида галлия (GaAs). Отчетливо видны различные электронные состояния As в образце. Количественный анализ, выполняемый с помощью фитингов, позволяет исследователям проанализировать структуру образца. Источник .
|
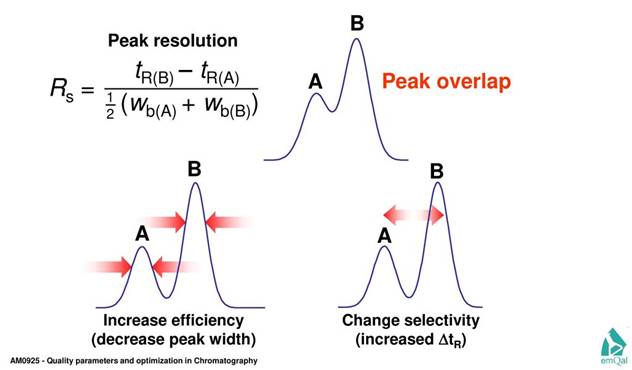 Рис. 2-Д. Примеры перекрытия хроматографических пиков. Концентрация аналита прямо пропорциональна площади под кривой пика, поэтому необходимо уметь точно определить эту площадь. .
|
В ЯМР во время измерения увеличивают напряженность магнитного поля и уменьшают температуру, что приводит к разделению (разрешению) пиков.
Иными словами, они используют аппаратно-методическое решение задачи, что, несомненно, хорошо в контексте совершенствования приборов и технологий, но зачастую стоит больших денег и не всегда доступно.
В инфракрасной спектроскопии они мало что делают с плохо разделенными пиками; аппаратно их разделить невозможно, и исторически все привыкли к тому, что тот или иной пик представлен на спектре, например, как плечо на фоне другого пика, и довольно редко кто-то пытается извлечь более полную информацию из такого спектра путем его подгонки (J. Braz. Chem. Soc., Vol. 19, № 8, 1582-1594, 2008).
В то же время в рентгеновской фотоэлектронной спектроскопии практически всегда необходимо подогнать экспериментальные данные в виде суперпозиции нескольких отдельных пиков (имеющих форму кривой Гаусса), что реализуется с помощью специального программного обеспечения.
поставляется вместе с устройством.
Для разделения пиков в жидкостной и газовой хроматографии уменьшают концентрации веществ, устанавливают дополнительные разделительные колонны, увеличивают их длину, применяют методы химической модификации веществ, изменяют условия хроматографического разделения и т. д. Но, как ни странно Несмотря на актуальность проблемы, прогресса в этой области использования математических возможностей разделения пиков нет. Хотя есть соответствующие методы И модели , но они пока не нашли своего применения в коммерческих хроматографических решениях.
Несмотря на возникающую необходимость проведения многокомпонентной (многофункциональной) подгонки, автор этих терминов не знаком с программным обеспечением, позволяющим использовать для подгонки одновременно несколько одинаковых или разных математических функций.
В замечательной программе OriginPro 8 мультиподгонка ограничена функциями Лоренца и Гаусса, что неплохо, но недостаточно.
При этом качество примерки не всегда является удовлетворительным и нет возможности контролировать сам процесс примерки.
Если результаты не нравятся, то придется начинать процесс с самого начала и столько раз.
Еще одним важным моментом является тот факт, что почти все программы при выполнении подгонки работают только с этим сигналом Y и не подгоняют автоматически производную этого сигнала, что может привести к незначительным результатам.
Поэтому, когда возникла реальная задача описания экспериментальных кривых, по форме которых было понятно, что без многофункциональной фитинга обойтись невозможно, подходящего инструмента под рукой не оказалось.
Также хотелось ясности и управляемости процесса подгонки, совпадения экспериментальных и расчетных производных.
Конечно, задачу можно было решить вручную в MS Excel, но данных было много, и мне хотелось попрактиковаться в Python, который я начал изучать несколькими месяцами ранее как свой первый язык программирования.
В связи с этим была поставлена следующая цель.
Цель
Написать программу для удобной, наглядной, быстрой и качественной мультиподгонки загруженных экспериментальных данных с учетом подгонки самого сигнала и его производной.В этом случае пользователь должен вручную задать количество различных математических функций, используемых при настройке, и иметь возможность выбрать ту или иную математическую функцию из списка.
В процессе самой подгонки хотелось иметь возможность самому контролировать процесс подбора параметров, а не слепо доверять алгоритмам оптимизации, в первую очередь из-за того, что они не учитывают совпадение производных экспериментального и расчетного сигналов.
.
Плюс другие мелочи, такие как сглаживание шума и удаление из исходных данных «артефактов», мешающих вычислению производной.
Результаты
Учитывая отсутствие опыта программирования, задача показалась не простой, но очень интересной, которую пришлось решить, разбив ее на подзадачи:- Чтение/запись данных;
- Преобразование неудобного формата значений даты и времени «17.07.2019 14:55:38» в удобные относительные минуты;
- Изучите основы Matplotlib для построения графиков данных и динамического изменения параметров функций с помощью встроенного гаджета.
Очень полезно Веб-сайт ;
- Применение простого (5-точечного) метода сглаживания и замены найденных в массиве данных дубликатов (по оси X) соответствующей линейной аппроксимацией;
- Численное интегрирование и дифференцирование данных;
- Создание графического интерфейса и изучение для этого основ ООП.
Подробности в самом коде, код доступен здесь .
Большинство вопросов и задач оказались стандартными, полное или частичное решение которых было найдено на различных сайтах и книгах, посвященных Python, а также на переполнение стека .
Решения и примеры тупо скопировал поняты и адаптированы к их потребностям.
Ниже мы кратко опишем работу программы, ее возможности и ограничения на данный момент. Программа состоит из трех рабочих файлов и краткой инструкции: Fitting_tool.py -Интерфейс, проверка правильности ввода параметров, вызов различных функций.
NumPy1.py — Класс методов чтения, записи, обработки данных и их графического отображения.
ThFunction.py — Класс нескольких математических функций, их параметров с начальными значениями и границами интервалов изменения этих параметров.
Инструмент для установки v.1.0 Help.pdf — Небольшой мануал с картинками, который я решил сделать сразу на английском языке.
При запуске программы вам будет предложено открыть файл с вашими данными или использовать существующие примеры, которые необходимо импортировать.
Затем вы можете просмотреть исходный график и его производную, рассчитанную как есть или после математического сглаживания.
При этом заранее сказать, какой метод сглаживания будет работать лучше, непросто и имеет смысл попробовать их все или выбрать вариант без сглаживания.
В результате появится стандартное окно с графиком экспериментального сигнала и его производной, рис.
3-А.
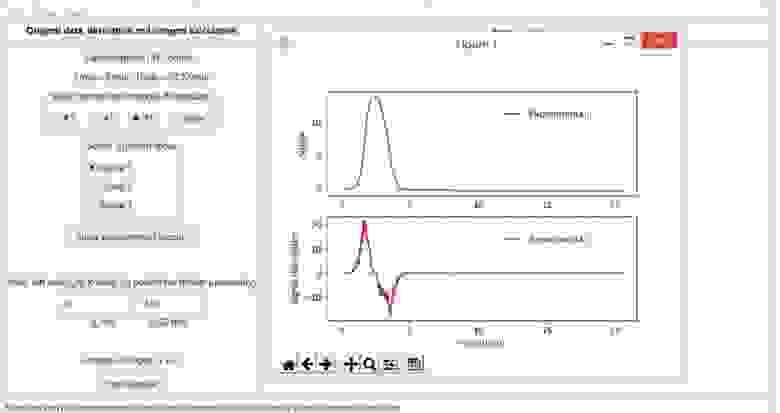
Рис.
3-А.
Графическое представление исходного экспериментального сигнала и его производной с использованием одного из трех методов математического сглаживания.
Задав левую и правую границы рассматриваемого интервала, можно ориентировать график и последующие расчеты на интересующую область, Рис.
3-Б.
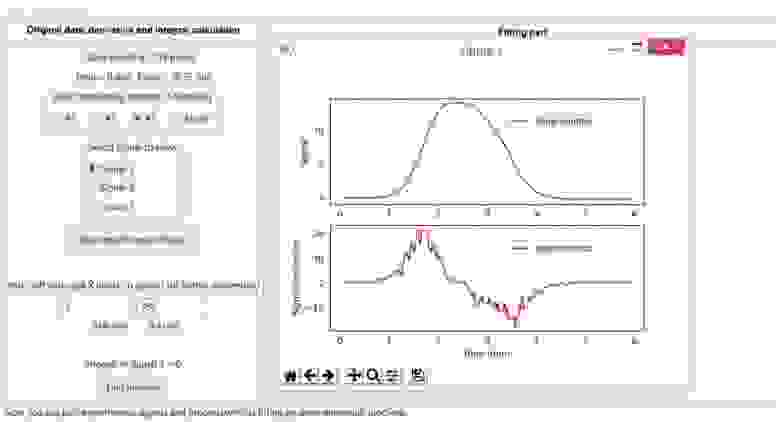
Рис.
3-Б.
Установка левой и правой границ интервала наиболее интересного участка экспериментальной кривой для дальнейшей подгонки.
В правой части программы вы можете установить количество математических функций, используемых для подгонки, и выбрать тип каждой используемой функции.
После этого вы сможете установить три значения для каждого параметра выбранной функции.
Значения Min, Max соответствуют левой (Min) и правой (Max) границам числового интервала, в котором пользователь будет искать оптимальное значение параметра.
Значение Def (мин.
< Def < Max) shows the initial, which is also the current value of this parameter, Fig. 4. 
Рис.
4. Выберите количество и тип математических функций, которые будут использоваться для подгонки.
При необходимости пользователь может изменить значения Min, Max и Def для каждого из параметров каждой функции.
Далее либо, оставаясь в рамках одной выбранной функции, пользователь может осуществить подгонку (Локальную подгонку) ее параметров, либо через меню Подгонка\Глобальная подгонка оптимизировать параметры глобальной функции, представляющей собой суперпозицию двух (или более) локальных функций.
Для начала удобно «обнулить» амплитуду второй функции и добиться некоторого (не обязательно идеального) совпадения профилей левой (или правой) части экспериментального сигнала и его производной с соответствующей частью первая функция и ее производная, рис.
5-А.
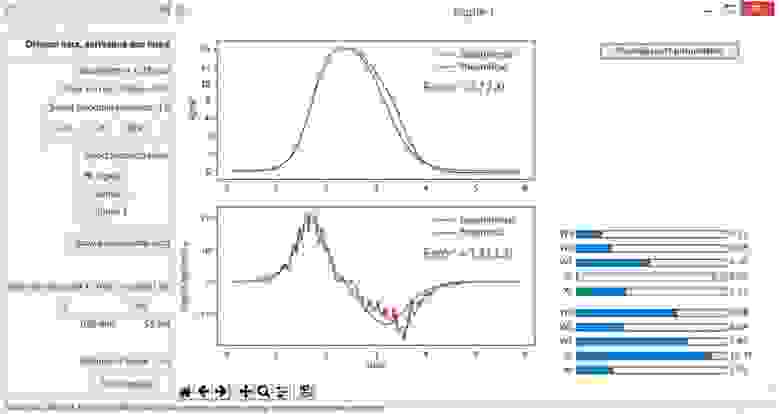
Рис.
5-А.
Установка с одной функцией.
Попытка получить наилучшее соответствие левой части экспериментальной кривой.
Амплитуда второй функции специально уменьшена практически до нуля.
После получения удовлетворительного результата «включаем в игру» вторую функцию (рис.
5-Б) и находим для нее оптимальные параметры.
Во время его примерки можно вернуться к параметрам 1. й функции и убедитесь, что ошибка находится на глобальном минимуме для всех ее параметров.
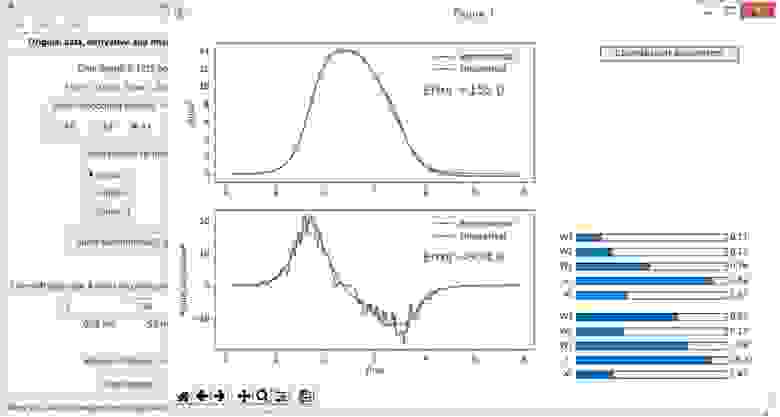
Рис.
5 B. Подбор двух функций дает лучшее описание исходного сигнала и его производной (игнорируя оставшийся шум на графике производной).
Кнопка «Закрыть и экспортировать параметры» позволяет закрыть окно с графиком и экспортировать текущие параметры в главное окно программы, где можно установить более удобные значения Min и Max для выбранных параметров и снова продолжить уменьшать ошибку за счет Подгонка\Глобальная подгонка.
Ошибка, которая также является метрикой качества аппроксимации исходного сигнала и его производной, определяется по стандартной формуле:
где ЮВ я и СТ я экспериментальные и расчетные значения сигналов.
N — количество точек в массиве, для удобства выбран множитель 1000. Аналогичная формула используется для оценки точности аппроксимации производной сигнала, однако из-за наличия возможных шумов полностью «обнулить» ее не удастся, да это и не обязательно, поскольку совпадение профилей кривых достаточно.
Если для качественной примерки двух функций недостаточно, то можно сбросить настройки кнопкой «Сброс» и выбрать дополнительные функции.
На данный момент программа предоставляет шесть математических функций:
|Сокращение | Название | Формула и параметры | Пример графика |
|---------------|------------|----------------------------|------------------|
| ДбСигмоинд | Двойная сигмовидная |
Параметры: A, Xc, W1, W2 и W3| |
|Синус|Синус |
Параметры: A, w и phi||
|Гаусс|Функция Гаусса|
Параметры: A, b и c||
|Exp|Ээкспоненциальная функция|
Параметры: A и b||
|Лоренц|Функция Лоренца|
Параметры: А, х 0 ||
|Сигмовидная|Сигмовидная|
Параметры: A, B и C|
|
На этом было решено остановиться и ограничить версию 1.0 этими шестью математическими функциями.
Желающие могут легко добавить новую математическую функцию в файл ThFunction.py и добавить условие определения ее параметров в функцию «F_Option» файла Fitting_tool.py, используя готовые шаблоны из комментариев в файлах.
В будущих версиях, если будет интерес к этой теме, я постараюсь добавить возможность ввода пользователем собственных математических функций в саму программу.
###Выводы Создан удобный инструмент, позволяющий мультифитировать экспериментальные данные в ручном режиме, одновременно контролируя не только форму и погрешность расчетного сигнала, но и форму и погрешность его производной.
Работа над проектом принесла огромное удовольствие и позволила получить первый практический опыт программирования.
Хочется надеяться, что созданный инструмент Fitting окажется действительно полезным кому-нибудь еще.
Теги: #python #наука о данных #python #подгонка #приближение #подгонка данных
-
Отправка Url-Адреса Вашего Веб-Сайта
19 Oct, 24 -
Кто В Твоей Банде?
19 Oct, 24 -
Amd Катализатор 9.1
19 Oct, 24 -
Концептуальная Безопасность
19 Oct, 24 -
Google Просмотр Улиц, Версия 1907.
19 Oct, 24 -
Грааль И Трюфель
19 Oct, 24


