Методы Регрессионного Анализа В Data Science

На графике выше вы можете видеть, что есть определенная переменная x и определенная переменная y, и мы наблюдаем значения y в определенном x. Мы знаем эти точки и знаем их координаты, а также знаем, что x каким-то образом влияет на y, то есть эти две переменные зависят друг от друга.

Естественно, мы хотим рассчитать уравнение их зависимости – для этого воспользуемся модель классическая попарная линейная регрессия , когда предполагается, что их зависимость может быть описана некоторой прямой линией.

Соответственно, коэффициенты прямой затем выбираются так, чтобы минимизировать ошибку описания данных.

И от того, какая ошибка (метрика качества) выбрана, зависит реальный результат построения линейной регрессии.

Еще одной задачей анализа данных является рекомендательные системы .

Это когда мы говорим, что есть, например, интернет-магазины, в них есть определенный набор товаров, и человек совершает покупки.

На основе этой информации можно представить описание этого человека в векторном пространстве и, построив это векторное пространство, в дальнейшем построить математическую зависимость вероятности, с которой этот человек купит тот или иной товар, зная свой предыдущий покупки.

Соответственно, речь идет о классификации, когда мы классифицируем потенциальных покупателей по принципам: «купил бы или не купил», «интересно или не интересно» и т. д. Существуют разные подходы: пользовательский и предметный.

Третья зона - компьютерное зрение .

В ходе выполнения этой задачи мы пытаемся определить, где находится интересующий нас объект. Фактически это решение проблемы минимизации ошибок за счет выбора конкретных пикселей, формирующих изображение объекта.

Во всех трёх задачах есть оптимизация, минимизация ошибок и наличие той или иной модели, описывающей зависимость переменных.

Причём внутри каждого лежит представление данных, которое раскладывается в векторное описание.

В нашей статье мы уделим особое внимание разделу, который затрагивает конкретно регрессионные модели .

Мы уже упоминали, что существует некий набор пар данных: X и Y. Мы знаем, какие значения Y принимает относительно X. Если X — это время, то мы получаем модель временных рядов, в которой Y — это, скажем, цена нефти и одновременно курс рубля к доллару, а Х — определенный период времени с 2014 по 2018 год: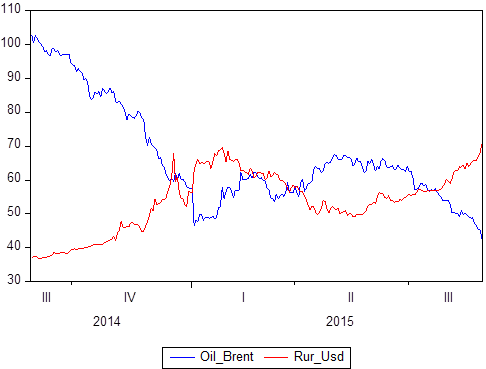



Если вы изобразите это графически, вы увидите, что эти два временных ряда зависят друг от друга.

Определив понятие корреляции, вы можете вычислить степень их зависимости, а затем, если вы знаете, что некоторые величины прекрасно коррелируют (корреляция равна 1 или -1), вы можете использовать это либо для задач прогнозирования, либо для задач описания.

.

Рассмотрим следующую иллюстрацию:



Самое сложное при формировании регрессионной модели — это изначально поместил в свою память какую-то конкретную функцию .

Например, для рисунка А это Y = kX + b, для B это Y = -kX + b, на рисунке B «y» равен какому-то числу, график на рисунке D скорее всего основан на корне «x» базис D, возможно, является параболой, а базис E — гиперболой.

Оказывается, мы выбираем какую-то модель зависимости данных , а виды зависимости между случайными величинами различны.

Все не так очевидно, ведь даже на этих простых рисунках мы видим различные зависимости.

Выбрав конкретную взаимосвязь, мы можем использовать методы регрессии для калибровки модели.

Качество ваших прогнозов будет зависеть от того, какую модель вы выберете.

.

Если мы ориентируемся на модели линейной регрессии, то предполагаем, что существует определенный набор реальных значений:



На рисунке показаны 4 наблюдаемых значения Х1, Х2, Х2, Х4. Для каждого из «иксов» известно значение Y (в нашем случае это точки: P1, P2, P3, P4).

Это точки, которые мы фактически наблюдаем в данных.

Таким образом, мы получили некий набор данных.

И по какой-то причине мы решили, что линейная регрессия лучше всего описывает отношения между «X» и «Y».

Тогда весь вопрос в том, как построить уравнение прямой Y = b ₁ + б ₂ X, где б ₂ — коэффициент наклона, b ₁ — коэффициент пересечения.

Весь вопрос в том, что б ₂ и б ₁ Лучше всего обеспечить, чтобы эта прямая линия как можно точнее описывала взаимосвязь между этими переменными.

R-баллы ₁ , Р ₂ , Р ₃ , Р ₄ — это значения, которые наша модель выдаёт для значений X. Что происходит? Точки P — это точки, которые мы реально наблюдаем (фактически собранные), а точки R — это точки, которые мы наблюдаем в нашей модели (те, которые она производит).

Далее следует безумно простая человеческая логика: модель будет считаться качественной тогда и только тогда, когда точки R расположены максимально близко к точкам P .

Если мы построим расстояние между этими точками для одинаковых «Х» (P ₁ - Р ₁ , П ₂ - Р ₂ и т. д.), то мы получаем так называемые ошибки линейной регрессии.

Мы получим отклонения в линейной регрессии, и эти отклонения называются U. ₁ , У ₂ , У ₃ …У _н .

И эти ошибки могут быть как положительными, так и отрицательными (мы могли их переоценить или занизить).

Чтобы сравнить эти отклонения, их необходимо проанализировать.

Здесь использован очень большой и красивый метод – возведение в квадрат (возведение в квадрат «убивает» знак).

А сумма квадратов всех отклонений в математической статистике называется RSS (Residual Sum of Squares).

Путем минимизации RSS с помощью b ₁ и минимизация RSS с помощью b ₂ , мы получаем оптимальные коэффициенты, которые фактически выводятся метод наименьших квадратов .

После построения регрессии мы определили оптимальные коэффициенты b ₁ и б ₂ , и у нас есть уравнение регрессии, проблемы на этом не заканчиваются, а проблема продолжает развиваться.

Дело в том, что если отметить саму регрессию, все значения, которые у нас есть, а также средние значения «игр» на одном графике, то суммы квадратов ошибок можно дополнительно уточнить.

При этом считается полезным отображать ошибки прогнозирования регрессии относительно переменной X. См.

рисунок ниже: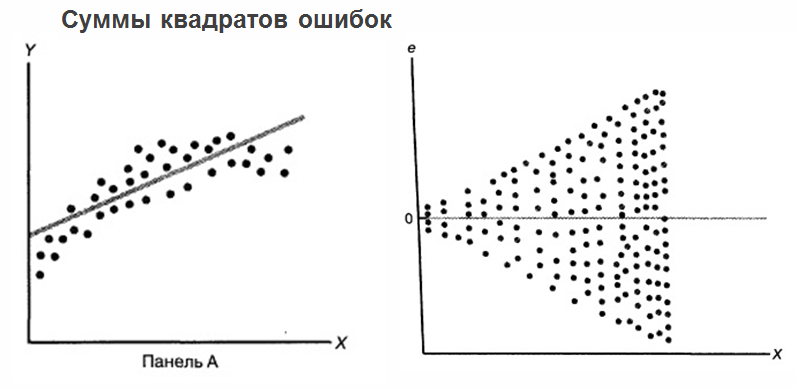



Мы получили некую регрессию и нанесли на график реальные существующие данные.

Мы получили расстояние от каждого приведенного значения до регрессии.

И мы рисовали его относительно нулевого значения для соответствующих значений X. А на рисунке выше мы на самом деле видим очень плохую картину: ошибки зависят от X .

Определенно выражена некоторая корреляция: чем дальше по «Х» мы движемся, тем больше значение ошибок .

Это очень плохо.

Наличие корреляции в данном случае свидетельствует о том, что мы ошибочно взяли регрессионную модель, и был какой-то параметр, о котором мы «не подумали» или просто упустили из виду.

Ведь если все переменные поместить внутрь модели, ошибки должны быть полностью случайными и не должны зависеть от того, чему равны ваши факторы.

Ошибки должны иметь одинаковое распределение вероятностей.

, иначе ваши прогнозы окажутся неверными.

Если вы нарисовали на плоскости ошибки своей модели и столкнулись с расходящимся треугольником, лучше начать с нуля и полностью пересчитать модель.

Анализируя ошибки, можно даже сразу понять, где вы просчитались и какого рода ошибку допустили.

И здесь нельзя не упомянуть теорему Гаусса-Маркова:



Теорема определяет условия, при которых оценки, полученные нами методом наименьших квадратов, будут лучшими, непротиворечивыми и эффективными в классе линейных несмещенных оценок.

Вывод можно сделать следующий: теперь мы понимаем, что область построения регрессионных моделей в некотором смысле является кульминацией математики.