Недавно я был на хабе статья , в котором описывалось, как можно определить, где находится точка по отношению к многоугольнику: внутри или снаружи.
Подобная проблема встречается довольно часто при геометрическом моделировании и компьютерной графике.
А так как описанный в статье метод был несколько неоптимален, а в комментариях был небольшой хаос, возникла идея написать эту статью.
Итак, какие алгоритмы существуют в современной компьютерной графике для определения принадлежности данной точки многоугольнику или нет. Прежде чем начать, хочу сразу описать проблему.
Хотя сама задача проста: нам дан набор точек и задан порядок соединения этих точек.
И дается балл, что мы проверяем на членство.
Предполагается, что наш многоугольник замкнут, и в общем случае края многоугольника не пересекаются друг с другом, то есть он свободен от самопересечений.
Ограничений на количество вершин нет, то есть можно легко указать многоугольник с миллионом вершин.
Мы надеемся, что пользователь не спросит нас о чем-то непонятном, но и гарантировать этого мы не можем.
И еще один нюанс: поскольку мы работаем с компьютерной графикой, а значит, используем арифметику с плавающей запятой, которая хоть и позволяет достаточно точно оперировать числами, но все же не лишена ошибок.
Ну вот с проблемой мы вроде бы определились, давайте теперь посмотрим, какие существуют способы решения.
Метод 1: трассировка лучей
Начну с того, что считается самым популярным в мире графики и игр: трассировка лучей.Кратко алгоритм можно описать следующим образом:
- Из проверяемой точки выпускаем луч либо в заданном, либо в произвольном направлении.
- Считаем количество пересечений с многоугольником.
- Если число пересечений четное, мы снаружи.
Если количество пересечений нечетное, мы внутри.
В простейшем случае вам придется пересечь луч всеми отрезками; при использовании деревьев (квадратичных, двоичных или BVH) это число можно уменьшить.
В общем случае алгоритмическая сложность этого алгоритма равна O(log n), где n — количество ребер в многоугольнике.
Способ простой, но, к сожалению, в общем случае им лучше не пользоваться.
Причиной этого является случай, когда мы пересекаем лучом вершину многоугольника или ребро, частично совпадающее с лучом.
Я иллюстрирую это примером.
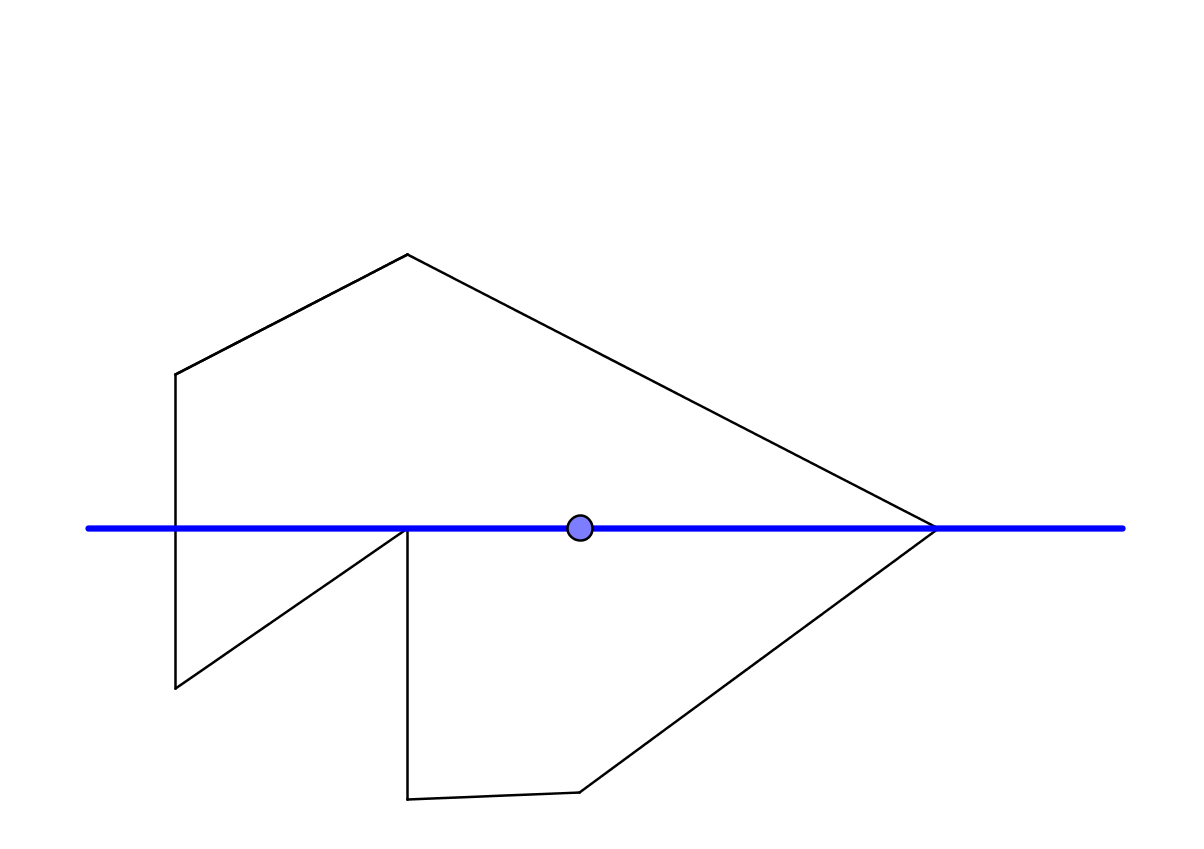
Допустим, у нас есть многоугольник и есть точка.
В самом начале мы договорились, что направление будет по оси x. Мы запускаем луч из точки в положительном направлении оси X, и луч безопасно пересекает многоугольник в вершине.
Возникает вопрос, как именно нам проверить такую ситуацию? Не забывайте, что мы работаем с числами с плавающей запятой и возможны небольшие ошибки.
Перенесемся в мир аналитической геометрии, чтобы мы могли оперировать не просто геометрическими понятиями, но и числами.
Уравнение каждого сегмента (грани многоугольника): а + т( б — а ), Где А – координаты одного конца отрезка, б – координаты другого конца отрезка.
Очевидно, что если луч пересекает отрезок, t должно находиться в интервале [0,1].
Если мы пересекаем вершину лучом, то t = 0 или t = 1. Это в идеальном мире математики.
В реальном мире компьютерной алгебры вы можете получить что-то вроде t = 1e-10. Или t = -1e-10. Или 0,99999999999998. Или 1.000000000000001. Поскольку пересечение двух линий предполагает процедуру деления, это может легко произойти.
Так что же делать в этом случае? Доверьтесь компьютеру и предположим, что если мы строго больше или равны нулю или строго меньше или равны единице, то мы считаем это пересечением, а иначе мы его не считаем? Поверили и получили ситуацию, когда с одним ребром параметр t=-1e-20, с другим ребром t=1.0000000000000000001. В результате мы не считаем это пересечениями, а наш луч благополучно проскочил мимо и результат оказывается неверным.
Давайте посмотрим в другом направлении.
Направил луч в отрицательном направлении.
Там тоже не очень хорошо — луч пересекает вершину внутри многоугольника.
Это также может быть что угодно.
Вместо горизонтального направления взять вертикальное? Никто не гарантирует, что вы не пересечете вершину еще раз.
В примере, который я специально выбрал выше, точка выбрана таким образом, чтобы ее пересечение с лучом, параллельным оси Y и идущим сверху вниз, также пересекало многоугольник в вершине.
Более того, если вы считаете, что пересечение с вершиной — это плохо, посмотрите, что еще может произойти: 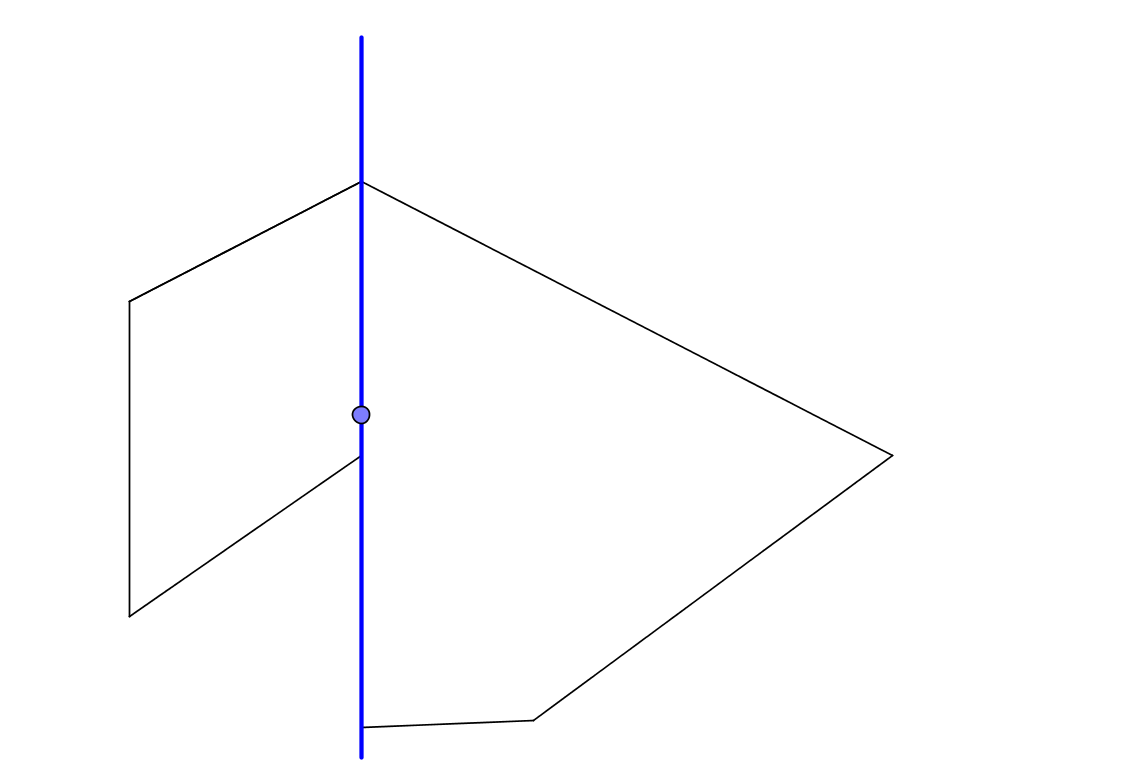
Здесь мы пересекаем луч с отрезком, совпадающим с этим лучом.
Что делать в этом случае? А если не совпадает, но почти совпадает? Представьте себе, что в многоугольнике много почти вырожденных ребер, как при этом пересечься? Самое печальное во всей этой ситуации то, что нам кажется: «Мне нужно что-то очень простое для моих простых целей, меня эта ситуация не коснется».
По закону Мерфи, к сожалению, именно такая ситуация возникает тогда, когда вы меньше всего этого ожидаете.
И вот я плавно перехожу ко второму способу.
Способ 2. Ближняя точка и ее нормаль
Вообще у этого метода ужасное название: псевдонормали, взвешенные по углам, и оно связано с понятием так называемых знаковых полей расстояний.Но я не хочу никого лишний раз пугать, поэтому давайте просто иметь ближайшую точку и ее нормаль (то есть перпендикулярный вектор).
Алгоритм в этом случае следующий:
- Для тестируемой точки мы ищем ближайшую точку на многоугольнике.
При этом помним, что ближайшая точка может находиться не только на отрезке, но и в вершине.
- Ищем нормаль ближайшей точки.
Если ближайшая точка лежит на ребре, то нормалью является вектор, перпендикулярный краю и смотрящий наружу многоугольника.
Если ближайшая точка — одна из вершин, то нормаль — это усредненный вектор ребер, прилегающих к вершине.
- Вычисляем угол между нормалью ближайшей точки и вектором от проверяемой точки к ближайшей.
Если угол меньше 90 градусов, то мы внутри, иначе – снаружи.
Если оно положительное, то оно внутри, если отрицательное, то оно снаружи.
А поскольку нас интересует только знак косинуса, мы, по сути, вычисляем знак скалярного произведения двух векторов.
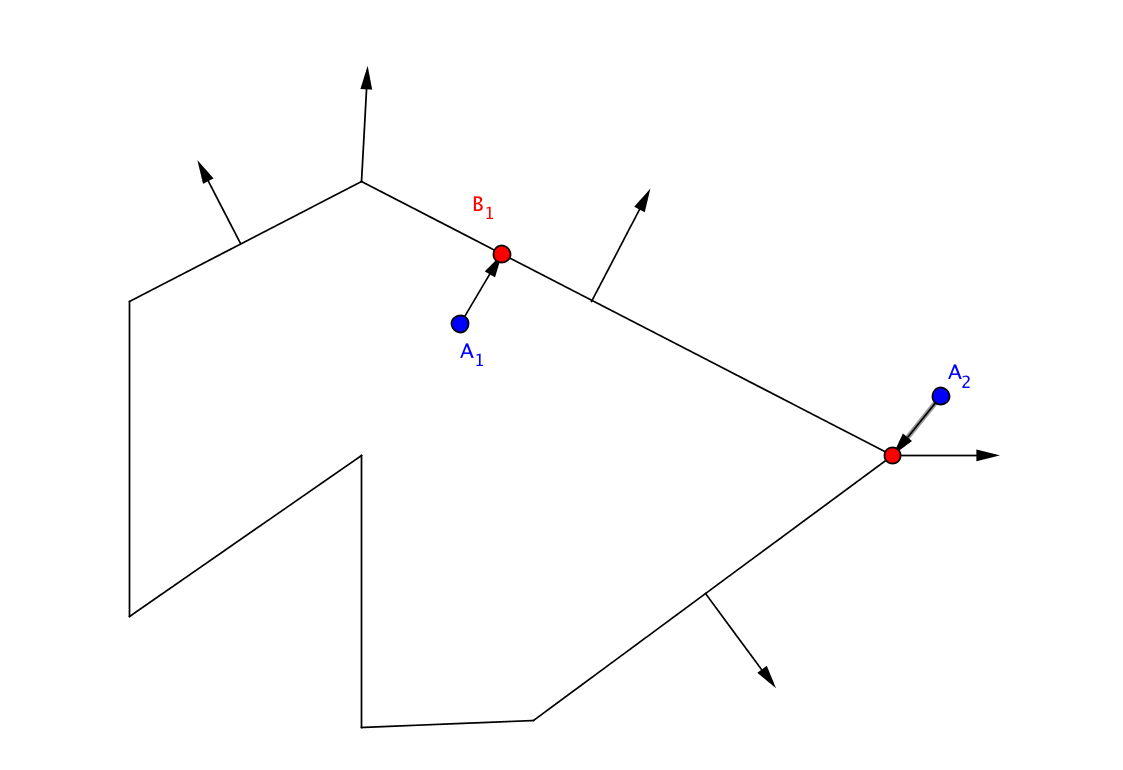
Давайте посмотрим на пример.
Точка А1, ближайшая к ней точка находится на ребре.
Если мы все делаем правильно, нормаль к ребру будет параллельна вектору от проверяемой точки к ближайшей.
В случае точки А1 угол между векторами = 0. Или почти нулевой, так как за счёт операций с плавающей запятой возможно всё.
Менее 90 градусов, контрольная точка A1 находится внутри.
Давайте проверим точку А2. Ближайшей его точкой является вершина, нормаль к которой является средней нормалью ребер, прилегающих к этой вершине.
Мы считаем скалярное произведение двух векторов отрицательным.
Мы снаружи.
Итак, кажется, мы разобрались с сутью метода.
А как насчет проблем с производительностью и плавающей запятой? Как и в случае с трассировкой точек, производительность равна O(log n), если вы используете деревья для хранения информации о ребрах.
С вычислительной точки зрения метод хоть и имеет схожую сложность, но будет несколько медленнее, чем трассировка.
Прежде всего потому, что расстояние между точкой и ребром — чуть более затратная операция, чем пересечение двух линий.
При использовании этого метода возникают проблемы с плавающей запятой, обычно вблизи краев многоугольника.
Причём, чем ближе мы к краю, тем больше вероятность неправильного определения знака.
К счастью, чем ближе мы к краю, тем короче расстояние.
То есть, если мы, например, скажем, что если результирующее расстояние меньше заданного минимума (это может быть константа типа DBL_EPSILON или FLT_EPSILON), то точка принадлежит ребру.
А если оно принадлежит ребру, то мы сами решаем, является ли его ребро частью многоугольника или нет (как правило, оно является частью).
При описании предыдущего метода довольно много говорилось о недостатках.
Пришло время назвать несколько недостатков этого метода.
Прежде всего, этот метод требует, чтобы все нормали кромок указывали в правильном направлении.
То есть, прежде чем определить, снаружи мы или внутри, нам нужно проделать некоторую работу по вычислению этих нормалей и их правильной ориентации.
Очень часто, особенно когда входные данные представляют собой большой дамп вершин и ребер, этот процесс не всегда прост. Если вам нужно определить только одну точку, обычный процесс ориентации может занять много времени, которое можно было бы потратить на что-то другое.
Также этот метод очень не любит, когда на входе — многоугольник с самопересечениями.
Вначале я сказал, что наша задача не рассматривает такой случай, но если бы он был рассмотрен, то этот метод мог бы дать совершенно неочевидные результаты.
Но в целом метод неплох, особенно если у нас на входе многоугольник с большим количеством вершин и ребер и нам нужно проверить множество точек на принадлежность.
Если точек мало, трассировка лучей нестабильна, а хочется чего-то более-менее надежного, то есть третий способ.
Способ 3: Индекс точки относительно многоугольника
Этот метод известен уже довольно давно, но остается во многом теоретическим, главным образом потому, что он не так эффективен, как два предыдущих.Вот ее суть «на пальцах».
Возьмем единичный круг с центром в контрольной точке.
Затем проецируем на этот круг каждую вершину многоугольника лучами, проходящими через вершину и тестируемую точку.
Что-то вроде этого: 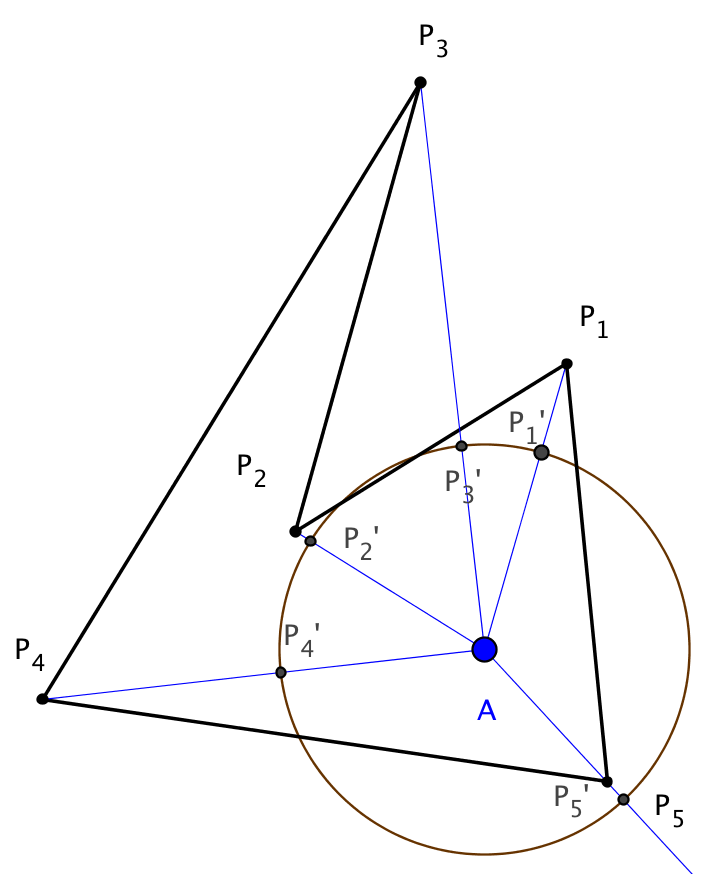
На рисунке точки P1, P2 и так далее являются вершинами многоугольника, а точки P1’, P2’ и так далее – их проекциями на окружность.
Теперь, когда мы смотрим на край многоугольника, по проекциям мы можем сказать, происходит ли вращение против часовой стрелки или по часовой стрелке при движении от одной вершины к другой.
Вращение против часовой стрелки будет считаться положительным вращением, а вращение по часовой стрелке будет считаться отрицательным вращением.
Угол, соответствующий каждому ребру, — это угол между отрезками окружности, проходящими через проекции вершин этого ребра.
Поскольку наше вращение может быть положительным или отрицательным, угол может быть положительным или отрицательным.
Если затем сложить все эти углы, сумма должна быть +360 или -360 градусов для точки внутри и 0 для точки снаружи.
Плюс-минус здесь не просто так.
Если при указании порядка обхода многоугольник обходит против часовой стрелки, результат должен быть +360. Если порядок перемещения ребер многоугольника — против часовой стрелки, то результат равен -360. Чтобы избежать числовых ошибок, обычно поступают так: полученную сумму делят на 360 и доводят до ближайшего целого числа.
Полученное число, кстати, и является индексом точки.
Результат может быть одним из трех: -1 означает, что мы находимся внутри и обходим многоугольник по часовой стрелке, 0 означает, что мы снаружи, +1 означает, что мы снаружи.
Все остальное означает, что мы где-то допустили ошибку или входные данные неверны.
Алгоритм в этом случае следующий:
- Установите сумму углов на 0.
- Для всех ребер многоугольника:
- С помощью скалярного произведения вычисляем угол, образованный векторами, начинающимися в проверяемой точке и заканчивающимися на концах ребра.
- Вычисляем векторное произведение этих самых векторов.
Если его z-компонента положительна, мы добавляем угол к сумме углов, в противном случае мы вычитаем его из той же суммы.
Последнее маловероятно, но вдруг.
Округлите результат до ближайшего целого числа.
+1 или -1 означает, что мы внутри.
0 означает, что мы снаружи.
Давайте посмотрим на пример.
Имеется многоугольник, порядок которого установлен против часовой стрелки.
Есть точка А, которую мы тестируем.
Для тестирования сначала вычисляем угол между векторами AP1 и AP2. На нас смотрит векторное произведение этих самых векторов, а значит, мы прибавляем к сумме.
Двигаемся дальше и посчитаем угол между AP2 и AP3. На нас смотрит векторное произведение, вычитаем полученный угол.
И так далее.
Для этого конкретного рисунка я все рассчитал и вот что получилось: Точка А.
(AP1, AP2)=74,13, (AP2, AP3)=51,58, (AP3, AP4)=89,99, (AP4, AP5)=126,47, (AP5, AP1)=120,99. сумма=74,13-51,58+89,99+126,47+120,99=360. 360/360=1 балл – внутри.
Точка Б.
(БП1, БП2)=44,78, (БП2, БП3)=89,11, (БП3, БП4)=130,93, (БП4, БП5)=52,97, (БП5, БП1)=33,63. сумма=-44,78+89,11-130,93+52,97+33,63=0. Дело снаружи.
И традиционно опишем плюсы и минусы такого подхода.
Начнем с минусов.
Метод прост математически, но не столь эффективен с точки зрения производительности.
Во-первых, его алгоритмическая сложность равна O(n) и, как ни крути, все ребра многоугольника придется перебирать.
Во-вторых, для вычисления угла вам придется использовать операцию арккосинуса и две корневые операции (формула скалярного произведения и ее связь с углом в помощь тем, кто не понимает почему).
Эти операции очень затратны по скорости, к тому же связанные с ними ошибки могут быть существенными.
И в-третьих, алгоритм не определяет напрямую точку, лежащую на ребре.
Либо снаружи, либо внутри.
Третьего не дано.
Однако последний недостаток легко определяется: если хотя бы один из углов равен (или почти равен) 180 градусам, это автоматически означает ребро.
Недостатки метода в некоторой степени компенсируются его преимуществами.
Во-первых, это самый стабильный метод. Если входной полигон правильный, то и результат правильный для всех точек, за исключением точек на ребрах, но о них см.
выше.
Более того, метод позволяет частично бороться с неверными входными данными.
Многоугольник пересекает сам себя? Нет проблем, метод, скорее всего, правильно определит большинство точек.
Многоугольник не замкнут или вообще не многоугольник, а бессмысленный набор отрезков? Метод позволит правильно определить точки в большом количестве случаев.
В целом метод всем хорош, но он медленный и требует вычислений арккосинусов.
Как бы вы хотели закончить этот обзор? А то, что существует не один и даже не два метода решения задачи определения принадлежности точки многоугольнику.
Они служат разным целям, и некоторые больше подходят, когда важна скорость, другие — когда важно качество.
Ну и не забывайте, что у нас непредсказуемые входные данные и мы работаем с компьютером, арифметика с плавающей запятой подвержена ошибкам.
Если вам нужна скорость, а качество совершенно неважно, трассировка лучей может помочь.
В большинстве реальных приложений, вероятно, помогут метод ближайшей точки и обычный метод. Если первоочередной задачей является точность определения, когда входные данные неясны, то метод точечного индекса должен помочь.
Если у вас есть вопросы, спрашивайте.
Как человек, занимающийся геометрией и подобными проблемами, связанными с графикой, я буду рад помочь, чем смогу.
- С помощью скалярного произведения вычисляем угол, образованный векторами, начинающимися в проверяемой точке и заканчивающимися на концах ребра.

-
Эбботт, Чарльз Грили
19 Oct, 24 -
Гост По Удобству Использования
19 Oct, 24 -
Откуда Мы?
19 Oct, 24 -
Ежедневное Архивирование Веб-Проектов
19 Oct, 24 -
Вы Улыбались Сегодня?
19 Oct, 24


