Всем привет! Меня зовут Алексей Бурнаков.
Я специалист по данным в Align Technology. В этом материале я расскажу вам о подходах к выбору признаков, которые мы практикуем во время экспериментов по анализу данных.
В нашей компании статистики и инженеры по машинному обучению анализируют большие объемы клинической информации, связанной с лечением пациентов.
В двух словах, суть этой статьи можно свести к извлечению ценных крупиц знаний, содержащихся в небольшой части шумных и избыточных гигабайт данных, доступных нам.
Эта статья предназначена для статистиков, инженеров по машинному обучению и специалистов, заинтересованных в обнаружении зависимостей в наборах данных.
Также материал, представленный в статье, может быть интересен широкому кругу читателей, неравнодушных к интеллектуальному анализу данных.
В материале не будут затронуты вопросы проектирования признаков и, в частности, использования таких методов, как анализ главных компонент. 
Источник.
Установлено, что наборы с большим количеством входных переменных могут содержать избыточную информацию и приводить к переобучению моделей машинного обучения, если в модели не встроен регуляризатор.
Этап выбора информативных признаков ( ОИП здесь и далее) часто является необходимым этапом предварительной обработки данных в ходе эксперимента.
- В первой части статьи мы рассмотрим некоторые методы отбора признаков и рассмотрим теоретические аспекты этого процесса.
Этот раздел представляет собой скорее систематизацию наших взглядов.
- Во второй части статьи на примере искусственного набора данных мы поэкспериментируем с подбором информативных признаков и сравним результаты.
- В третьей части мы рассмотрим теорию и практику использования мер теории информации применительно к обсуждаемой проблеме.
Метод, представленный в этом разделе, является новым, но он по-прежнему требует многочисленных испытаний на различных наборах данных.
.
Кроме того, оговорка заключается в том, что ценность того или иного метода будет меняться при изменении других данных, что делает задачу в целом интеллектуально привлекательной.
В конце статьи будут подведены итоги экспериментов и сделана ссылка на полный R-код на Git. Выражаю благодарность всем людям, которые прочитали материал перед публикацией и сделали его лучше, в частности Владу Щербинину и Алексею Селезневу.
1) Методы и способы выделения информативных признаков.
Давайте посмотрим на общий подход к классификации методов интеллектуальной собственности, обратившись к Wiki:
Алгоритмы выбора информативных признаков могут быть представлены следующими группами: Обертки, Фильтры и Встроенные.Источник.(Эти термины я оставлю без точного перевода из-за неопределённости их звучания для русскоязычного сообщества – мой комментарий.
) Алгоритмы-оболочки создают подмножества путем поиска в пространстве возможных входных переменных и оценивают полученные подмножества входных данных путем обучения полной модели на доступных данных.
Алгоритмы-оболочки могут быть очень дорогими и могут привести к переобучению модели.
(Если не используется проверочный образец – мое примечание.
) Алгоритмы фильтрации аналогичны алгоритмам-оболочкам в том, что они также ищут подмножества входных данных, но вместо запуска полной модели важность подмножества для выходной переменной оценивается с использованием более простого алгоритма (фильтрации).
Алгоритмы, встроенные в машины, оценивают важность входных характеристик с помощью предварительно обученных эвристик.
Примеры.
Алгоритмом-оберткой OIP можно назвать комбинацию методов, включающую поиск подмножества входных переменных с последующим обучением, например, случайного леса, на выбранных данных и оценку его ошибки с помощью перекрестной проверки.
То есть на каждой итерации мы будем обучать целую машину (уже фактически готовую к дальнейшему использованию).
Алгоритм фильтрации OIP можно назвать перебором входных переменных, дополненным статистической проверкой связи между выбранными переменными и выходными данными.
Если наши входные и выходные данные категориальны, то можно провести критерий хи-квадрат на независимость между входом (или объединенным набором входов) и выходом с оценкой p-значения и, как следствие, двоичным выводом.
о значимости или незначительности выбранного набора признаков.
Другие примеры алгоритмов фильтрации включают:
- линейная корреляция входа и выхода;
- статистический тест на разницу средних значений в случае категориальных входных данных и непрерывного выходного сигнала;
- F-тест (дисперсионный анализ).
В этом случае значение p также позволяет сделать бинарный вывод о значимой разнице между коэффициентом и нулем.
Если мы масштабируем все входные данные модели, то весовые модули можно интерпретировать как показатели важности.
Вы также можете использовать R^2 модели — показатель того, как отклонение процесса объясняется смоделированными значениями.
Другой пример — функция оценки важности входных переменных, встроенная в случайный лес.
Кроме того, можно использовать весовые модули, соответствующие входам в искусственную нейронную сеть.
Этот список не исчерпывается.
На этом этапе важно понимать, что данное различие, по сути, указывает на различие функций приспособленности ИИП, то есть меры релевантности найденного подмножества входных признаков по отношению к решаемой задаче.
В дальнейшем мы вернемся к вопросу выбора фитнес-функции.
Теперь, когда мы немного разобрались с основными группами методов ИИП, предлагаю обратить внимание на то, какие методы используются для перебора подмножеств входных переменных.
Давайте еще раз посмотрим на страницу Wiki:
Подходы грубой силы включают в себя:Источник.
- Полный поиск
- Первый лучший кандидат
- Имитация отжига
- Генетический алгоритм
- Жадный поиск включения
- Жадный поиск исключений
- Оптимизация роя частиц
- Целенаправленное преследование проекций
- Скаттер-поиск
- Переменный поиск соседства
Я сознательно не стал переводить названия некоторых алгоритмов, так как не знаком с их русской интерпретацией.
Поиск подмножества предикторов является дискретной задачей, так как на выходе мы получаем вектор целых чисел, обозначающих индексы входов, вида: входы: 1 2 3 4 5 6… 1000 выбор: 0 0 1 1 1 0… 1 Мы вернемся к этой особенности позже и проиллюстрируем, к чему она ведет на практике.
Результат всего эксперимента во многом зависит от того, как настроен поиск подмножества входных признаков.
Чтобы интуитивно понять основную разницу этих подходов, предлагаю читателю разделить их на две группы: жадные и нежадные.
Жадные алгоритмы поиска.
Их часто используют, поскольку они быстрые и дают хорошие результаты во многих задачах.
Жадность алгоритма заключается в том, что если один из кандидатов на включение в итоговое подмножество выбран (или исключен), то в дальнейшем он остается в нем (в случае жадного включения) или отсутствует навсегда (в случае жадного включения).
случай жадного исключения).
Таким образом, если кандидат А был выбран на ранних итерациях, на последующих итерациях подмножество всегда будет включать его и других кандидатов, которые вместе с А демонстрируют улучшение показателя важности подмножества для выходной переменной.
Обратная ситуация для исключения: если кандидат А был удален, потому что метрика важности меньше всего пострадала или улучшилась после его исключения, исследователь не получит информацию о метрике важности, в которой подмножество содержит А и других кандидатов, исключенных позже.
Если провести параллель с поиском максимума (минимума) в многомерном пространстве, то жадный алгоритм застрянет в локальном минимуме, если он есть, или быстро найдет оптимальное решение, если есть единственный минимум, и оно является глобальным.
С другой стороны, перебор всех жадных опций происходит относительно быстро и позволяет нам учесть некоторые взаимодействия между входными данными.
Примеры жадных алгоритмов: жадное включение (выбор вперед; шаг вперед) и жадное исключение (исключение назад; шаг назад).
Список этим не ограничивается.
Нежадные алгоритмы поиска.
Принцип работы нежадных алгоритмов предполагает возможность отбрасывать полностью или частично сформированные подмножества признаков, комбинации подмножеств друг с другом, а также вносить случайные изменения в подмножества во избежание локального минимума.
Если провести аналогию с поиском максимального (минимального) значения фитнес-функции в многомерном пространстве, то нежадные алгоритмы рассматривают гораздо больше соседних точек и даже могут совершать большие скачки в случайные области.
Вы можете графически представить работу этих типов алгоритмов.
Сначала жадное включение: 
Теперь нежадный - стохастический - поиск: 
В обоих случаях вам необходимо выбрать одну лучшую комбинацию двух входных данных, индексы которых отложены по осям графика.
Жадный алгоритм начинается с выбора единственного лучшего входного сигнала путем горизонтального вращения индексов.
А затем добавляет второй вход к выбранному входу, чтобы их общая релевантность была максимальной.
Но оказывается, что из всех возможных комбинаций он выполняет только 1/37 из них.
При добавлении еще одного измерения количество пройденных ячеек станет еще меньше: примерно 1/37^2. В этом случае возможна практическая ситуация, когда наилучшая комбинация не та, которую находит жадный алгоритм.
Это может произойти, если каждый из двух входов по отдельности не показывает лучшую релевантность задаче (и они не выбираются на первом этапе), но их взаимодействие максимизирует метрику релевантности.
Нежадный алгоритм ищет гораздо дольше:
(О) = 2^nи проверяет больше возможных комбинаций входов.
Но у него есть шанс найти, возможно, еще лучший подмножество входных данных благодаря тщательному поиску по всем вариантам проблемы одновременно.
Существуют алгоритмы поиска, выходящие за рамки установленной дихотомии жадный/нежадный.
Примером такого отдельного поиска может быть поочередное перебор входных данных и оценка их индивидуальной важности для выходной переменной.
Кстати, именно здесь начинается первая волна в алгоритме жадного включения переменных.
Но какая польза от такого рода грубой силы, кроме того, что он очень быстрый? Каждая входная переменная начинает существовать «в вакууме», то есть без учета влияния других входов на взаимосвязь между выбранными входом и выходом.
При этом после завершения работы алгоритма результирующий список входов с указанием их индивидуальной важности для выхода предоставляет информацию только об индивидуальной значимости каждого предиктора.
При объединении определенного количества наиболее важных предикторов по такому списку можно получить ряд проблем:
- избыточность (в случае корреляции предикторов друг с другом);
- недостаточная информация из-за неучёта взаимодействия предикторов на этапе выбора;
- размытие границы, выше которой следует брать предикторы.
Основной вопрос в задаче ОИП формулируется как оптимальное сочетание метода поиска подмножеств и функции приспособленности.
Давайте подробнее рассмотрим это утверждение.
Нашу задачу ОИП можно описать двумя гипотезами: а) поверхность ошибки является простой или сложной; б) данные содержат простые или сложные зависимости.
В зависимости от ответов на эти вопросы следует выбрать конкретное сочетание метода поиска и метода определения релевантности выбранных признаков.
Поверхность ошибки.
Пример простой поверхности: 
Источник.
Здесь мы выбираем комбинацию двух входов, определяем их соответствие выходу и двигаемся вниз по гладкой поверхности в направлении градиента, почти наверняка достигая оптимальной точки.
Пример сложной поверхности: 
Источник.
В этом случае при решении одной и той же задачи мы встречаем множество локальных минимумов, из которых жадный алгоритм не может выбраться.
В то же время алгоритм со стохастическим поиском имеет повышенные шансы найти более точное решение.
Ранее мы упоминали, что поиск подмножества предикторов — дискретная задача.
Если зависимость выхода от входов включает взаимодействия, то при перемещении из одной точки пространства в соседнюю можно наблюдать резкие скачки значения фитнес-функции.
Поверхность ошибок в нашем случае зачастую не гладкая и не дифференцируемая: 
Это пример поиска подмножества двух входных данных и соответствующего значения функции релевантности подмножества выходной переменной.
Видно, что поверхность далеко не гладкая, с пиками, а также включает изрезанные плато примерно таких же величин.
Кошмар для жадных методов градиентного спуска.
Зависимости.
По мере увеличения числа измерений проблемы увеличивается теоретическая вероятность того, что зависимость выходной переменной имеет очень сложную структуру и включает в себя множество входных данных.
При этом зависимость может быть как линейной, так и нелинейной.
Если зависимость предполагает взаимодействие предикторов и нелинейную форму, то найти ее можно только с учетом обоих этих моментов, используя, например, обучение случайного леса или нейронную сеть.
Если зависимость простая, линейная и включает лишь небольшую часть всех предикторов, подход к ее нахождению - и, как следствие, к ИИП - может быть сведен к поочередному включению в модель линейной регрессии одного или нескольких входов с оценка качества модели.
Пример простой зависимости: 
В этом случае зависимость значения по выходной оси от значений input1 и input2 описывается плоскостью в пространстве:
выход = вход1*10 + вход2*10Модель такой зависимости очень проста и может быть аппроксимирована линейной регрессией.
Пример сложной зависимости: 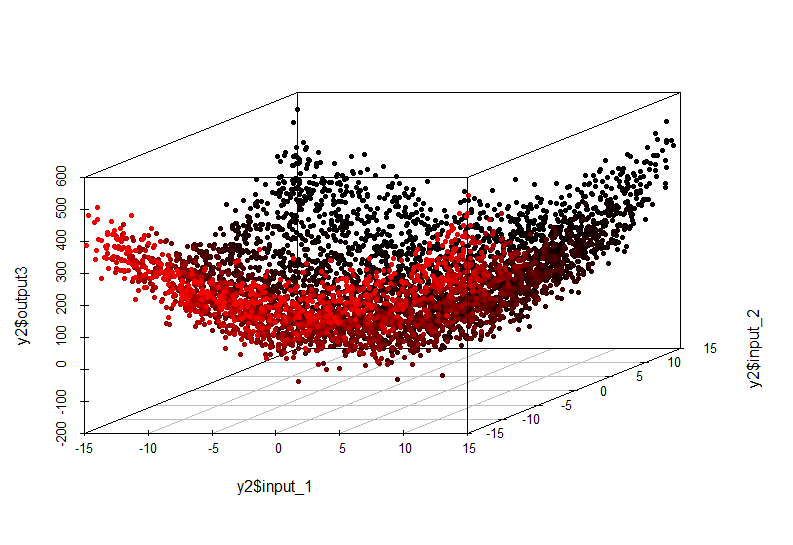
Эту нелинейную зависимость уже невозможно выявить путем построения линейной модели.
Его внешний вид следующий:
выход = вход1^2 + вход2^2Также необходимо учитывать масштабность проблемы.
Если количество входных переменных велико, поиск оптимального подмножества с помощью стохастических (нежадных) методов может оказаться очень дорогостоящим из-за того, что общее количество всех возможных подмножеств определяется соотношением
м = 2^n, где n — количество всех входных объектов.Соответственно, поиск минимума в таком многообразии может быть очень долгим.
С другой стороны, использование жадного поиска позволит сделать первое приближение за разумное время, даже если это локальный минимум и исследователь о нем знает. При отсутствии предметных знаний об изучаемом явлении невозможно заранее сказать, насколько сложной будет зависимость входных переменных и выхода и какое количество входов будет оптимальным для нахождения приближенного или точного решения задачи выбор оптимального подмножества входов.
Также трудно предсказать, будет ли поверхность ошибок в OIP гладкой и простой или сложной и неровной.
Мы также всегда ограничены в ресурсах и должны принимать наиболее оптимальные решения.
Следующая таблица может быть использована в качестве небольшой помощи при разработке подхода к защите прав интеллектуальной собственности:
Таким образом, у нас всегда есть возможность рассмотреть несколько комбинаций методов поиска входного подмножества и функций соответствия релевантности.
Самая дорогая и, вероятно, самая эффективная комбинация — жадный поиск и фитнес-функция-обёртка.
Позволяет избежать локального минимума, обеспечивая при этом наиболее точную меру релевантности выбранных входных данных, поскольку на каждой итерации имеется обученная модель (и ее точность при проверке).
Наименее затратный, но не всегда наименее эффективный подход — это жадный поиск в сочетании с функцией фильтра, которая может представлять собой статистический критерий, коэффициент корреляции или количество взаимной информации.
Кроме того, встроенные методы позволяют сразу после обучения модели отфильтровывать ряд ненужных с точки зрения алгоритма входных данных без существенной потери точности моделирования.
Хорошей практикой является несколько раз попытаться решить задачу разными способами и выбрать лучший.
Вообще говоря, выбор информативных признаков – это выбор наилучшего сочетания метода поиска в многомерном пространстве и наиболее оптимальной фитнес-функции релевантности выбранного подмножества по отношению к выходной переменной.
2) эксперименты по выделению информативных признаков на синтетических данных.
Наш тестовый набор данных (Стэнфордский кролик):
Я просто обожаю кроликов.
Мы рассмотрим зависимость высоты точки (ось Z) от широты и долготы.
В этом случае я добавляю в набор 10 шумовых переменных с распределением, примерно соответствующим смеси двух информативных входов (X и Y), но никак не связанных с переменной Z. Давайте посмотрим на гистограммы плотности распределения переменных X, Y, Z и одной из шумовых переменных.
Видно, что распределения имеют произвольные параметры.
В этом случае все шумовые переменные распределяются так, что имеют небольшой пик в определенном диапазоне значений.
Далее набор данных будет случайным образом разделен на две части: обучение и проверка.
Подготовка данных.
Код
Теги: #выбор функций #выбор информативных функций #статистика #Машинное обучение #теория информации #регрессия #нейронные сети #Случайный лес #деревья с градиентным усилением #Интеллектуальный анализ данных #rlibrary(onion) data(bunny) #XYZ point plot open3d() points3d(bunny, col=8, size=0.1) bunny_dat <- as.data.frame(bunny) inputs <- append(as.numeric(bunny_dat$x),

-
Очистка Реестра Компьютера
19 Oct, 24 -
Офис В России
19 Oct, 24 -
Html5 Будет Готов К 2014 Году, Что Дальше?
19 Oct, 24



