Добрый день Как и было обещано в его первая статья , хочу познакомить вас с одним из методов решения системы диофантовых уравнений.
Цель статьи – познакомить других читателей с этой техникой и донести ее в более-менее понятной форме.
Рассмотрим систему двух диофантовых уравнений 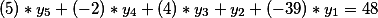
И 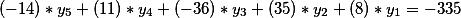
Найдем все возможные решения первого уравнения.
Как, спросите вы? Вероятно, существуют разные методы, но в одной из следующих статей я поделюсь, как бы я решил подобную проблему.
Теперь предположим, что общее решение имеет вид 
Как мне проверить, что я не вру? Достаточно вспомнить матричное исчисление и умножим вектор значений нашего первого диофантова уравнения (без фиктивного члена) на матрицу всех коэффициентов .
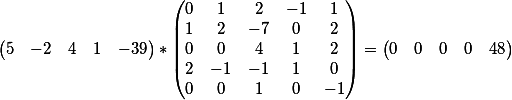
В результате мы получили значение свободного срока, а значит расчеты верны.
Следующим шагом будет замена нашего общего решения 
во второе уравнение 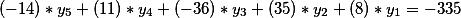
Порядок тот же: вектор коэффициентов второго уравнения умножаем на общее решение первого.
мы получаем этот результат 
то есть мы получили уравнение вида 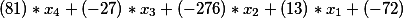
В правой части второго диофантова уравнения как был свободный член, равный -335, так и остался, то есть наше окончательное решение на этом этапе имеет вид 
Или, переместив свободные члены в правую часть, получим 
Итак, мы получили еще одно диофантово уравнение.
Найдем ее общее решение и проверим его на истинность.
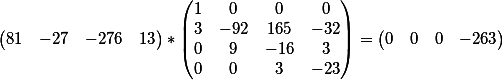
то есть общее решение имеет вид 
Теперь делаем обратное преобразование (пусть оно так и называется).
То есть в систему 
Вместо неизвестного х подставляем то, что получили на последнем этапе 
В матричном исчислении эта проблема решается путем умножения одной матрицы на другую.
А вот с первой матрицей нужно проделать определенную процедуру: удалить (временно) последний столбец со свободными членами, так как этот параметр не участвует в умножении и будет использоваться в дальнейшем.
Результат умножение двух матриц генерирует 
матрица 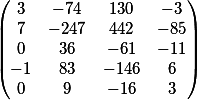
Последний столбец — свободные участники этой системы.
Примем во внимание столбец, который был временно удален перед умножением, и сложим их.
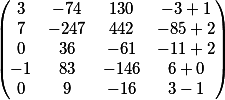
наш окончательный ответ в матричной форме 
Проверим? Векторное произведение коэффициентов первого уравнения и матрицы 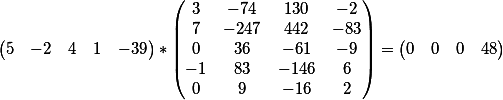
и векторное произведение коэффициентов второго уравнения и матрицы 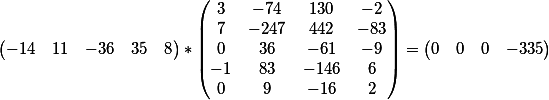
Как видим, результат совпадает со свободным членом каждого из уравнений.
Таким образом, общее решение имеет вид 
где m,p,q может принимать любые целые значения Более сложные линейные диофантовые уравнения можно решить таким простым способом.
Следуя этому алгоритму калькулятор создан Однако этот калькулятор очень не любит, когда вместо значений в коэффициентах первого уравнения исходной системы стоят нули.
Но это проблема моей конкретной реализации этого алгоритма.
В следующей теме я расскажу вам, как создавать диофантовы уравнения, используя общую матрицу решений.
Задача в целом тривиальная и делается за одно действие, но вдруг кто-то не знает. Буду благодарен за комментарии, отзывы и предложения.
Теги: #математика #программирование #Матрица #Система #диофантовые #уравнения
-
Подготовка Образа Виртуальной Машины Windows
19 Oct, 24 -
«Яндекс Для Бизнеса» В Харькове
19 Oct, 24 -
Чистый Код С Помощью Google Guava
19 Oct, 24


