Введение Эта статья не относится к сериалу «Магия тензорной алгебры».
, но оживлённый публикациями из него.
Неосторожно переходя по ссылкам в поисковике, я наткнулся обсуждение одной из ваших статей посвященный эффекту Джанибекова, и обратил внимание на справедливое замечание о том, что исследование устойчивости гайки Джанибекова в первом приближении не дает однозначного ответа на вопрос, при каких параметрах движение будет устойчивым.
Это так, поскольку корни характеристического многочлена при вращении вокруг оси с наименьшим и наибольшим моментом инерции чисто мнимые, их действительная часть равна нулю.
В таких условиях невозможно ответить на вопрос, будет ли движение устойчивым, без проведения дополнительных исследований.
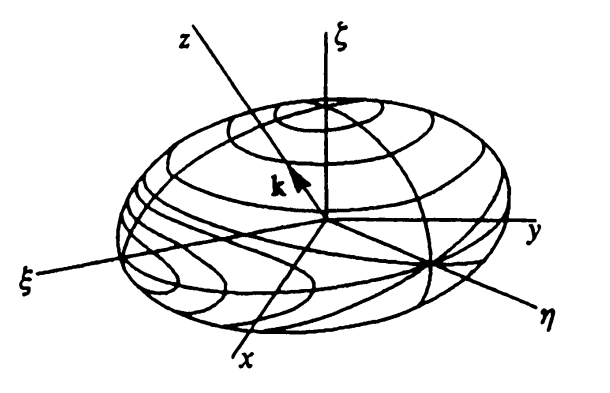
Интерпретация МакКалла, вероятно, является самым простым объяснением эффекта Джанибекова.
Такое исследование можно провести методом функций Ляпунова ( второй или прямой метод Ляпунова).
И чтобы окончательно закрыть вопрос с гайкой Джанибекова, я решил написать эту заметку.
1.Дифференциальные уравнения возмущенного движения.
Снова.
Пусть имеется система, в общем случае, нелинейных дифференциальных уравнений движения некоторой механической системы
Где
— вектор-столбец переменных состояния системы;
является нелинейной векторной функцией.
Системное решение (1)
дает так называемый беспрепятственное движение .
По сути, это нормальный, установившийся режим движения системы под действием приложенных к ней сил.
Определим некоторое возмущение, определяемое вектором
отклонения от невозмущенного движения, т.
Подставив (3) в (1), получим
Вычтите (1) из (4)
или
Где
, а полученное уравнение называется уравнением возмущенное движение , тривиальное решение которого
соответствует невозмущенному движению системы.
В нашем случае ограничимся рассмотрением автономной системы, где правая часть явно не зависит от времени.
2. Хитрая функция В ( Икс ) — кандидат в функцию Ляпунова
Рассмотрим некоторую скалярную функцию
определено в некоторой окрестности начала координат такой, что
Где
- некоторое довольно небольшое положительное число.
Функция (6) называется определенный знак , если в области (7) она принимает значения только одного знака (только положительного или только отрицательного) и равна нулю только в начале координат (в точке
)
Функция (6) называется постоянный знак , если в области (7) принимает значения только одного определенного знака, но может обращаться в нуль даже при
.
Вычислим полную производную функции (6) по времени.
Потому что
, по определению полной производной получаем
что с учетом уравнения (5) эквивалентно соотношению
Функцией (8) называется полная производная функции (6) по времени, составленная на основании уравнения (5).
3. Теоремы Ляпунова об устойчивости.
Два приведенных выше абзаца написаны сухим математическим языком определений, и иначе, наверное, и быть не может. Добавим еще немного формальной математики, сформулировав
Теорема устойчивости Ляпунова
Если для системы уравнений (5) существует знакоопределяемая функцияПод точкой покоя системы (5) здесь понимается ее тривиальное решение, соответствующее невозмущенному движению рассматриваемой механической системы.
(функция Ляпунова), полная производная по времени, составленная в силу системы (5), является знакомо-постоянной функцией, знак противоположный В , или тождественно равна нулю, то точка покоя системы (5)
стабильный
Грубо говоря, согласно сформулированной теореме следует выбрать функцию
, удовлетворяющий свойствам, указанным в условиях теоремы.
Если она удовлетворяет этим свойствам, то она называется функцией Ляпунова, и если такая функция (хотя бы одна!) существует, то установившееся состояние движения рассматриваемой механической системы будет устойчивым.
Однако эта теорема не касается асимптотический устойчивость, то есть характер движения системы, при котором ее возмущенное движение будет стремиться к исходному устойчивому состоянию.
Стабильность здесь также означает движение, при котором система будет колебаться вблизи исходного устойчивого состояния, но никогда не вернется к нему.
Условие асимптотической устойчивости будет более жестким.
Теорема Ляпунова об асимптотической устойчивости
Если для системы уравнений (5) существует знакоопределяемая функцияАсимптотически устойчивая система после возмущения будет стремиться вернуться к установившемуся состоянию движения, то есть решение системы (5) будет сходиться к началу координат
(функция Ляпунова), полная производная которой по времени, составленная в силу системы (5), представляет собой знакоопределяемую функцию противоположного знака В , то точка покоя системы (5)
асимптотически устойчивый
.
Эти теоремы дают более общий способ исследования устойчивости линейных и нелинейных механических систем, чем исследование первого приближения.
Другой вопрос – как найти функцию Ляпунова, удовлетворяющую уравнению (5) и требованиям теорем.
Математика пока не знает однозначного ответа на этот вопрос.
Данной проблеме целиком посвящен ряд работ, например книга Е.
А.
Барабашина «Функции Ляпунова» .
Для большинства линейных систем функции Ляпунова можно искать в виде квадратичных форм, например, для системы третьего порядка эта функция может иметь такой вид
эта функция заведомо положительна и находится в сколь угодно большой окрестности точки покоя системы.
Или такая функция
будет иметь постоянный знак, положительный, потому что
может быть равна нулю, как и в точке покоя системы
, и в точке, удовлетворяющей условию
.
В случае консервативных механических систем функцией Ляпунова может быть полная механическая энергия системы, которая при отсутствии диссипации является константой (знак константы), а также производная по времени, равная нулю, - это константа.
А эта функция следует из системы уравнений движения, поскольку является одним из ее интегралов.
В случае с гайкой Джанибекова я взял идею из книги как очень изящное решение А.
П.
Маркеева «Теоретическая механика» .
Это решение было мной немного переработано и расширено в контексте ранее написанных статей.
4. Интегралы движения гайки Джанибекова.
Первые два интеграла движения получим на основе к системе уравнений, заданной в тензорном цикле .
Мы будем оперировать тензорными отношениями, чтобы не потерять хватку.
Итак, уравнение вращения гайки вокруг центра масс имеет вид
Перейдем в этом уравнении к вектору МКД
Умножим уравнение (10) скалярно на удвоенный вектор МКД
Легко видеть, что во втором слагаемом (11) свертка
, а в первом - производная квадрата модуля МКД.
Преобразуем уравнение (11) и проинтегрируем его
или
Выражение (12) является первым интегралом движения, выражающим постоянство модуля МКД рассматриваемой нами гайки.
Чтобы получить еще один первый интеграл движения, умножьте (9) скалярно на вектор угловой скорости
после чего вдруг обнаруживаем свертку во втором члене
равен нулю, что дает уравнение
Давайте вспомним, что-то подобное мы уже видели раньше .
Ведь кинетическая энергия тела при его вращении относительно центра масс равна
и если мы продифференцируем его по времени, что мы получим
согласно этому мы можем переписать уравнение (13) и проинтегрировать его
Учитывая, что умножение константы на два не меняет ее «постоянства», мы наконец можем записать первый интеграл в компонентном виде (с учетом декартова базиса!)
Выражение (14) выражает постоянство кинетической энергии вращения гайки вокруг центра масс.
Осталось в выражениях (12) и (14) перейти к безразмерным моментам инерции
Полученные уравнения являются первыми интегралами движения, которые мы используем для построения функции Ляпунова
4. Построение функции Ляпунова по интегралам движения
Метод построения функции Ляпунова из уравнений вида (15) называется Интегральный связочный метод Четаева и говорит, что обозначенную функцию можно искать в виде связки интегралов движения вида
Где
— первые интегралы уравнений возмущенного движения;
И
– неопределенные константы, подбором которых можно сделать функцию (16) заведомо положительной, удовлетворяющей теореме Ляпунова об устойчивости.
Невозмущенное вращение гайки происходит вокруг оси.
с постоянной угловой скоростью
.
Возмутим это движение, придав угловой скорости небольшое приращение
, и перепишем выражения (15)
или
При установившемся вращении гайки с постоянной угловой скоростью постоянная
можно вычесть из обеих частей полученных уравнений, получив в их левой части функции
Функция Ляпунова будет иметь вид
Из уравнений (15) видно, что
, а значит, об асимптотической устойчивости не может быть и речи.
Но, исходя из теоремы Ляпунова, необходимо убедиться, что функция (18) заведомо положительна.
Из выражений (18) и (17) видно, что его значения положительны при любых
,
И
.
Теперь покажем, что (18) обращается в нуль только в точке покоя системы
.
Выражение (18) равно нулю только в случае
Из первого уравнения системы (19) вычитаем второе
Если
(момент инерции, вокруг которого вращается гайка величайший ), или
(момент инерции, вокруг которого вращается гайка наименее ), то равенство (20) будет справедливо только в том случае, когда
.
Учтем этот факт и сложим уравнения (19)
Уравнение (21) справедливо для
и в
.
Но поскольку мы верим
, функция (18) будет равна нулю исключительно в точке покоя системы
.
Таким образом, вращение гайки вокруг оси с наименьшим и наибольшим моментом инерции будет устойчивым по Ляпунову.
Однако спешу отметить, что когда
, или
, то есть когда момент инерции относительно оси, вокруг которой происходит вращение, имеет промежуточное значение между максимальным и минимальным, функцию (18) уже нельзя назвать положительно определенной, в связи с тем, что слагаемые в (20 ) будут иметь разные знаки.
Но вовсе нельзя сказать, что движение будет неустойчивым.
Особенность теорем Ляпунова об устойчивости состоит в том, что они декларируют условие устойчивости, но не декларируют обратное.
Неустойчивость движения придется доказывать отдельно.
5. Нестабильность вращения гайки Джанибекова.
Давайте сформулируем определение
Областьи теорема
позвоним в любой район округа
, где для некоторой функции
условие выполнено
, и на границе области
и остальная точка системы принадлежит этой границе.
Теорема Четаева о неустойчивости
Если дифференциальные уравнения возмущенного движения (5) таковы, что существует функцияФункция
, такая, что в сколь угодно малой окрестности
есть территория
, и во всех точках этой области производная
в силу уравнений (5) принимает положительные значения, то невозмущенное движение неустойчиво.
которое упоминается в теореме, называется Функция Четаева .
Теперь рассмотрим еще раз нашу гайку, уравнения вращения которой выглядят так (с учетом работы в декартовых координатах, связанных с телом, и введенных нами безразмерных моментов инерции)
Учитывая, что первоначально вращение происходит с постоянной угловой скоростью
вокруг оси
, построим уравнения возмущенного движения.
Мы будем считать, что
- этого всегда можно добиться, выбрав оси собственной системы координат.
Построим функцию Четаева
Теги: #эффект Джанибекова #эффект Джанибекова #гайка Джанибекова #стабильность #второй метод Ляпунова #метод функции Ляпунова #теорема Четаева #функция Ляпунова #математика

-
Функция И Функциональный Объект
19 Oct, 24 -
Эффективный Перевод
19 Oct, 24


