В комментариях к предыдущей статье " О чем молчит диаграмма Ганта или почему проекты всегда опаздывают » предоставлены ссылки на видеоролики и слайдкасты с описанием других причин, вызывающих ошибки при использовании диаграмм Ганта.
Наибольшее обсуждение и непонимание вызвало спрямление сроков из-за асимметрии распределения сроков решения задачи.
Ниже под катом приведен пример влияния этого очень асимметричного распределения на дату завершения проекта.
Прежде чем начать, напомню, что в приведенных примерах значения времени, используемые для решения задачи, взяты из некоторого предыдущего опыта и являются объективными.
Приведенные примеры призваны продемонстрировать, что при построении диаграммы Ганта, опираясь только на математическое ожидание времени выполнения отдельной задачи, мы попадем в тупик.
Рассмотрим пример, в котором наиболее вероятное время решения проблемы составляет 3 часа.
Совершенно ясно, что существует некоторое время, раньше которого мы не сможем решить проблему.
Нам нужно прочитать задачу, посмотреть связанные задачи, обсудить те или иные вопросы с аналитиком или архитектором, открыть IDE, загрузить проект, внести изменения в код, собрать, запустить, проверить, что все работает как положено и т. д. Допустим, мы не можем решить проблему менее чем за 30 минут. Но, с другой стороны, если возникнут проблемы с компьютером (маловероятно, но все же), если обнаружен связанный с этим баг и если на месте не окажется сотрудника, с которым нужно согласовать решение проблемы, срок может увеличиться до 6, а то и до 9 часов.
В результате получаем плотность распределения вероятностей вида (по оси абсцисс — время решения задачи): 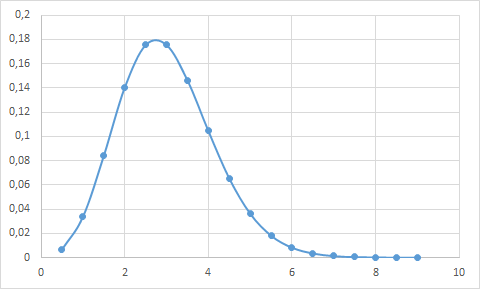
И это уже не нормальное распределение.
Для этой статьи я взял гамма-распределение , есть и другие, например, Распределение Максвелла , бета-распределение и т. д. Отлично, как я уже сказал, ожидаемое время решения проблемы — три часа.
Диаграмма Ганта для пяти последовательно выполняемых задач будет выглядеть так: 
Теперь вернемся к гамма-распределению и проведем расчет или (как это сделал я, я очень люблю программирование) моделирование вероятности прохождения всех этапов в заданный час.
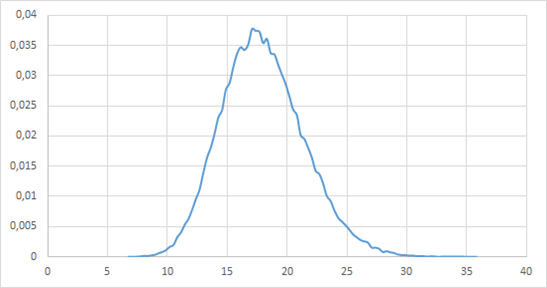
Первая новость - хорошая новость, плотность распределения вероятностей приняла вид нормального распределения, а все остальное.
Чтобы понять остальное, построим вероятность завершения к заданному часу: 
Вероятность завершения к запланированным 15:00 составляет всего 20%.
Для достижения вероятности 90% время завершения необходимо сдвинуть на 7 часов (что составляет 50% от исходного времени).
И тогда в случае с оставшимися 10% мы не уложимся в срок и с вероятностью 5% выполним эти пять задач за 9 часов.
Еще одна печальная новость заключается в том, что даже использование популярной в последнее время методики трехоценки ситуацию не сильно улучшает. Если вы не помните, основная идея метода трех оценок заключается в том, что вы берете пессимистический прогноз, оптимистический прогноз и математическое ожидание.
В этом случае дата завершения задачи определяется по формуле: 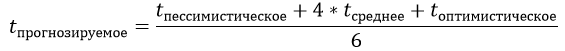
Для нашего случая, если за оптимистичный прогноз принять вероятность 30% для одной задачи, за пессимистичный 95% и за наиболее ожидаемый 50%, то на основе графика вероятности выполнить одну задачу к заданному часу : 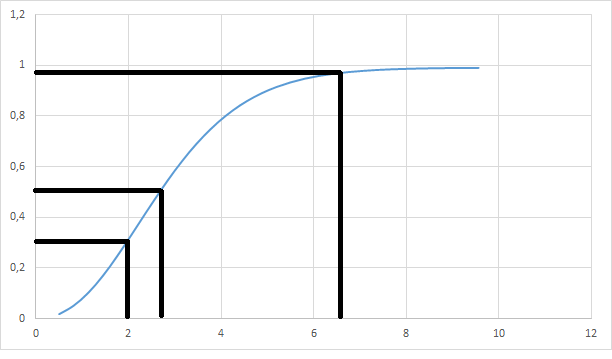
Мы получаем это: 
Умножаем 3,7 часа на 5 стадий и получаем 18,5 часов.
Это уже гораздо лучше, мы уложимся в этот срок с вероятностью 75%.
А в четверти случаев мы продолжим срывать сроки.
Ссылки на материалы из комментариев к предыдущей статье: 1. Условия сжигания Пуассона 2. Человеческое и математическое выравнивание сроков P.s. За прочтение и советы по статье огромная благодарность Андрею Потапову, CrazyViper И Картмендум (последнему за упрек в моем незнании теории вероятностей).
Теги: #Диаграмма Ганта #Распределение Гаусса #Управление проектами #гамма-распределение #Управление проектами

-
Жесткий Диск
19 Oct, 24 -
От Аутсорсинга К Разработке (Часть 2)
19 Oct, 24 -
Вы Понимаете, Что Такое Облачные Вычисления?
19 Oct, 24 -
Многопоточный Сервер Socks 4 На Qt
19 Oct, 24


