Вопреки правилам пользования метро, желая сэкономить время, каждый из нас хотя бы раз в жизни спускался по эскалатору.
На первый взгляд кажется, что это абсолютно логично и правильно: если хочешь уйти быстрее, постарайся оказаться на платформе как можно раньше.
Однако практически сразу на ум приходит следующий сценарий: вы летите стремглав вниз по эскалатору, спускаетесь на платформу, и двери вагона закрываются прямо у вас перед носом.
Пока вы ждете следующего поезда, люди, вошедшие на эскалатор одновременно с вами, успевают спокойно спуститься вниз, стоя на месте, и сесть на следующий поезд. В этом случае выигрыша нет. Так насколько же рационально спускаться по эскалатору и стоит ли вообще это делать? Спешу вас обрадовать – ответ найден! Ниже приведено математическое обоснование нецелесообразности (да, НЕ) спускаться по эскалатору в метро.
Постановка проблемы
Прежде чем перейти к математическим рассуждениям, стоит упомянуть, что я, естественно, далеко не первый, кто задумался над этим вопросом.В Интернете можно найти достаточное количество статей и даже сюжетов федеральных каналов на эту тему.
Однако каждый раз суть такого рода эксперимента заключается в простом спуске по эскалатору с последующим сравнением полученного времени со временем стоящего на эскалаторе человека.
Чуть лучше, если авторы попытаются оценить эффективность скоростного спуска.
Еще лучше, если они еще и статистику представят. Кстати, за приведенную ниже статистику скажу отдельное спасибо.
Ввиду неясности этих экспериментов и отсутствия практических выводов я задумал и впоследствии осуществил анализ происходящего процесса.
И так, сформулируем условия задачи и обозначим ограничения:
- В (мысленном) эксперименте два человека одновременно приближаются к эскалатору в случайное время и понятия не имеют, где находится поезд.
- Один из этих людей стоит на эскалаторе и теряет время, спускаясь вниз.
, равный времени движения эскалатора. - Второй ускоряется вниз по эскалатору, увеличивая его скорость на
раз, тем самым сократив время спуска на такую же величину:
. - Ээффективный Ускоренным спуском считается такой, что человек, стоящий на эскалаторе, не успевает сесть в поезд, в который успевает сесть человек, бегущий по эскалатору.
- Обозначим через
– вероятность эффективного снижения.Тогда, согласно равновесию Нэша, человек готов пойти на риск и спуститься по эскалатору только в том случае, если вероятность эффективного спуска больше или равна вероятности неэффективного спуска или остановки на месте, то есть 0,5. .
Если вероятность эффективного спуска больше или равна 0,5, будем называть решение о спуске по эскалатору целесообразный .
Если меньше 0,5 – неприличный .
- Давайте пренебрегаем тем, что в реальной жизни, как правило, после схода с эскалатора до вагона необходимо пройти еще некоторое расстояние или подождать, пока люди выйдут из вагона, поезда ходят с переменными интервалами и некоторое время стоят на месте.
до открытия и после закрытия дверей, то есть будем считать, что если в момент схода с эскалатора поезд стоит на станции, то его двери открыты и участник эксперимента мгновенно оказывается в вагоне, Поезд сам открывает (закрывает) двери и прибывает (уходит) на станцию (со станции) мгновенно и сразу.
Ход решения
Изобразим ось времени (рис.1).
Вся ось будет представлять последовательные интервалы между поездами.
Здесь и далее будет рассматриваться только один интервал.
Разделите изображенный интервал на 4 равных отрезка.
Точка 0 на этой оси соответствует моменту отправления поезда со станции.
Точка 3 соответствует приходу поезда и открытию дверей.
Пункт 4 – закрытие дверей и отправление поезда.
Таким образом, для удобства графического представления и расчетов отсчитываем интервал между поездами между моментами отправления поездов со станции.
Первые 3 отрезка — это время, в течение которого пассажиры вынуждены ждать прибывающий поезд. Четвертый сегмент — это момент остановки поезда, когда пассажиры могут в него сесть.
Предположим также, что время
(время спуска по эскалатору) равно двум отрезкам.
Коэффициент
равно 2, то есть время спуска при беге в 2 раза меньше и равно одному отрезку.
Теперь, чтобы определить вероятность
, давайте выясним, через какой промежуток времени принятие решения о спуске бегом приведет к тому, что спуск окажется эффективным.
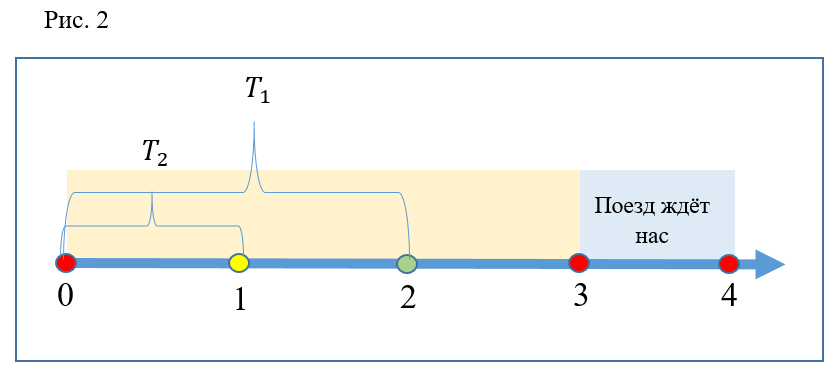
Например, если наши участники подойдут к эскалатору в момент 0, то первый из них окажется на платформе в момент времени.
(рис.
2), а второй ранее, на данный момент
.
Но, как видно из рисунка, ни в один из этих моментов времени поезда на станции нет, а значит, сбег был неэффективен.
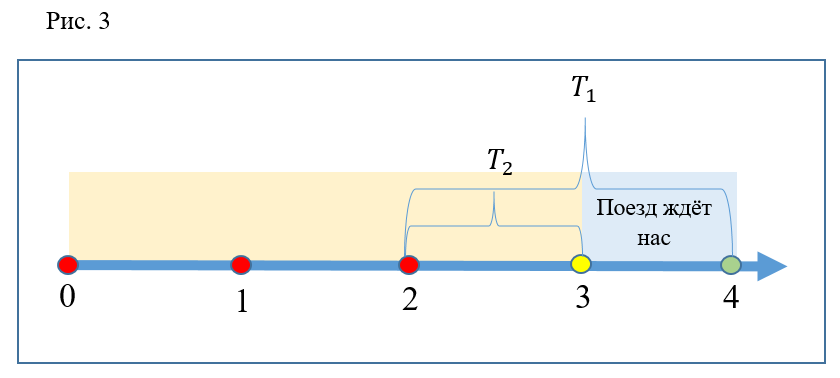
Рассмотрим другой случай (рис.
3): участники эксперимента подходят к эскалатору в момент 2. Как и в предыдущем случае, первый из них окажется на платформе в момент времени
, а второй раньше, в данный момент
.
Но очевидно, что оба раза на станции стоит поезд. Это значит, что оба успеют сесть в один и тот же поезд, поэтому сбегать было так же неэффективно.
Далее нетрудно понять, что в любой момент времени на отрезке от 2 до 3 бег вниз эффективен, так как бегущий всегда успевает сесть в поезд, а не бегущий - нет. Если мы выберем моменты времени между 3 и 4, то оба участника опаздывают на поезд и вынуждены вместе ждать следующего, то есть бег снова становится неэффективным.
Получается, что из 4-х условных временных интервалов сбегать эффективно только в том случае, если участники подходят к эскалатору в промежутке между 2 и 3-м моментами времени (рис.
4).
Вероятность попадания равна 1/4. Следовательно, при данных условиях задачи принятие решения о сбегании нецелесообразно, так как второй участник с большей вероятностью (с вероятностью 3/4) побежит зря и будет вынужден ждать поезда вместе с первым.
, который прибыл позже.

Следующие комментарии абсолютно справедливы:
- Интервалы между поездами могут как уменьшаться, так и увеличиваться.
Время парковки может увеличиться, а время ожидания уменьшиться (с одинаковым интервалом) и наоборот.
- Скорость эскалатора вниз постоянна, но время спуска может варьироваться, поскольку станции могут быть более или менее глубокими.
- Второй участник вполне может бежать не в 2, а в 3 и даже в 4 раза быстрее эскалатора.
Для этого изобразим еще один случай (рис.
5).
Оставим все исходные данные неизменными, кроме одного: коэффициента
увеличиться до 4. То есть второй участник окажется внизу в 4 раза быстрее, чем первый.
Для удобства изображения разделим наш интервал на 8 равных частей.
Таким образом, время спуска по эскалатору теперь составляет 4 сегмента, остановка поезда — два, время ожидания — 6, время движения — один.
Нетрудно узнать, что теперь длина «эффективного» периода времени (от 4 до 7 моментов времени) равна 3. То есть вероятность
равен 3/8. Это уже больше, чем в первом случае, но мы не делали эти изменения для оценки вероятности.
Исходя из рисунков 4 и 5, очевидно, что длина «эффективного» отрезка равна
.
Разделите его на длину интервала и получите вероятность
, Где
.
Выполним ряд преобразований:
.
Окончательная формула:
.
На основе этой формулы можно сделать сразу несколько принципиальных выводов:
- На значение вероятности не влияют изменения времени стоянки и ожидания поездов, если общий интервал не меняется (рис.
6).

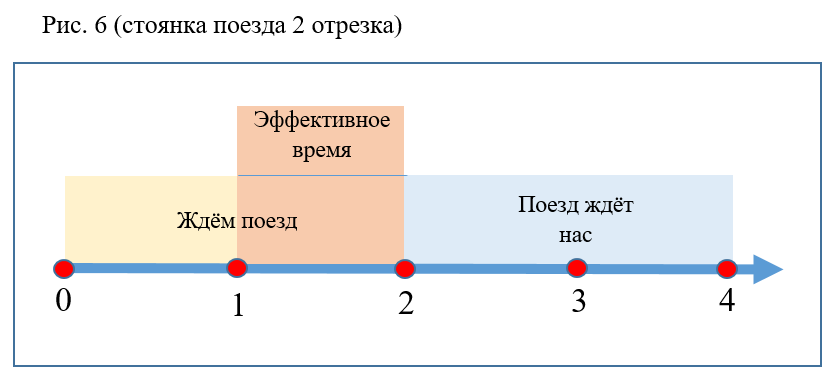
- Чем больше интервал между поездами, тем меньше вероятность P (рис.
7).
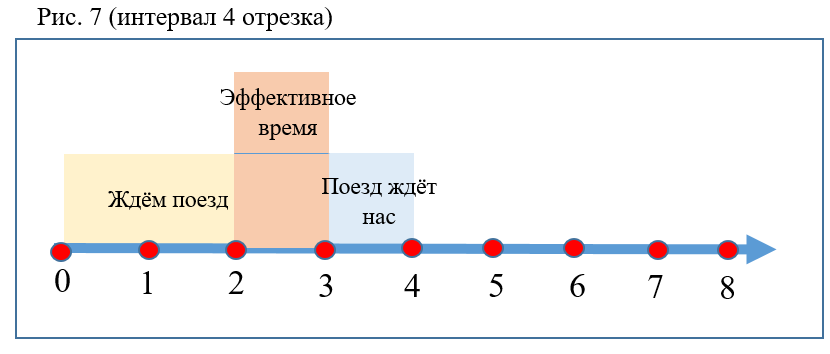

- Вероятность увеличивается, если увеличивается отношение времени спуска эскалатора к интервалу и/или коэффициент K.
Проверка верности
Теперь посмотрим, насколько верна выведенная формула? Чтобы проверить правильность формулы, обратимся к статистике, которую очень полезно собрал корреспондент The Village еще в 2014 году.Выражаю благодарность и, естественно, в конце статьи оставлю ссылку на оригинал статьи.
Также хорошо, что статистика представлена в виде наглядной инфографики.
Ээксперимент 1. Станция метро Чеховская
Давайте посчитаем вероятность
.
Здесь
;
;
;
;
.
Полученный результат, как видно, расходится с экспериментальными данными.
Формула неправильная? Нет! Из инфографики видно, что спуск на станцию предполагает поездку на двух эскалаторах, однако время перехода между ними не учитывается.
Если для надежности считать, что переход занимает не менее 30 секунд, то, подставив новое значение
мы получаем:
;
, что гораздо ближе к экспериментальному результату.
Также стоит отметить, что в эксперименте было всего 10 повторений.
Увеличивая количество повторений, можно добиться практически полного согласия расчетных данных с полученными в ходе эксперимента.
Эксперимент 2. Станция метро «Парк Победы».

Давайте посчитаем вероятность
.
Здесь
;
;
;
;
.
Видно, что мы получили вероятность больше единицы.
Но здесь нет противоречия.
Если посмотреть на общий вид формулы, то становится очевидным, что в случае, когда время спуска по эскалатору равно интервалу между поездами, то увеличение скорости хотя бы в 2 раза уже увеличит вероятность того, что ускоренный спуск эффективен, равен 0,5. Если время движения эскалатора больше интервала, то с тем же коэффициентом
вероятность успеть на поезд раньше только увеличится.
Наконец, если время спуска на эскалаторе в 2 и более раз превышает интервал, бегущий человек в 100% случаев успеет на поезд, который не успеет оставшийся на эскалаторе человек.
Именно такой эффект мы наблюдаем в этом эксперименте: корреспондент пришел к выводу, что в 10 из 10 случаев у него возникало желание бежать.
Эксперимент 3. Станция метро «Парк Культуры».

Давайте посчитаем вероятность
.
Здесь
;
;
;
;
.
Опять ошибка? Нисколько.
Видно, что, как сказано выше, время спуска по эскалатору в 2 раза превышает интервал между поездами.
Время спуска бегом в 2 раза меньше.
Получается, что каждый спуск должен быть эффективным.
Но не следует забывать, что прежде чем приступить к рассуждениям, мы приняли предположение о мгновенном закрытии дверей и не менее мгновенном отправлении поезда со станции.
Если представить себе такой вариант, как на рисунке 8, то станет понятно, что в реальной жизни бегущий человек может слегка пропустить посадку в пункте 1 (например, поезд уйдет немного раньше), а в пункте 2, наоборот, Поезд немного задержится, и тогда в него сядет тот, кто не сбежал, вместе с человеком, опоздавшим на предыдущий поезд и сбежавшим.

Я предполагаю, что именно это и произошло в оба «неэффективных» раза.
Есть все основания утверждать, что с увеличением количества повторений эксперимента процент «эффективных» прогонов будет стремиться к 100%.
выводы
Теперь, когда на основе имеющихся экспериментальных данных нам удалось подтвердить правильность формулы, проанализируем ее и сделаем выводы.Так как в самом начале мы договорились, что будем считать решение о спуске целесообразным, если вероятность эффективного спуска будет больше или равна 0,5. То есть, буквально, если мы можем быть уверены, что хотя бы в половине случаев побежим не зря, то действительно стоит рискнуть и побежать, ведь если мы опоздаем, то практически ничего не потеряем.
На основании вышесказанного перепишем формулу вероятности следующим образом:
.
Интересно, что, как мы уже выяснили, бежать всегда имеет смысл, когда
.
В то же время верно и то, что если
, то как бы быстро вы ни бежали, вероятность попасть в поезд раньше меньше 0,5, так как очевидно, что
никогда не будет больше или равно 1.
Теперь посмотрим на скорость корреспондента.
В среднем она примерно в 2 раза превышает скорость эскалатора (время спуска в 2 раза меньше).
В целом эти данные совпадают с результатами моих собственных экспериментов (не вижу смысла их приводить).
Как правило, уже сложно развить скорость, при которой коэффициент К был бы равен хотя бы 3: на реальном эскалаторе много желающих сбежать и притом стоящих слева людей или своих вещей.
(сумки, чемоданы) могут вам мешать.
Означает,
, А
.
То есть решение об ускорении будет целесообразным только в том случае, если соотношение
не менее 1. И это возможно только тогда, когда время спуска по эскалатору не меньше интервала между поездами.
В реальном метро, где средний интервал между поездами составляет 2 минуты, не все станции могут похвастаться долгим спуском.
Как правило, даже в петербургском метро время движения эскалатора составляет около 1 минуты 30 секунд, то есть в 0,75 раза меньше интервала.
Отсюда следует вполне очевидный и важнейший принципиальный вывод: если вы точно знаете, что эскалатор на данной станции движется меньше интервала между поездами, то бежать по нему нецелесообразно.
P.S. Учтите, пожалуйста, тот факт, что данное задание не учитывает необходимость попасть в конкретный вагон.
Речь идет исключительно о том, чтобы попасть на платформу и затем сесть в поезд. Источник экспериментальных данных: Деревня .
Еще раз выражаю свою благодарность! Теги: #математика #теория игр #метро #теория вероятностей
-
Алгоритм Двоичного Поиска
19 Oct, 24 -
Самовоспроизводящийся Код.
19 Oct, 24 -
Русская Документация По Php?
19 Oct, 24 -
Шесть Принципов Создания Новых Вещей.
19 Oct, 24 -
Как Подняться В Небо И Стать Пилотом
19 Oct, 24 -
Как Часто Вы Читаете «Песочницу»?
19 Oct, 24


