Введение
- Моделирование транспортных потоков стало одной из ведущих задач науки практически с момента появления первых автомобилей.
Считается, что основоположником этой отрасли является учёный из царской России Дубелир с его книгой «Городские улицы и тротуары» (1912).
За 100 лет непрерывных исследований было разработано множество хороших моделей, которые сегодня помогают строить качественные и быстрые дороги.
Но если вы думаете, что нерешённых вопросов не осталось, вы сильно заблуждаетесь, ведь светлые умы нашей планеты до сих пор ломают голову над решением проблем, о которых иногда задаются даже дети.
Например, как настроить светофор, чтобы вокруг него не было пробок?
Самый короткий путь
- Как нетрудно догадаться, дорожную сеть обычно представляют в виде график .
Несмотря на то, что большинство дорог двусторонние, существуют и участки с односторонним движением, что означает график ориентированный .
Для облегчения понимания будем считать, что график связанный , а именно, что из любой вершины графа всегда можно попасть в любую другую.
Представим себе такую ситуацию: две пустые дороги с одинаковым покрытием ведут из города А в город Б, какую из них лучше выбрать? Правильный ответ: какой короче.
Итак, счет приостановленный , поскольку каждому ребру можно присвоить номер, например, равный длине соответствующей дороги.
Такая система будет выглядеть примерно так.
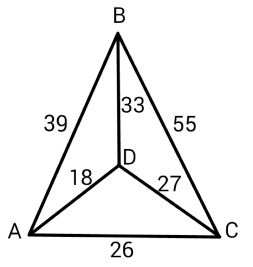
- Но если бы все было так просто, компании не тратили бы огромные суммы на разработку продвинутых навигаторов.
А все потому, что есть скоростные магистрали, а есть сельские грунтовые дороги, есть узкие городские улочки, есть МКАД.
Ну и соответственно основная проблема выбора правильного маршрута – пробки.
Вместо того, чтобы писать над краями кучу характеристик, обычно пишут функцию, а именно зависимость времени проезда участка дороги от количества машин.
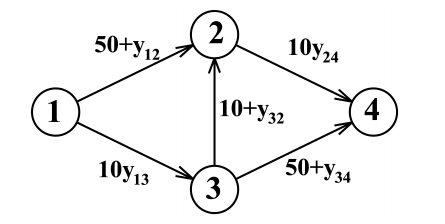
На этой диаграмме
- количество автомобилей, проезжающих через выбранное сечение в единицу времени в промежутке между городами 1-2
Максимальный поток
- Теперь перейдем к роли генерального плана города.
Вы хотите узнать, насколько хороша ваша дорожная сеть.
Чаще всего нужно узнать, сколько автомобилей одновременно могут передвигаться по той или иной магистрали.
Во время Второй мировой войны ВВС США были очень заинтересованы в том, как быстро и сколько войск можно будет перенаправить в критические боевые точки.
Решение проблемы нашел математик Джордж Бернард Данциг.
Пусть емкость ребра — это максимальная интенсивность потока, проходящего через ребро.
А насыщенная грань — это грань, по которой проходит максимальный поток.
Присвоим каждому разделу пару номеров (
,
).
— достигнутый пока поток по ребру сначала равен нулю, затем это число будет только увеличиваться, пока не достигнет
, объем ребер.На данный момент, по крайней мере, на одном маршруте из
все ребра ненасыщены (т.е.на всех ребрах
<
), цикл продолжается.1. Ищем любой участок маршрута, содержащий только ненасыщенные ребра из
В
.Если мы не можем найти аналогичный раздел, то цикл останавливается; максимальный поток, который мы пытаемся найти, представляет собой сумму потоков ребер, приходящих в
.2. Мы нашли дополнительный маршрут. Определение значения максимального расхода
, который мы можем пропустить по этому маршруту.Она определяется как минимальная из всех возможных разностей емкостей.
и существующий поток c по всем краям маршрута.3. Каждый
загнуть край с помощью
, таким образом, по крайней мере один край преобразуется в насыщенный.4. Вернитесь к (1.)
Микроскопическая модель
- В первых двух параграфах описывалась макроскопическая модель, но с 1950-х годов учёные стали рассматривать микроскопическую модель.
Основное отличие состоит в том, что поток рассматривается не как единое целое, а как каждый автомобиль в отдельности.
- Микроскопические модели транспортных потоков предполагают, что ускорение конкретного транспортного средства зависит от соседних транспортных средств.
Наибольшее влияние на поведение водителя оказывает автомобиль, движущийся впереди (лидер).
- Эта модель сложна и неоднозначна, поэтому ученые до сих пор пишут статьи, в которых предлагают все более совершенные функции, описывающие движение автомобилей, но чем совершеннее формула, тем она становится больше и сложнее.
Предпочтения пассажиров
- Представьте, что у вас большой таксопарк и вы пытаетесь понять, сколько машин оптимально иметь, по какой политике принимать заказы и кому именно звонить?
- Самый простой алгоритм перераспределения — ничего не делать, а когда потенциальный клиент подойдет к остановке, отправить к нему ближайшую свободную машину.
А что, если к этому месту уже приближается машина с пассажиром, которому нужно выйти? Значит, таксиста мы послали зря.
Поэтому надо учитывать и те машины, которые уже направляются на нашу станцию.
- Следующий важный вопрос — как построить так называемый эвристический алгоритм? Эvistic — это алгоритм, который каким-то образом использует некоторые вероятности из будущего.
Например, мы знаем, что скоро на станцию прибудет поезд, и многие пассажиры выйдут и захотят взять такси.
Может, стоит заранее отправить туда машины? Если да, то насколько заранее и сколько машин? Один из алгоритмов задает для каждой станции определенный индекс в зависимости от уже стоящих пассажиров, от некоторой статистики будущих прибытий и от расположения машин в системе.
Перекресток
- Пусть дано пересечение следующего типа:
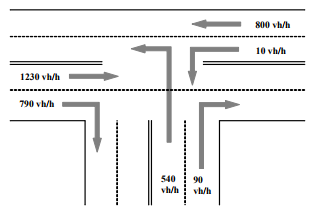
На рисунках представлена интенсивность потока в час пик и схема работы перекрестка.Какова оптимальная продолжительность фаз светофора (чтобы количество машин на перекрестке было минимальным)?
- Думаю, многие заметили, что большинство перекрестков никак не используют информацию о потоках транспортных средств и установленные на них длительности фаз светофора близки к случайным.
Многие предложат сделать длительность фаз пропорциональной потоку в каждом направлении.
Но это может привести к образованию длительной пробки в одном направлении.
Ээффективное решение, вполне очевидное.
- Пусть поток транспорта на шестиполосной дороге достигает Т-образного перекрестка.
И пусть цель трети водителей — повернуть налево, а цель остальных — продолжить движение.
Вы не можете поворачиваться и двигаться прямо одновременно (см.
рисунок).
В этом случае две левые полосы будут заняты водителями, желающими повернуть налево.
Сложная математическая модель ответит, почему водители будут занимать именно две полосы движения.
Поток транспортных средств через светофор при включении зеленого сигнала для прямого движения будет не теоретически возможным максимумом для данного количества полос (6000 автомобилей/час), а всего лишь 4000 автомобилей/час.
Это значит, что на этом участке вам нужно не 6 полос, а всего 4.

-
Почему Node Africa Выбрала Nsx
19 Oct, 24 -
Невский Экспресс – Терроризм Или Халатность?
19 Oct, 24


