Принято считать, что двумя основными операциями «машинного обучения» являются регрессия и классификация.
Регрессия – это не только инструмент выявления параметров связи y(x) между рядами данных.
Икс И й (которому я уже посвятил несколько статей ), но и частный случай их техники сглаживания.
В этом примере мы пойдем немного дальше и рассмотрим, как можно сделать сглаживание, когда тип зависимости y(x) заранее неизвестен, а также как можно отфильтровать данные, которые контролируются разными эффектами с существенно разным временем характеристики.
Одним из самых популярных алгоритмов сглаживания, используемых, в частности, в биржевой торговле, является скользящее усреднение (включаю его в цикл статей по машинному обучению с некоторой натяжкой).
Рассмотрим скользящее усреднение на примере колебаний курса доллара за последние несколько недель (опять же используя Маткад ).
Сами расчеты врут Здесь .
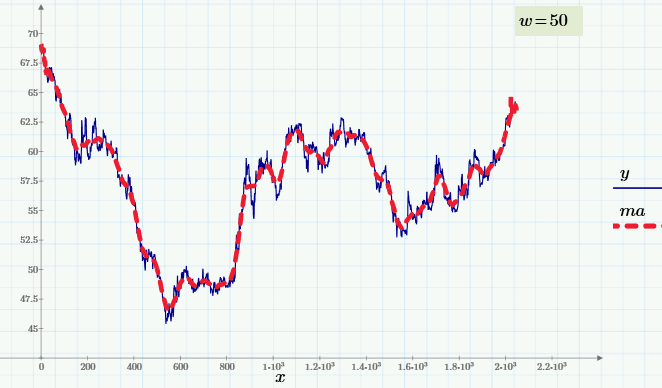
На графике ниже показан курс доллара к рублю с интервалом в 1 час.
Исходные данные представлены синей кривой, а сглаженные данные представлены красной кривой.
Даже невооруженным взглядом видно, что колебания валютного курса имеют несколько характерных частот, что является предметом одного из направлений технического анализа рынков.
Сглаживание с использованием скользящей средней Принцип сглаживания, основанный на «скользящее среднее» (МА — от англ.
«скользящее среднее») состоит из вычислений для каждого значения аргумента y я среднее значение из соседних w данных.
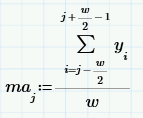
Число w называется окно скользящее усреднение: чем оно больше, тем больше данных участвует в вычислении среднего, соответственно, тем более плавной получается кривая.
На верхнем рисунке окно w=50, но вот как будет выглядеть скользящее усреднение при w=200. 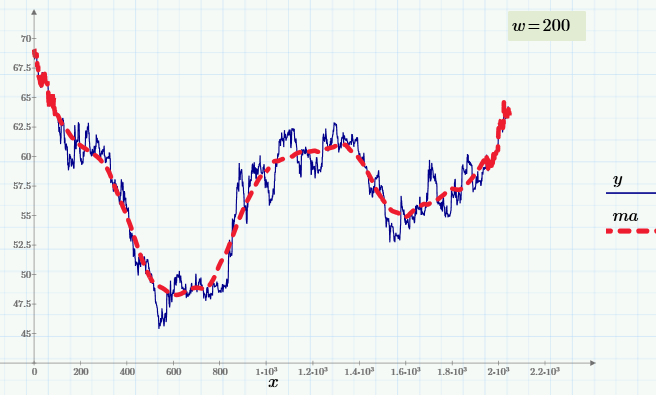
Как изменяется спектр Фурье данных во время скользящего среднего?
Очевидно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w отражают лишь характер их медленных изменений.
Это типичный пример фильтрации данных, т.е.
исключения одной из составляющих зависимости y(x я ).
Наиболее распространенной целью фильтрации является подавление быстрых изменений y(x я ), которые обычно вызваны шумом.
В результате из быстро осциллирующей зависимости y(x я ) получается другая, сглаженная зависимость, в которой доминирует низкочастотная составляющая.
Эти рассуждения плавно подтолкнули нас к терминологии спектров.
Нарисуем график преобразования Фурье ( «Фурье-спектр» ) источник данных: 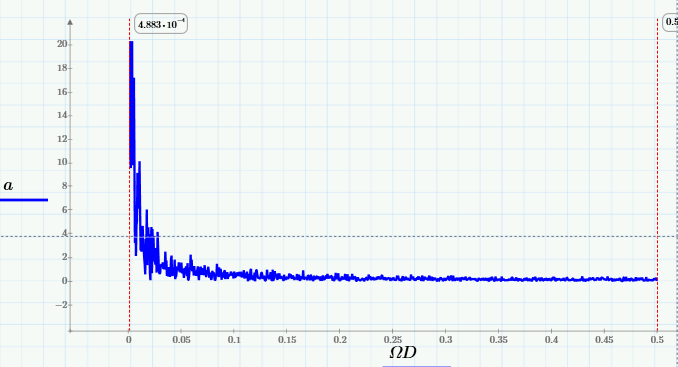
и убедиться, что спектр скользящего среднего отсекает от него высокие частоты (начиная примерно с 0,005 Гц): 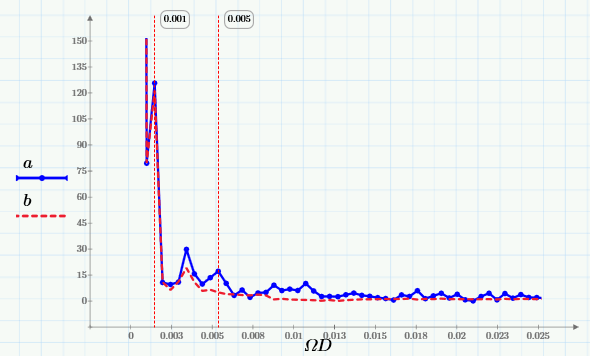
Пояснение: Спектр Фурье суммы синусов и ее MA.
Чтобы объяснить принцип расчета спектра Фурье, вместо (случайных) исходных данных рассмотрим простую модель суммы нескольких детерминированных сигналов (синусоидальных волн с разными частотами и амплитудами) и псевдослучайного шума: 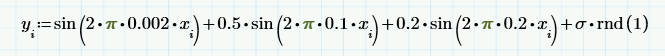
Вот графики этой суммы и ее MA (с тем же окном w=200): 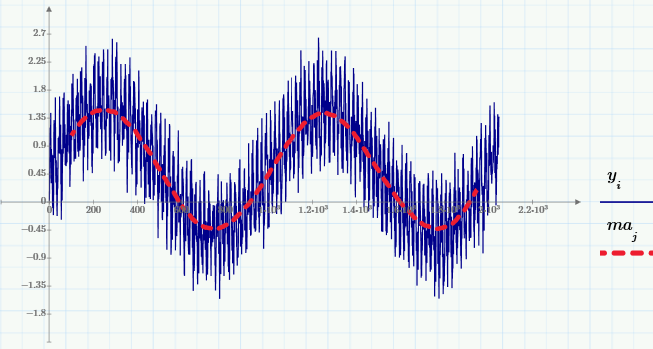
а также их спектры Фурье: 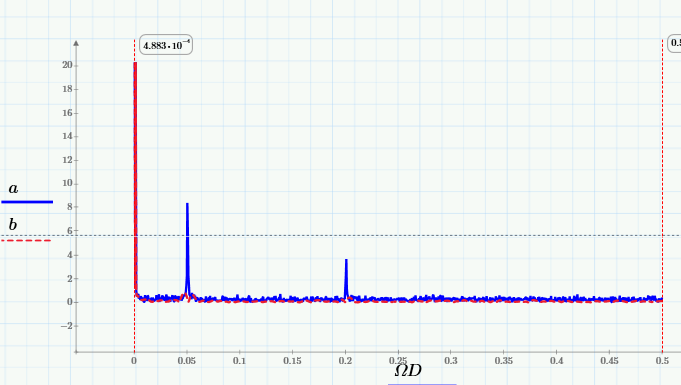
По ним видно, что скользящее усреднение отсекает из сигнала высокие частоты, начиная с частоты 0,005 Гц.
Лучше это видно на крупном плане низкочастотной области спектра: 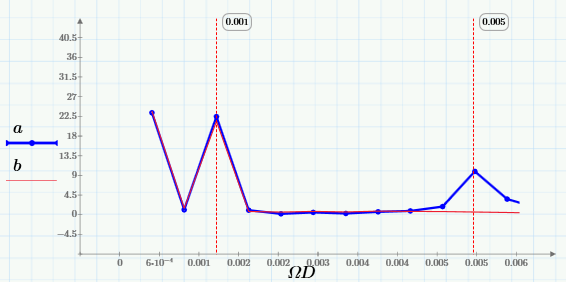
Таким образом, выбрав подходящее окно, можно сдвинуть область подавленных частот в нужном направлении (чем больше w, тем дальше эта граница смещается влево).
Полосовая фильтрация Вернемся к биржевой аналитике и продемонстрируем предельно простой метод вырезания необходимой полосы частот из исходных данных.
А именно, в отличие от подавления шума (высокочастотной составляющей) часто рассматривается противоположная задача – устранение медленно меняющихся вариаций (иногда эту задачу называют устранение тенденции , или снижение тренда ).
Используя скользящее усреднение, реализовать это очень просто – вычитая MA из сигнала (при выбранном окне): 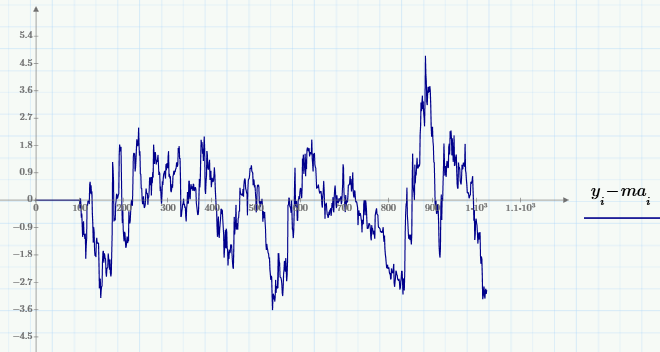
Интерес представляют также смешанные задачи выявления среднемасштабных вариаций путем подавления как более быстрых, так и медленных вариаций.
Одно из возможных решений предполагает использование «полосовая фильтрация» , который реализуется следующим образом: 1. Устранение высокочастотной составляющей из сигнала y, с целью получения сглаженной середины сигнала, например, с помощью скользящего усреднения с небольшим окном (например, w = 200).
2. Выделение медленной низкочастотной составляющей от середины сигнала, например, путем скользящего усреднения с большим окном w. 3. Вычитание медленного тренда из середины сигнала, тем самым выделяя среднемасштабную составляющую исходного сигнала y. Я оставляю возможность заинтересованному читателю реализовать полосовую фильтрацию в Маткад Экспресс (с небольшой оговоркой, что в бесплатной версии Маткады отключен алгоритм БПФ расчета спектров Фурье, и поиграться с ним не получится).
Сами расчеты Здесь .
Литература: 1. Кирьянов Д.
В.
, Кирьянова Е.
Н.
Вычислительная физика ( PDF , глава 1, пункты 6 и 7).
М.
: Полибук Мультимедиа, 2006. 2. Бат М.
Спектральный анализ в геофизике.
М.
, Наука, 1980. Теги: #фильтр #спектр #bpf #Фурье #полосовая фильтрация #скользящее среднее #.
Ma #скользящее среднее #курс доллара США #тренд #математика #машинное обучение

-
Некоторые Факты О Планшете Google Android
19 Oct, 24 -
Базовая Настройка Серии Juniper Srx
19 Oct, 24 -
Алтнет Официально Вышел На Российский Рынок
19 Oct, 24


