Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции.
Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном представлении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела.
Природа угловой скорости
- Окончательное вращение твердого тела.
Свойства тензора вращения и как его рассчитать
- О свертках тензора Леви-Чивита
- Вывод тензора угловой скорости через конечные параметры вращения.
Используем голову и Максиму
- Получаем вектор угловой скорости.
Работаем над недостатками
- Ускорение точки тела при свободном движении.
Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Максима в задачах преобразования тензорных выражений.
Угловая скорость и ускорение в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Скетч про орех Джанибекова
- Математическое моделирование эффекта Джанибекова
Однако численное моделирование – тоже очень интересный вопрос, особенно тот, который входит в круг моих исследовательских задач.
Поэтому сегодня мы
- Давайте наконец определимся, как использовать параметры Родрига-Гамильтона для описания ориентации тела в пространстве.
- Рассмотрим формы представления уравнений движения свободного тела: покажем, как тензорные уравнения можно превратить в матричные и компонентные.
- Смоделируем движение свободного твердого тела при различных соотношениях главных моментов инерции и покажем, как проявляется эффект Джанибекова.
Векторная форма записи удобна для общего анализа характера зависимостей; оно знакомо и в нем ясно, что означает тот или иной термин.
Однако для дальнейшего преобразования уравнений к виду, удобному для моделирования, перейдем к тензорным обозначениям
Где
— контравариантные координаты центра масс тела;
— контравариантные компоненты главного вектора внешних сил, приложенных к телу;
- контравариантные составляющие главного момента внешних сил, приложенных к телу.
Система уравнений (2) уже замкнута; проинтегрировав его, можно получить закон движения центра масс и зависимость угловой скорости тела от времени.
Но, нас будет интересовать еще и ориентация тела, поэтому дополним эту систему уравнений
Уравнение (3) представляет собой не что иное, как представление компонент угловой скорости через параметры ориентации Родрига-Гамильтона.
Мы уже получили это выражение в предыдущих статьях .
Будем теперь рассматривать его как дифференциальное уравнение, связывающее параметры ориентации с компонентами угловой скорости.
Однако параметры Родрига-Гамильтона избыточны — их четыре, а для описания ориентации тела в пространстве достаточно трех координат. А количество неизвестных в системе (2), (3) превышает количество уравнений на одно.
Это означает, что нам придется дополнить уравнения (2) и (3) уравнением связи между параметрами ориентации.
В статья о параметрах Родрига-Гамильтона мы показали, что вращение тела удобно описывать единичным кватернионом, т.е.
или в тензорной форме
Продифференцируем (4) по времени
Учитывая коммутативность скалярного произведения, полагаем
, Затем
и – искомое уравнение связи.
Полная система уравнений движения свободного твердого тела в тензорной форме будет иметь вид
Довольно страшно — (6) содержит 13 нелинейных дифференциальных уравнений первого порядка с 13 неизвестными величинами.
Это выглядит устрашающе из-за общей тензорной записи, но при переходе к конкретным координатам, в нашем случае декартовым, система (6) существенно упростится.
2. Матричная форма дифференциальных уравнений движения твердого тела в декартовом базисе
Введем вектор-столбец фазовых координат тела
Где
И
— положение и скорость центра масс тела;
И
— ориентация и угловая скорость тела.
В декартовом базисе метрический тензор представляется единичной матрицей, а символы Кристоффеля равны нулю, поэтому система уравнений (6) в матричной форме запишется следующим образом
куда вводятся матрицы
Разрешая систему (7) по первым производным, получим
система уравнений движения в форме Коши.
3. Моделирование эффекта Джанибекова
В отсутствие внешних силовых факторов правая часть системы (8) равна нулю, и уравнение движения центра масс легко интегрируется с учетом начальных условий
Вращение гайки описывается системой семи уравнений первого порядка, которую мы получаем из (8) введением безразмерных моментов инерции
И
Для численного интегрирования системы (9) зададим начальные условия
Где
— угловая скорость гайки после схода с резьбы;
— начальное возмущение угловой скорости
Со значениями параметров
, рад/с,
, рад/с, гайка движется следующим образом Параметры ориентации Родрига-Гамильтона 
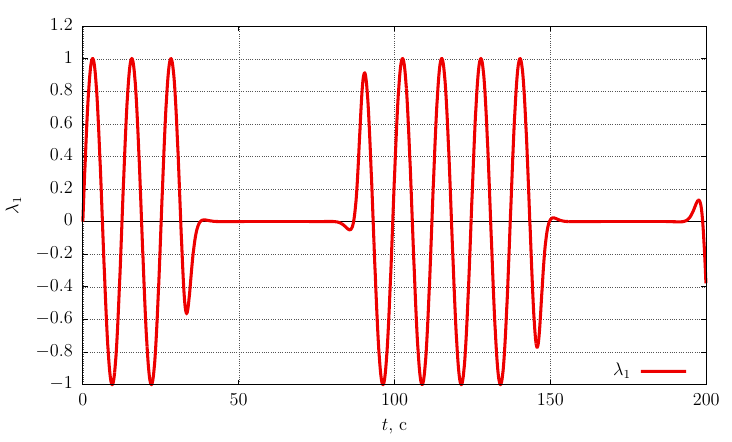
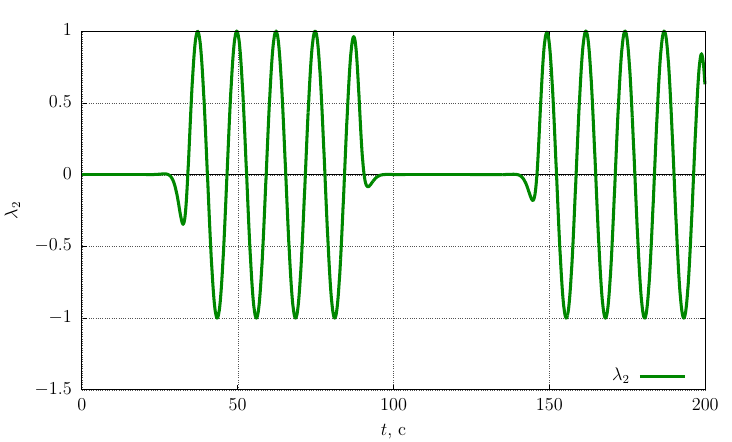
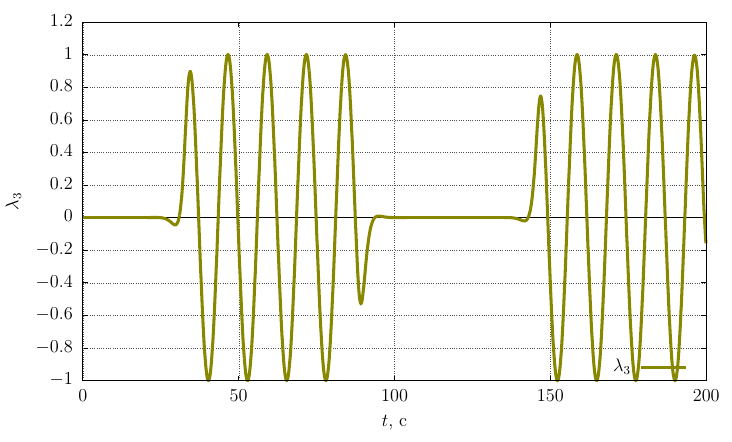
Проекции угловой скорости на свои оси 
Из графиков видно, что когда
, очень незначительное возмущение вектора угловой скорости приводит к периодическому лавинообразному изменению ориентации гайки в пространстве.
Сравним полученный результат с движением тела, закрученного вокруг оси с максимальным моментом инерции, т. е.
положим
установив следующие значения параметров
, рад/с,
, рад/с Параметры ориентации Родрига-Гамильтона 
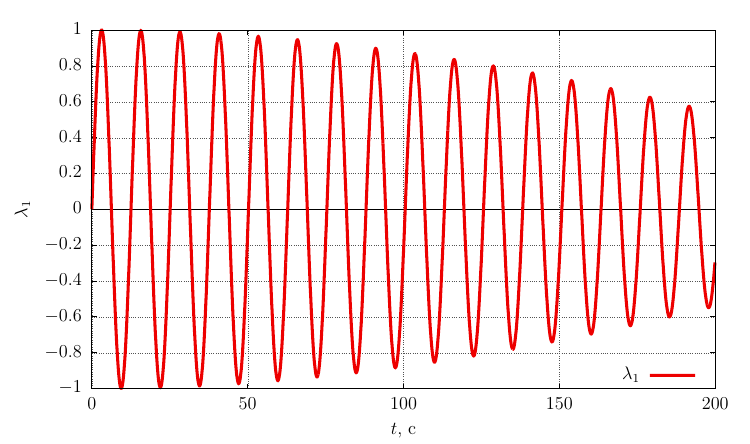
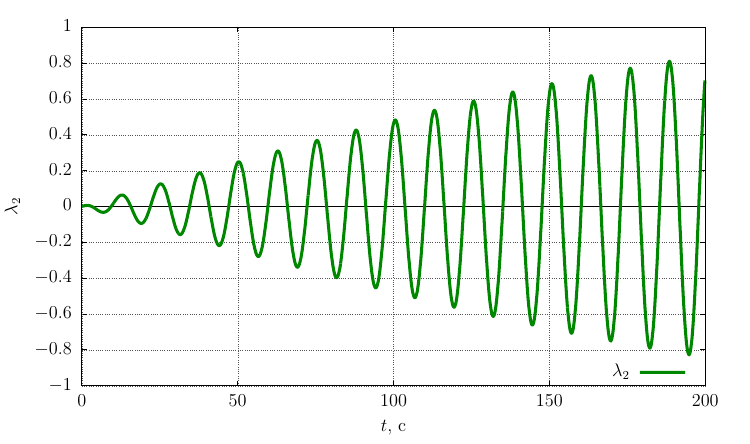

Проекции угловой скорости на свои оси 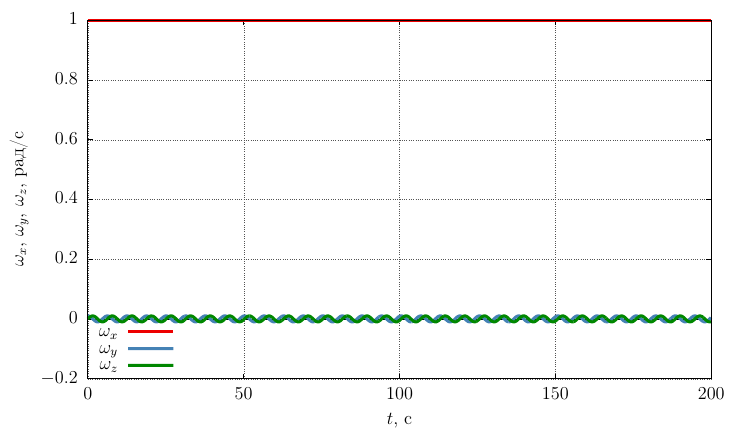
Видно, что при достаточно значительном возмущении угловой скорости движение сохраняет устойчивое вращение вокруг оси.
с небольшой прецессией.
Аналогичная картина наблюдается и для тела, закрученного вокруг оси с минимальным моментом инерции (
)
, рад/с,
, рад/с Параметры ориентации Родрига-Гамильтона 



Проекции угловой скорости на свои оси 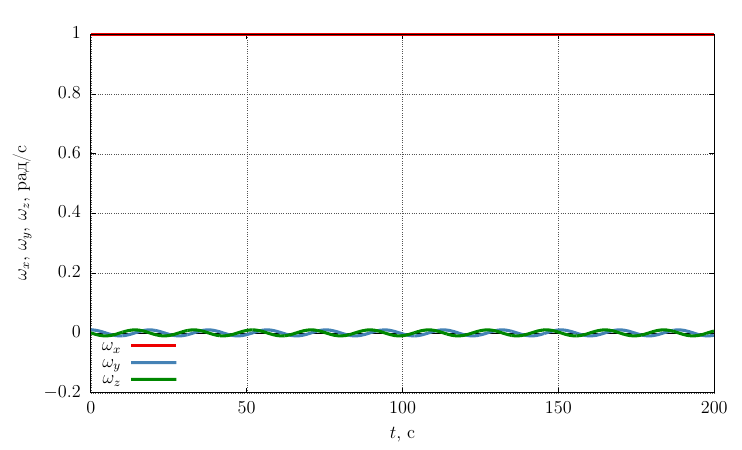
Частота прецессии существенно меньше, чем при вращении вокруг оси с максимальным моментом инерции, что логично, так как колебания происходят вокруг оси с большим моментом инерции, чем в случае
.
Заключение Все расчеты выполнены автором в SKA Maple 18. Графики построены по журналу расчетов с помощью комбинации Kile+LaTeX+gnuplot. Еще хотелось бы сделать анимацию, но опыт автора в этом деле крайне мал.
Поэтому хотелось бы задать читателям вопрос: существует ли программное обеспечение (для Linux/Windows), с помощью которого по заданному набору значений параметров кватерниона ориентации в зависимости от времени можно сделать анимационный видеоролик, иллюстрирующий движение тела ? Я подозреваю, что нечто подобное можно сделать с помощью Blender 3D, но я не уверен.
А пока спасибо за внимание! Обновить : Благодарности Однако совсем забыл написать, что эта статья (и предыдущая) подготовлена с помощью веб-приложения.
Редактор Markdown и LaTeX созданный пользователем парпалак .
Эта система позволяет набирать тексты статей в Макдауне и LaTeX и генерирует код, пригодный для непосредственной вставки в редактор Хабра.
Я благодарен автору за участие в тестировании продукта.
С его разрешения рекомендую данную систему к использованию при подготовке математических текстов статей.
Продолжение следует… Теги: #эффект Джанибекова #свободное движение тела #устойчивость движения #моделирование #параметры Родрига-Гамильтона #математика
-
Все О Ноутбуке Lenovo Ideapad G530 4151-A2U
19 Oct, 24 -
Великобритания Наконец-То Перешла На Voip
19 Oct, 24 -
Фильтр Введенных Во Вход Символов
19 Oct, 24 -
3 Книги По C++17 (На Английском Языке)
19 Oct, 24


